3.6 Методи апроксимації случайных сигналов

3.6.1 Вейвлети

Подання випадкових сигналів та зображень у вигляді ряду чи перетворень Фур’є є малоефективним. Це пов’язано з тим, що базисна функція рядів Фур’є – синусоїда – визначена у проміжку з дота за своєю природою є гладкою періодичною функцією. Більш ефективним рішенням є вибір принципово нового базису та класу функцій-вейвлетів, які використовуються для декомпозиції та реконструкції функцій та сигналів, у тому числі нестаціонарних.Вейвлети (wavelets) – це узагальнена назва особливих функцій, які мають вигляд коротких хвильових пакетів з нульовим інтегральним значенням та з тією чи іншою, іноді дуже складною, формою. Такі функції локалізовані на осі незалежної змінної і здатні до зсуву по ній та масштабуванню (розтягнення/стиснення).

Вейвлети створюються за допомогою спеціальних базових функцій – прототипів, які задають їх вигляд та властивості та відповідають ряду специфічних умов. Набір вейвлетів, в їх часовому чи в частотному поданні, може апроксимувати складний сигнал чи зображення, причому ідеально точно чи з деякою похибкою.

Вейвлет-спектрограми найбільш інформативні, ніж звичайні Фур’є- спектрограми, та на відміну від останніх, дозволяють легко виявити надтонкі локальні особливості функцій, сигналів та зображень.

Порівнюючи з тригонометричними базисними функціями (ряд Фур’є), які найбільш локалізовані в частотній зоні, але зовсім не локалізовані в часовій зоні, а також з деякою імпульсною базисною функцією (функцією Кронекера), яка чітко локалізована в часової зоні, але зовсім не несе ніякої інформації про частоту сигналу, вейвлети займають проміжне положення та характеризуються своїм часовим (рис. 3.14) та частотним образами (рис. 3.15). Часовий образ визначається деякою функцією часу (psi-функцією). Частотний образ визначається функцією-образом (Фур’є-образом), який задає обвідну спектра вейвлета. Фур’є-образ визначається виразом:.

Для демонстрації цих параметрів зручно використовувати вейвлет типу «мексиканський капелюх». Його часовий образ, на відміну від більшості інших вейвлетів, описується аналітичним виразом .

Очевидно, що зазначений вейвлет нагадує згасаюче синусоїдне коливання з деякою «середньою частотою» та площиною (над віссю часу та під нею) близькою до нуля. Точне нульове значення площини (над віссю часу та під нею) – одна з важливіших умов, яка дозволяє віднести часову залежність до вейвлет. Якщо вейвлет у просторі звужується, його «середня частота» підвищується, спектр вейвлета переміщується в зону більш високих частот та розширюється.

Існує велика кількість різновидів вейвлетів, які відрізняються як за формою так і за кількістю базисних коефіцієнтів. Приклади найбільш уживаних вейвлет-функцій наведено на рис. 3.16.

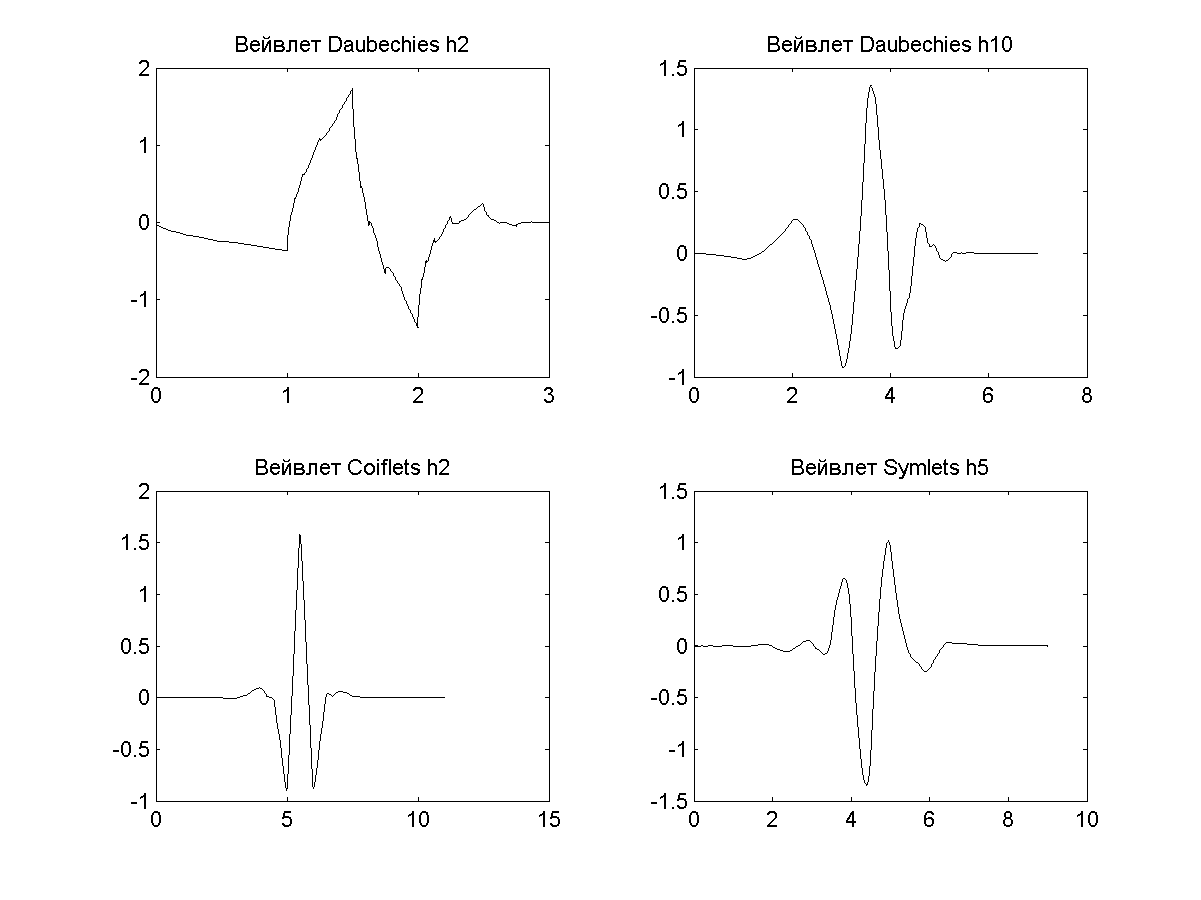
Рис. 3.16 Приклади найбільш уживаних вейвлет-функцій

З допомогою вейвлетів сигнал подається сукупністю хвильових пакетів – вейвлетів, утворених на основі повної початкової (базової) функції . Ця сукупність, різна в різних частинах часового проміжку визначення сигналу та коректована множниками, іноді має вигляд складних часових функцій, та подає сигнал з тим чи іншим ступенем деталізації. Такий підхід має назвувейвлет-аналізом сигналів.

Кількість вейвлетів, які використовуються в процесі розкладення сигналу, задає рівень декомпозиції сигналу. За нульовий рівень декомпозиції частіше за все приймають сам сигнал, а наступні рівні декомпозиції утворюють вейвлет-дерево того чи іншого вигляду. Точність подання сигналу під час переходу на нижчій рівень декомпозиції знижується, проте з’являється можливість вейвлет-фільтрації сигналів, вилучення шумів та ефективної компресії сигналів. Іншими словами стає можливою вейвлет-обробка сигналів.

Одна з ґрунтовних ідей вейвлет-подання сигналів полягає у розподіленні на дві складові наближення до сигналу: грубу (апроксимуючу) та уточнюючу (деталізуючу), з подальшим їх уточненням ітераційним методом. Кожний крок такого уточнення відповідає певному рівню декомпозиції та реставрації сигналу. Це можливо як у часовій, так і в частотній зонах представлення сигналів вейвлетами.

В основі неперервного вейвлет-перетворення НВП (або CWT – Continue Wavelet Transform) лежить використання двох неперервних та інтегрованих по всієї вісі (чи) функцій:

• вейвлет-функції 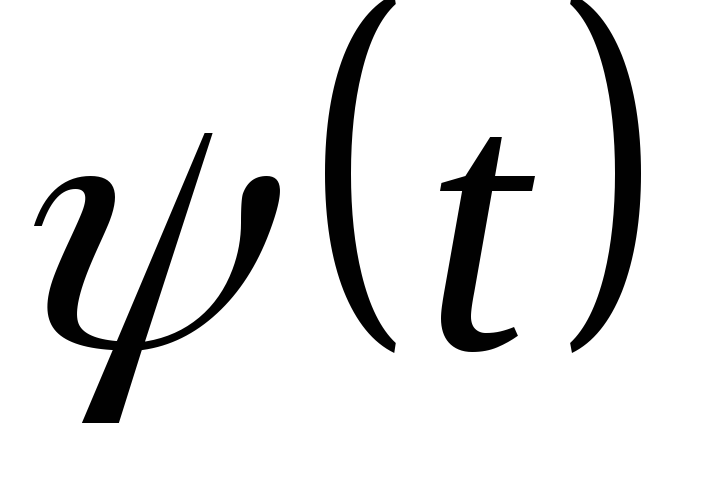з нульовим значенням інтеграла (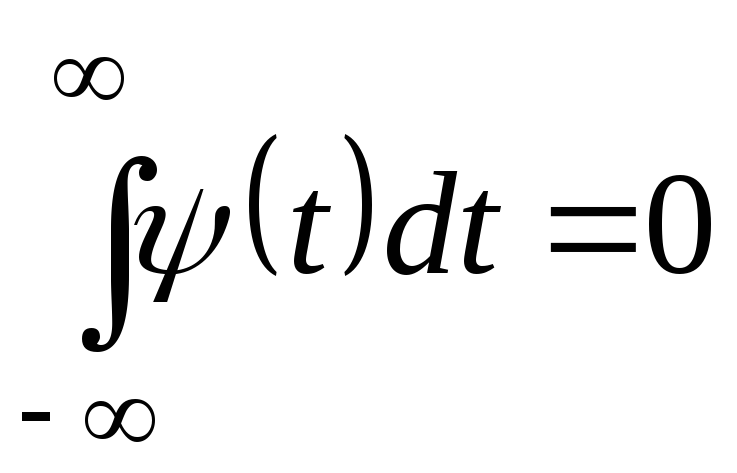), яка визначає складові сигналу та породжує деталізуючі коефіцієнти;

• масштабувальної або скрейлинг-функції 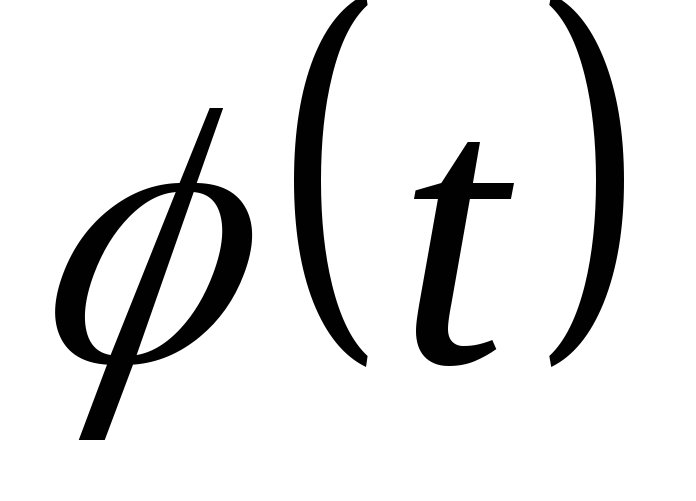з одиничним значенням інтеграла (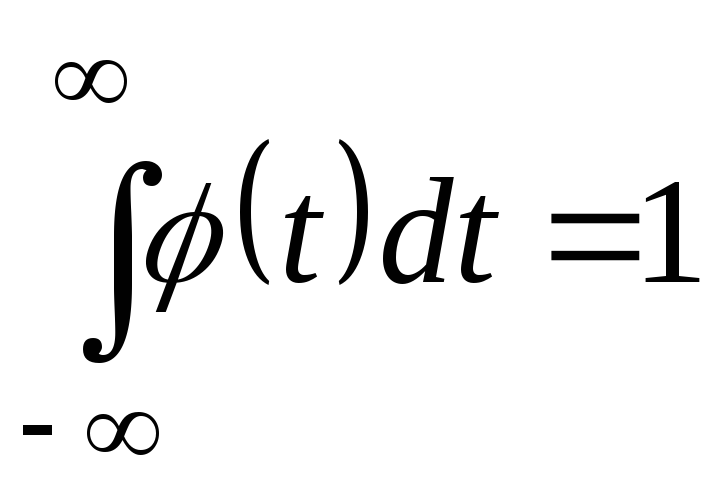), яка визначає грубе наближення (апроксимацію) сигналу та яка породжує коефіцієнти апроксимації.

Phi-функції притаманні далеко не всім вейвлетам, а тільки тим, які належать до ортогональних.

Psi-функція формується на основі тієї чи іншої базисної функції, яка як і, визначає тип вейвлета. Базисна функція має відповідати вимогам, визначеним для psi-функціїі забезпечувати виконання двох основних операцій:

• зсув по осі часу :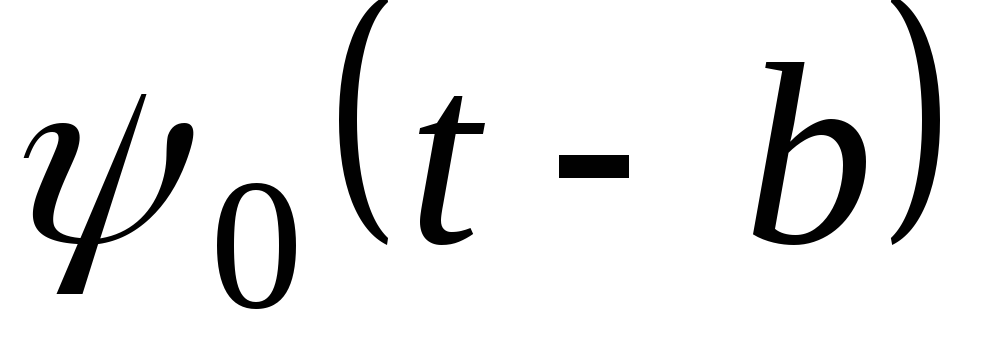при;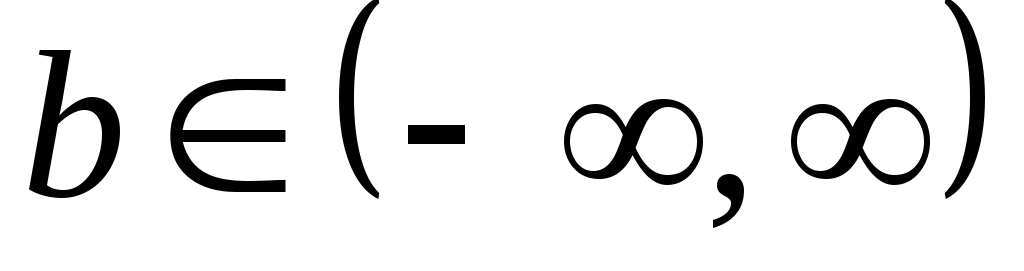

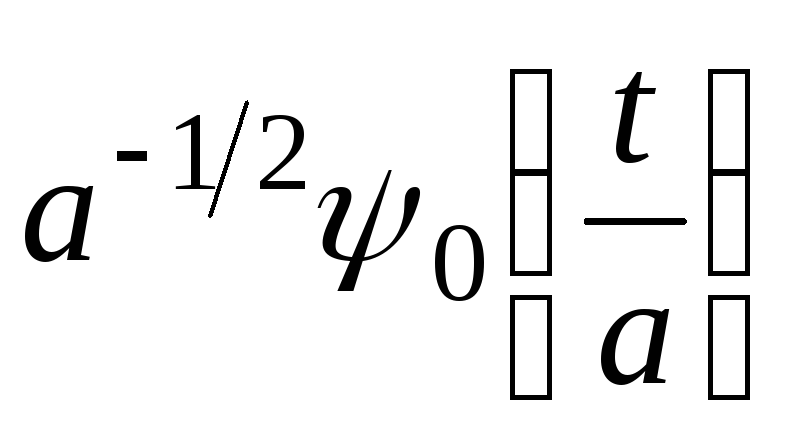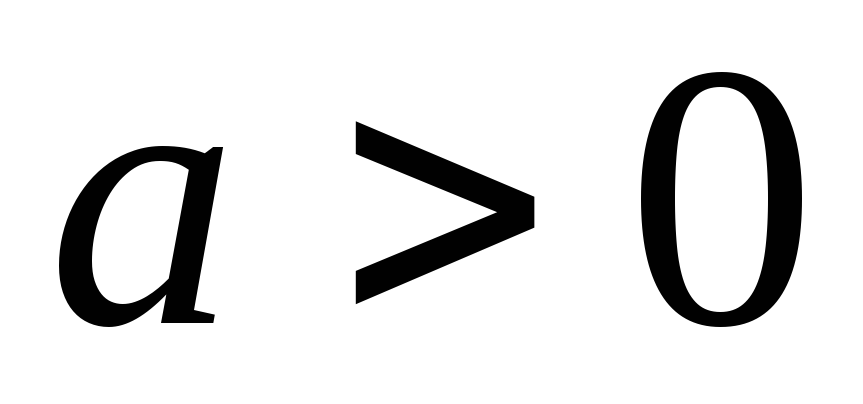• масштабування: прии.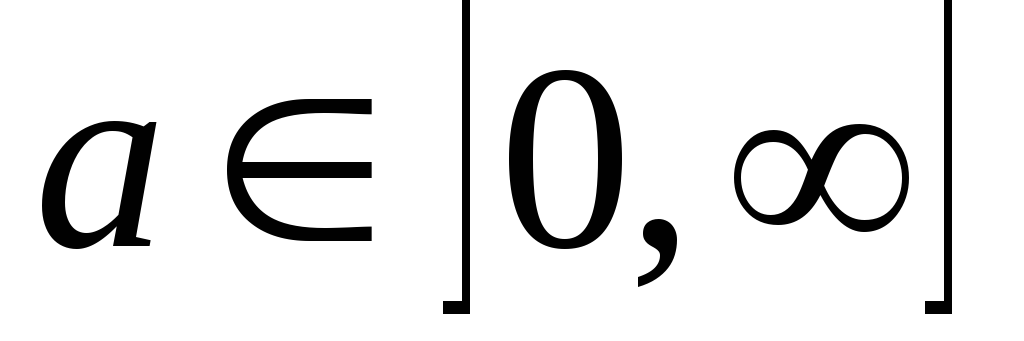

Параметр задає ширину цього пакета, а- його положення. Неважко впевнитися в тому, що наступний вираз задає водночас дві ці властивості функції:

.

Отже, для наведених тафункціяі є вейвлет. Вейвлети, позначені як, іноді називають «материнськими вейвлетами», оскільки вони породжують цілу низку вейвлетів певного виду. Про вейвлети, які чітко локалізовані в просторі (чи в часі), говорять, що вони мають компакстний носій.

Пряме неперервне вейвлет-перетворення (ПНВП) сигналу задається, за формальною аналогією з перетворенням Фур’є, шляхом обчислення вейвлет-коефіцієнтів за формулою:

,

де позначення означає скалярне перемноження відповідних множників, а границі інтегрування враховують обмеження.

Пряме вейвлет-перетворення можна розглядати як розкладання сигналу за всіма можливими зсувами та розтягнення/стиснення сигналу або деякої довільної функції. При цьому параметритаможуть набувати будь-яких значень в межах вказаних вище областей їх визначення. Зазначимо, що пряме перетворення Фур’є також можна розглядати як розкладення за зсувами (мається на увазі фазовий зсув гармонік, які задають положення їх графіків) та розтягнення/стиснення (які визначаються значеннями амплітуд гармонік), але стосовно до однієї функції (синусоїди), що не дуже зручно для акцентування локальних особливостей сигналів.

Обернене неперервне вейвлет-перетворення (ОНВП) здійснюється за формулою реконструкції в часової зоні:

,

де - константа, яка визначається тільки функцією.

Частотне (спектральне) подання вейвлетів має важливе значення для визначення фільтруючих властивостей вейвлет-перетворень та алгоритму швидкого вейвлет-перетворення (ШВП), який на них ґрунтується.

Відповідно до такого підходу частотна зона вейвлетів може бути розподілена на дві складові – низькочастотну та високочастотну. Їх частота розділення дорівнює половині частоти дискретизації сигналу. Для їх розділення достатньо використовувати два фільтри: низькочастотний та високочастотний, до входів яких подається сигнал. Фільтрдає частотний образ для апроксимації (грубого наближення) сигналу, а фільтр- для його деталізації.

Оскільки фільтри передають тільки половину всіх частотних компонентів сигналу, то компоненти, які не потрапили у смугу прозорості можна вилучити. Ця операція отримала назву «децимація».

Однак фільтр можна, в свою чергу, розкласти на два фільтри та знов піддати спектри цих нових фільтрів операції децимації. Це означає зміну рівня реконструкції. Таким чином, можна сформувати систему вейвлет- фільтрів, які реалізують операцію декомпозиції сигналу того чи іншого рівня.

Подібні операції врешті решт скорочують спектр відповідних компонентів сигналу і являють собою основу приблизного подання сигналу на різних рівнях його декомпозиції. Таке надання необхідне, наприклад, для реалізації операції стиснення сигналів та їх очищення від шуму. Операція послідовного «розклеювання» фільтрів та поступового огрубіння подання сигналу отримала назву алгоритму Малла (на честь французького вченого Mallat).