
- •Введение
- •1. Прямоугольная система координат на плоскости
- •2. Отрезок. Длина отрезка. Деление отрезка в данном отношении
- •3. Уравнение прямой в декартовых координатах
- •4. Взаимное расположение прямых на плоскости
- •5. Задания для самостоятельной работы
- •Заключение
- •Библиографический список
- •Прямая на плоскости
- •680021, Г. Хабаровск, ул. Серышева, 47.
4. Взаимное расположение прямых на плоскости
Прямые, находящиеся в одной плоскости, будут либо пересекающимися, либо параллельными. Выясним условия, при которых прямые соответствуют тому или иному случаю, определим угол между прямыми, координаты точки пересечения, если таковая имеется.
Пусть две прямые заданы уравнениями
![]() ,
,![]() .
(4.1)
.
(4.1)
Поскольку угловой коэффициент определяет наклон прямой к оси абсцисс, то очевидно, что равные углы наклона соответствуют параллельным прямым. Поэтому условием параллельности двух прямых, заданных уравнениями (4.1) является равенство их угловых коэффициентов
![]() .
(4.2)
.
(4.2)
Если
![]() ,
тоугол
,
тоугол
![]() между прямыми(4.1) определяется
известной тригонометрической формулой
тангенса разности двух углов
между прямыми(4.1) определяется
известной тригонометрической формулой
тангенса разности двух углов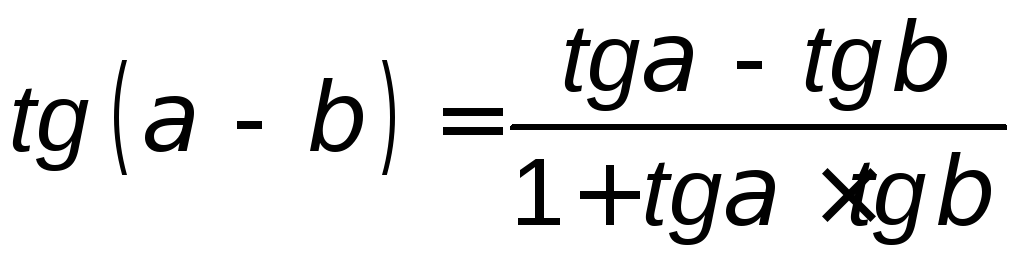 ,
которое в случае прямых принимает вид
,
которое в случае прямых принимает вид
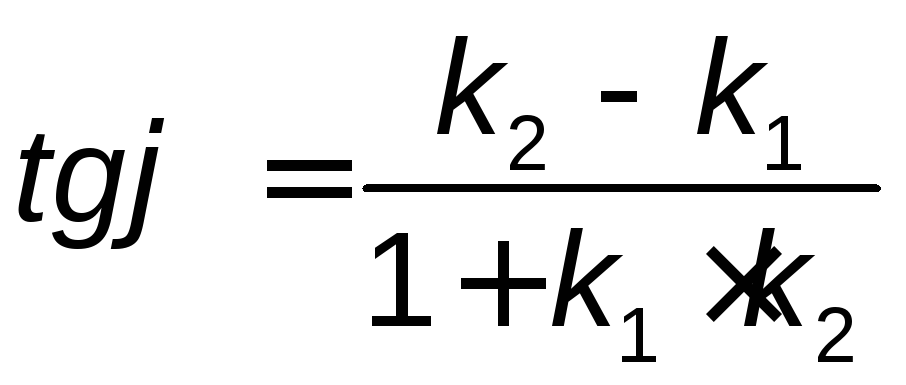 .
(4.3)
.
(4.3)
Если прямые (4.1) перпендикулярны,т.е.![]() ,
то
,
то
![]() − (4.4)
− (4.4)
условие перпендикулярности двух прямых.
Если прямые заданы общими уравнениями
![]() ,
,![]() ,
(4.5)
,
(4.5)
то указанные выше условия будут выглядеть так:
условие параллельности 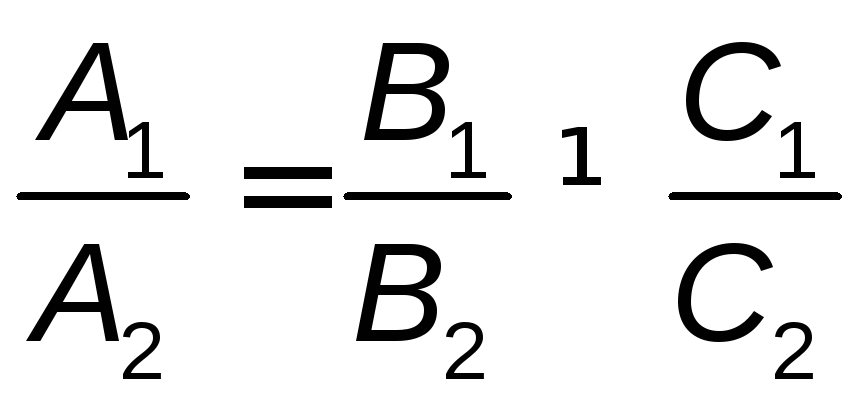 ;
(4.6)
;
(4.6)
условие перпендикулярности ![]() ;
(4.7)
;
(4.7)
угол между прямыми 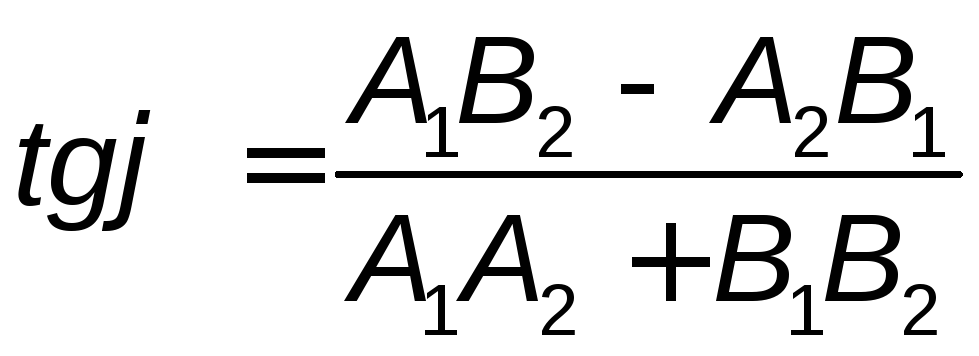 .
(4.8)
.
(4.8)
Условие
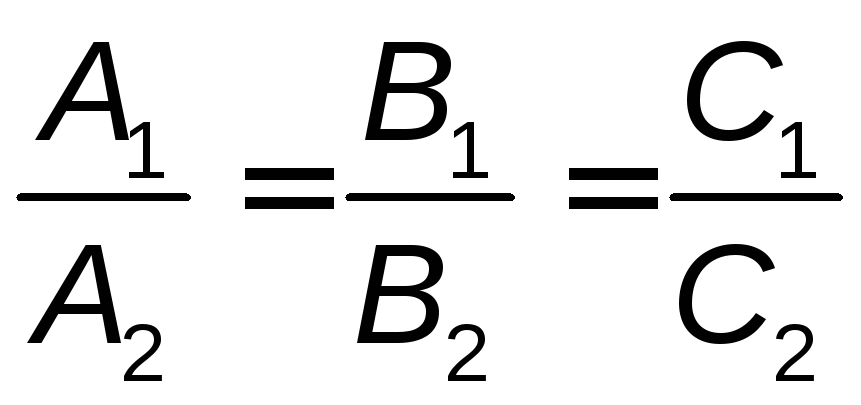 (4.9)
(4.9)
определяет совпадающие прямые.
Точка пересечения двух прямых(4.5) есть общая точка этих прямых. Координаты этой точки должны одновременно удовлетворять уравнениям обеих прямых, т.е. системе
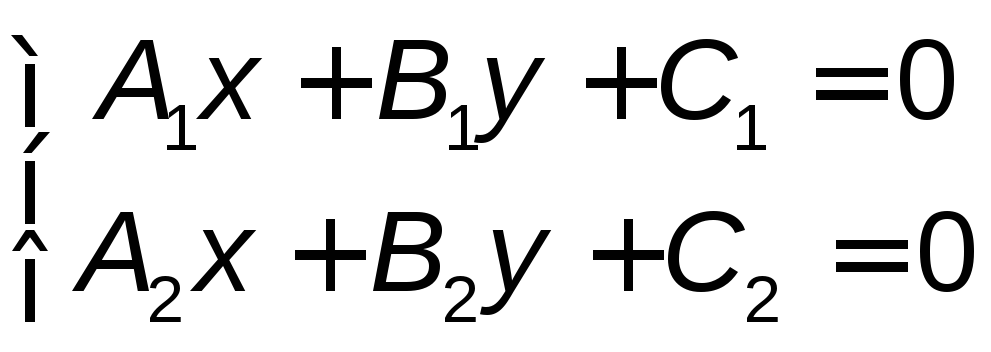 .(4.10)
.(4.10)
Решая эту систему, находим координаты искомой точки.
Замечание.Для определения угла между прямыми, удобнее переходить к уравнению с угловым коэффициентом.
Пример 1. Напишите уравнение медианы АМ треугольника АВС, если заданы координаты его вершин А(-5;4), В(3;1), С(2;-5).
Решение.Точка М − середина
отрезка ВС, поэтому в соответствии с
формулами (2.5)![]() ;
;![]() ;
М(2,5;-2). Уравнение прямой АМ запишем,
используя формулу (3.1):
;
М(2,5;-2). Уравнение прямой АМ запишем,
используя формулу (3.1):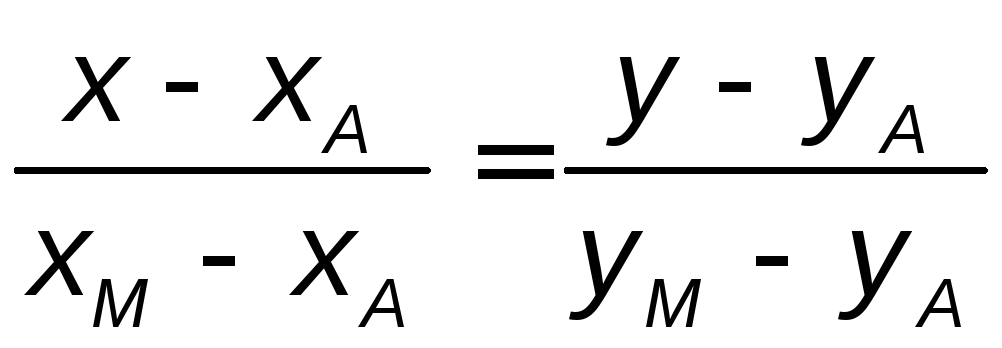 или
или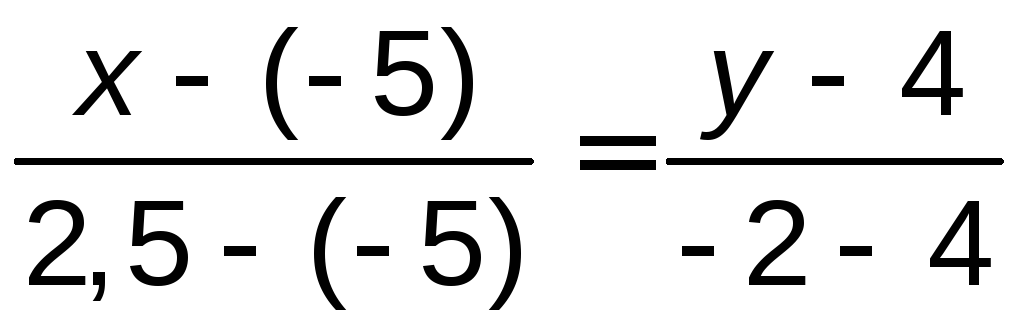 ,
,![]() ,
,![]() .
Разделив обе части уравнения на 1,5,
получим более удобный вид
.
Разделив обе части уравнения на 1,5,
получим более удобный вид![]() − уравнение медианы АМ.
− уравнение медианы АМ.
Пример 2.Напишите уравнение
прямой![]() ,
проходящей через точку М(7;4) параллельно
прямой
,
проходящей через точку М(7;4) параллельно
прямой![]() .
.
Решение.Первый способ.
Согласно формуле (3.5), уравнение любой
прямой, проходящей через точку М, может
быть записано в виде![]() .
Поскольку искомая прямая должна быть
параллельна прямой
.
Поскольку искомая прямая должна быть
параллельна прямой![]() ,
то их угловые коэффициенты совпадают.
Запишем
,
то их угловые коэффициенты совпадают.
Запишем![]() в виде уравнения прямой с угловым
коэффициентом
в виде уравнения прямой с угловым
коэффициентом![]() ,
откуда
,
откуда![]() .
Следовательно, искомая прямая имеет
уравнение
.
Следовательно, искомая прямая имеет
уравнение![]() или
или![]() .
.
Второй способ. Будем искать уравнение
прямой в виде![]() .
Поскольку прямая проходит чрез точку
М(7;4), то координаты этой точки удовлетворяют
уравнению. И можно записать
.
Поскольку прямая проходит чрез точку
М(7;4), то координаты этой точки удовлетворяют
уравнению. И можно записать![]() .
Данная прямая параллельна прямой
.
Данная прямая параллельна прямой![]() ,
для которой
,
для которой![]() ,
,![]() .
Подставив эти значения в предыдущее
уравнение, получим
.
Подставив эти значения в предыдущее
уравнение, получим![]() ,
,![]() .
Окончательно запишем, что уравнение
искомой прямой имеет вид
.
Окончательно запишем, что уравнение
искомой прямой имеет вид![]() .
.
Замечание.Если дано общее
уравнение прямой![]() ,
тоуравнение параллельной прямой,
проходящей через заданную точкух1,у1, имеет
вид
,
тоуравнение параллельной прямой,
проходящей через заданную точкух1,у1, имеет
вид
![]() .
(4.11)
.
(4.11)
Пример 3. Проверить, принадлежит
ли точка М(2;-4) прямой![]() .
.
Решение.Подставим координаты
точки М в левую часть уравнения прямой![]() .
Поскольку левая часть не равна правой:
.
Поскольку левая часть не равна правой:![]() ,
то точка М не принадлежит прямой
,
то точка М не принадлежит прямой![]() .
.
Пример 4. На прямой![]() найти точку, у которой ордината
найти точку, у которой ордината![]() .
.
Решение. Подставив в уравнение
прямой значение![]() найдем абсциссу
найдем абсциссу![]() :
:![]() ;
;![]() .
Искомая точка
.
Искомая точка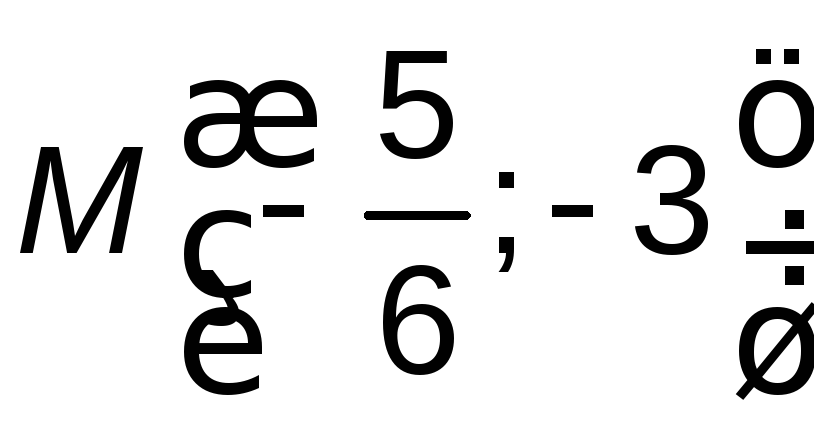 .
.
Пример 5. Найти координаты вершин![]() параллелограмма
параллелограмма![]() ,
если известны координаты вершины
,
если известны координаты вершины![]() ,
а также уравнение сторон
,
а также уравнение сторон![]() :
:![]() и
и![]() :
:![]() .
.
Р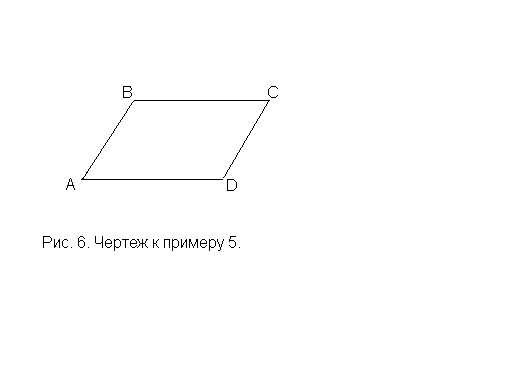 ешение.Решая эту задачу, необязательно (и даже
не нужно) рисовать данные в условии
прямые и точки в декартовых координатах.
Достаточно (для себя) нарисовать
произвольный параллелограмм, чтобы
определиться с расположением вершин и
сторон (рис. 6). Окончательный чертеж
можно выполнить после получения решения.
ешение.Решая эту задачу, необязательно (и даже
не нужно) рисовать данные в условии
прямые и точки в декартовых координатах.
Достаточно (для себя) нарисовать
произвольный параллелограмм, чтобы
определиться с расположением вершин и
сторон (рис. 6). Окончательный чертеж
можно выполнить после получения решения.
Поскольку
![]() ,
то, используя условие параллельности
двух прямых (4.11), можно записать
,
то, используя условие параллельности
двух прямых (4.11), можно записать![]() ,
,![]() − уравнение прямойDC.
ПрямаяAD, заданная
уравнением
− уравнение прямойDC.
ПрямаяAD, заданная
уравнением![]() ,
параллельна оси ОХ
,
параллельна оси ОХ![]() .
И поскольку точка
.
И поскольку точка![]() принадлежит прямойВС, то уравнение
принадлежит прямойВС, то уравнение![]() полностью определяет эту прямую. Теперь,
когда известны уравнения всех сторон
параллелограмма, его вершины найдем из
решения систем вида (4.10). Точка А −
пересечение прямыхАВиAD:
полностью определяет эту прямую. Теперь,
когда известны уравнения всех сторон
параллелограмма, его вершины найдем из
решения систем вида (4.10). Точка А −
пересечение прямыхАВиAD:
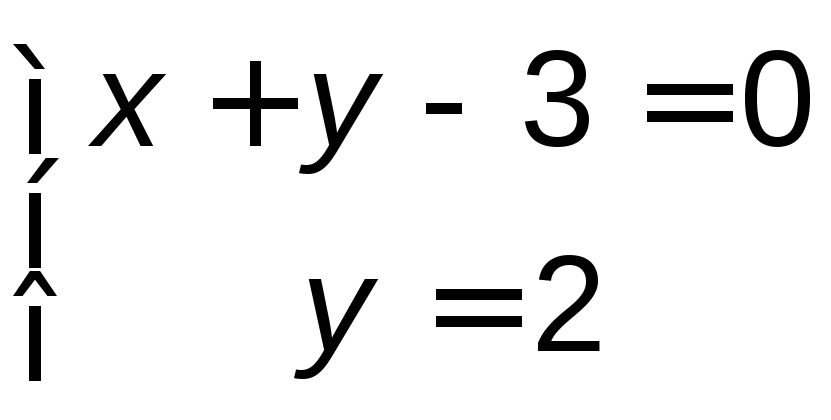
![]()
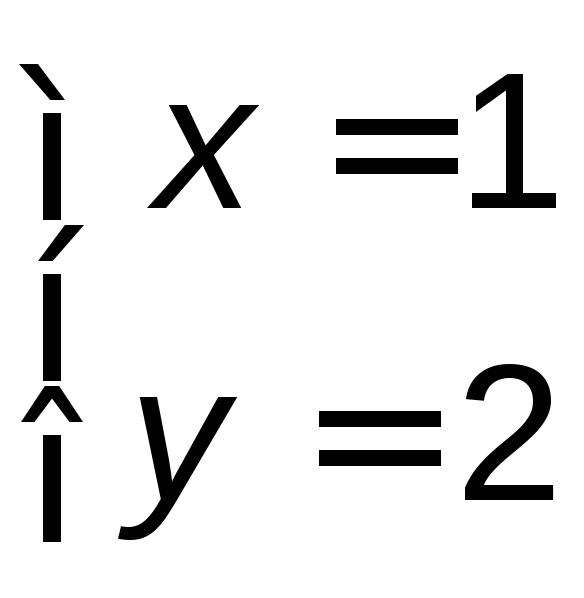
![]()
![]() .
.
Точка В − пересечение прямых АВиВС:
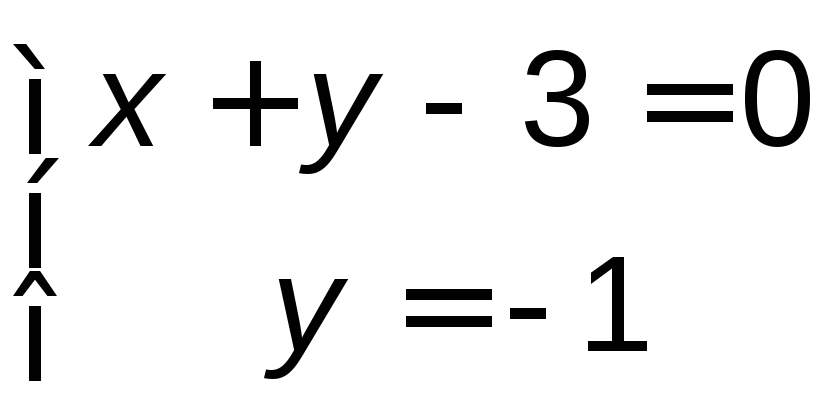
![]()
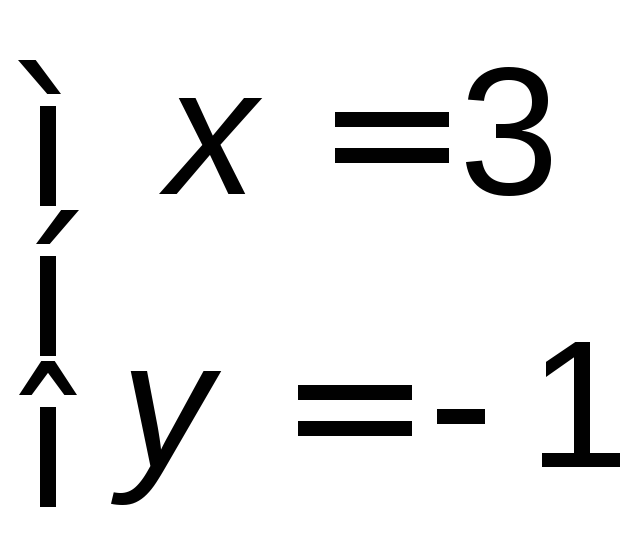
![]()
![]() .
.
Точка
![]() − пересечение прямыхADиDC:
− пересечение прямыхADиDC:
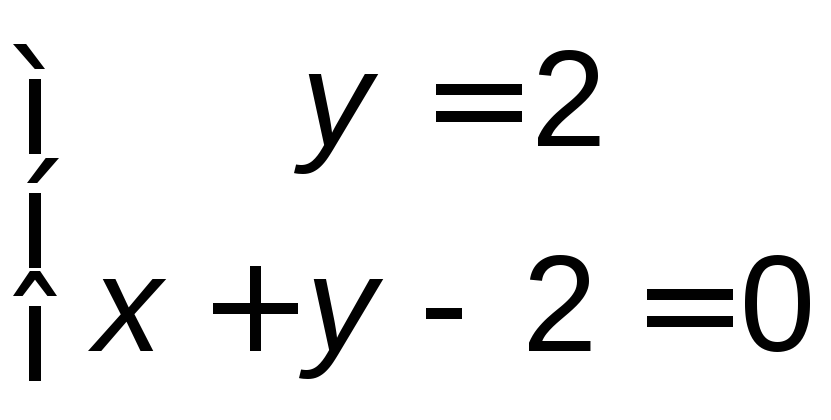
![]()
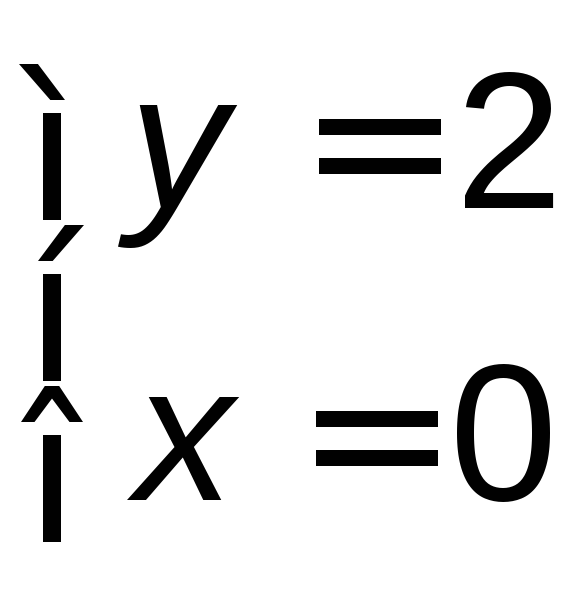
![]()
![]() .
.
Ответ: координаты точек
![]() ,
,![]() ,
,![]() .
.
Пример 6. Найти уравнение прямой![]() ,
проходящей через точку М(1;1), перпендикулярно
прямой
,
проходящей через точку М(1;1), перпендикулярно
прямой![]()
![]() .
.
Решение. Перепишем уравнение![]() в виде
в виде![]() .
Таким образом, угловой коэффициент
данной прямой
.
Таким образом, угловой коэффициент
данной прямой![]() .
Если прямая, проходящая через точку М,
перпендикулярна данной, то их угловые
коэффициенты связаны соотношением
(4.4):
.
Если прямая, проходящая через точку М,
перпендикулярна данной, то их угловые
коэффициенты связаны соотношением
(4.4):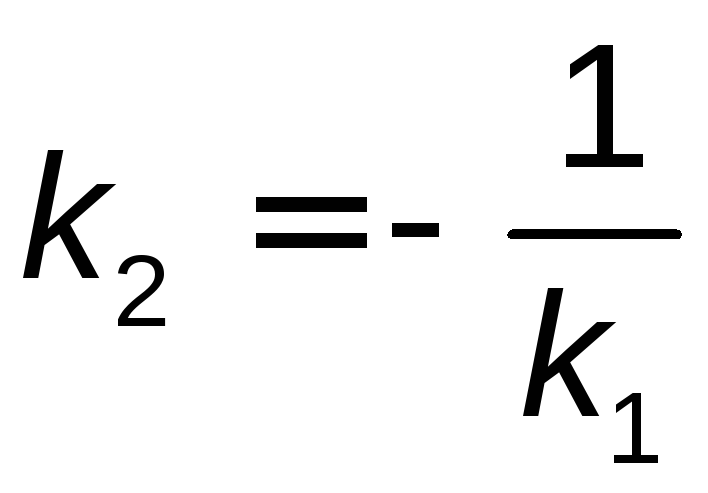 ,
откуда
,
откуда![]() .
В соответствии с формулой (3.5), можно
записать уравнение искомой прямой
.
В соответствии с формулой (3.5), можно
записать уравнение искомой прямой![]() ,
проходящей через точку М(1;1) перпендикулярно
прямой
,
проходящей через точку М(1;1) перпендикулярно
прямой![]()
![]() или
или![]() ;
;![]() .
.
Ответ: уравнение прямой
![]() .
.
Пример 6.1. Найти расстояние от
точки М(1;1) до прямой![]()
![]() .
.
Решение.Расстояниемdот точки до прямой называется длина
перпендикуляра, опущенного из точки М
на прямую. Поэтому сначала запишем
уравнение прямой, проходящей через
точку М перпендикулярно данной прямой.
Эта часть задания нами уже выполнена в
примере 6, поэтому воспользуемся готовым
результатом и запишем, что нужная нам
прямая![]() имеет уравнение
имеет уравнение![]() .
Найдем точку А пересечения прямых
.
Найдем точку А пересечения прямых![]() и
и![]() ,
решая систему
,
решая систему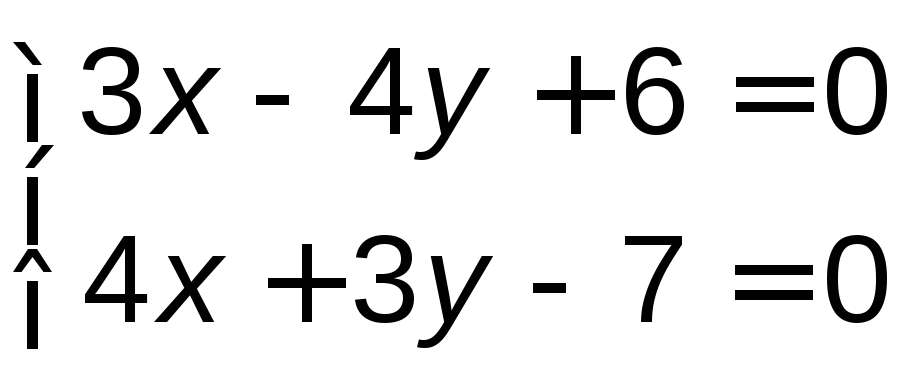 ;
;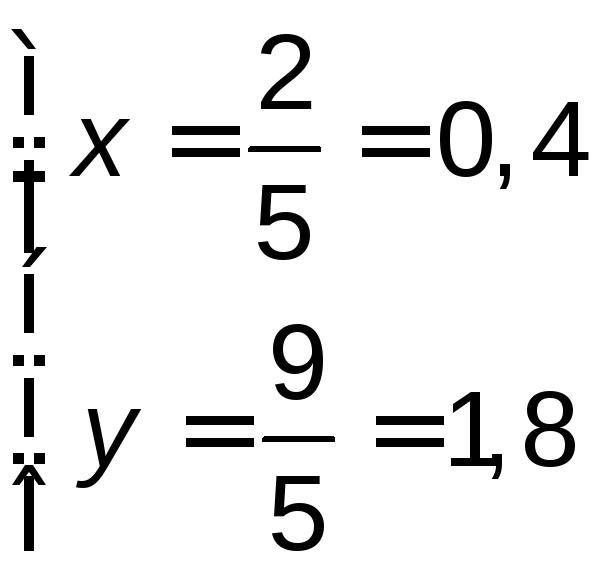 ;
; .
Расстояние между точками А и М вычислим
по формуле (2.1):
.
Расстояние между точками А и М вычислим
по формуле (2.1):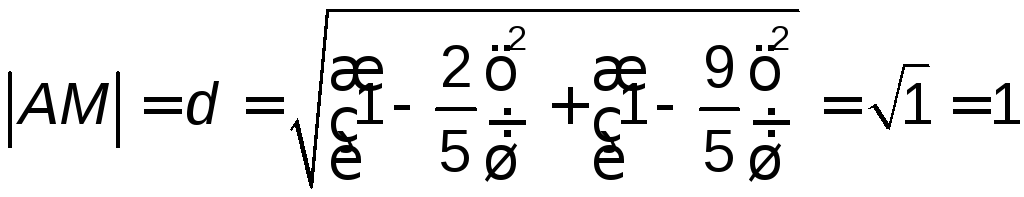 .
.
Ответ: расстояние от точки М до прямой d=1.
Замечание. Можно вывести формулу
расстояния от точки![]() до прямой
до прямой![]() в общем случае, используя рассуждения
примера 6.1. Тогда получим формулу
в общем случае, используя рассуждения
примера 6.1. Тогда получим формулу
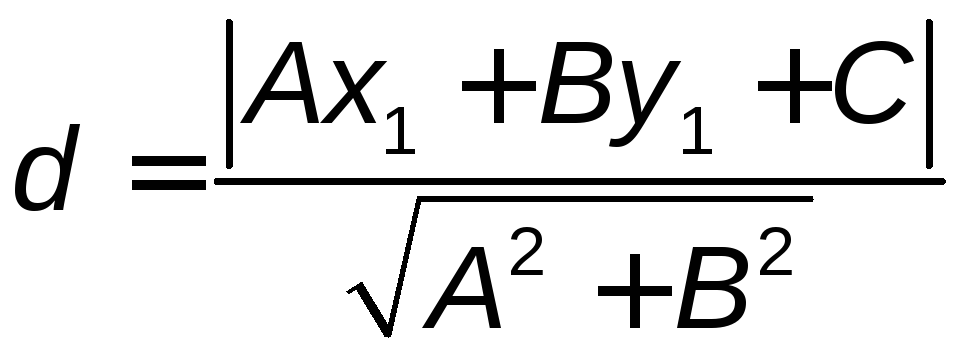 ,
(4.12)
,
(4.12)
определяющую расстояние от точки до прямой. Вместо слов «расстояние от точки до прямой» иногда используют выражение «отклонение точки от прямой».
Пример 7.Через точку![]() провести прямую под углом
провести прямую под углом![]() к прямой
к прямой![]() .
.
Решение. Обозначим прямую![]() как
как![]() ,
а искомую прямую, проходящую через точку
М, как
,
а искомую прямую, проходящую через точку
М, как![]() .
Уравнение прямой, проходящей через
точку М, имеет вид (см. формулу (3.5)):
.
Уравнение прямой, проходящей через
точку М, имеет вид (см. формулу (3.5)):![]() или
или![]() .
Здесь
.
Здесь![]() − угловой коэффициент прямой
− угловой коэффициент прямой![]() .
Записав уравнение прямой
.
Записав уравнение прямой![]() в виде
в виде![]() ,
найдем ее угловой коэффициент
,
найдем ее угловой коэффициент![]() .
Поскольку известен угол
.
Поскольку известен угол![]() между прямыми, то согласно формуле (4.3)
между прямыми, то согласно формуле (4.3) ;
;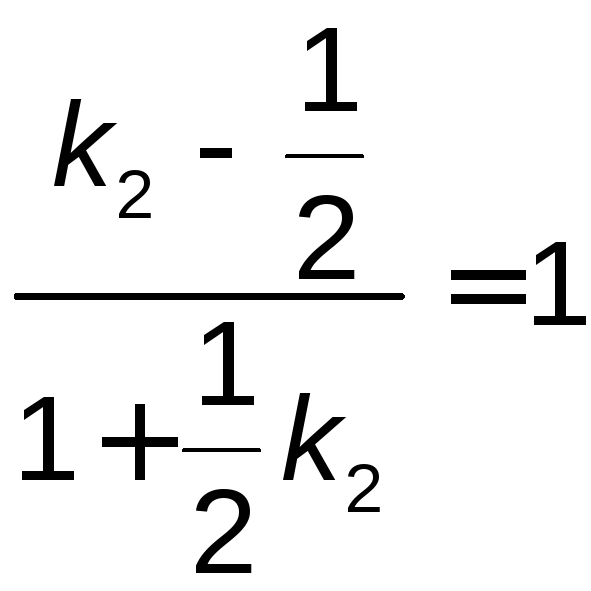 ;
;![]() ;
;![]() .
Теперь окончательно запишем уравнение
искомой прямой
.
Теперь окончательно запишем уравнение
искомой прямой![]() или
или![]() .
.
П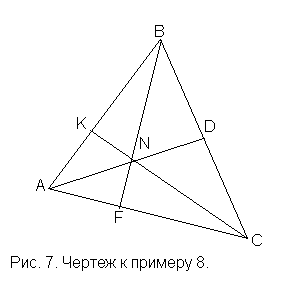 ример
8.Даны две вершины треугольника
ример
8.Даны две вершины треугольника![]() и
и![]() .
Его высоты пересекаются в точке
.
Его высоты пересекаются в точке![]() .
Определить координаты третьей вершины
треугольника
.
Определить координаты третьей вершины
треугольника![]() .
.
Решение.Для удобства рекомендуется нарисовать произвольный треугольник АВС (рис. 7).
Пусть AD,BFиCK– высоты треугольника
АВС,N– точка пересечения
высот. В связи с этимANиADопределяют одну и ту же
прямую. Аналогично для парBNиBF, а такжеCNиCK. Согласно формуле
(3.1) уравнение прямойBN(или, что то же самое, прямойBF:![]() ;
;![]() ;
;![]() ;
;![]() − прямаяBF.Аналогично,
уравнение прямой AN
(или AD):
− прямаяBF.Аналогично,
уравнение прямой AN
(или AD):
![]() ;
;![]() −
прямая AD.
−
прямая AD.
Запишем уравнение стороны ВС как уравнение прямой, проходящей через точку В, перпендикулярно прямой AD. ПосколькуADопределяется уравнением y=const, то перпендикулярная ей прямая ВС будет иметь уравнение x=const. А так как эта прямая проходит через точку В, то абсцисса точки В и определит уравнение ВС: х=6.
Уравнение стороны АС запишем как
уравнение прямой, проходящей через
точку А перпендикулярно прямой BF,
согласно формулам (4.4) и (3.5). Так как
угловой коэффициентBFизвестен:![]() ,
то угловой коэффициент АС – это
,
то угловой коэффициент АС – это![]() ,
поэтому уравнение АС:
,
поэтому уравнение АС:![]() ;
;![]() − уравнение АС.
− уравнение АС.
Точка С теперь может быть найдена как
пересечение прямых ВС
и АС:
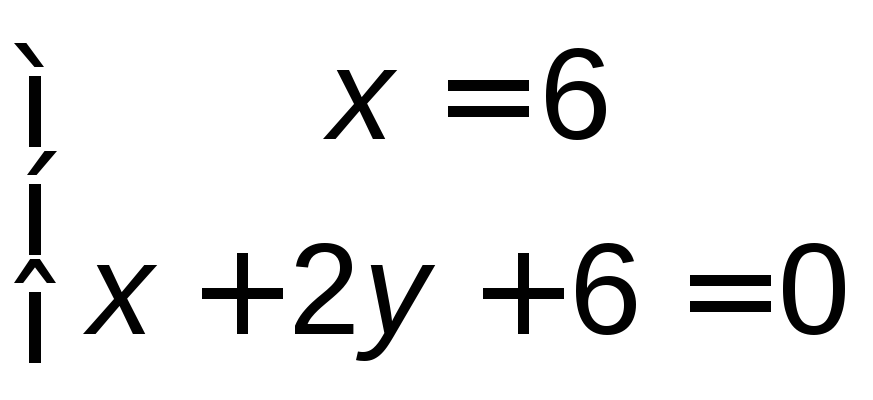 ;
;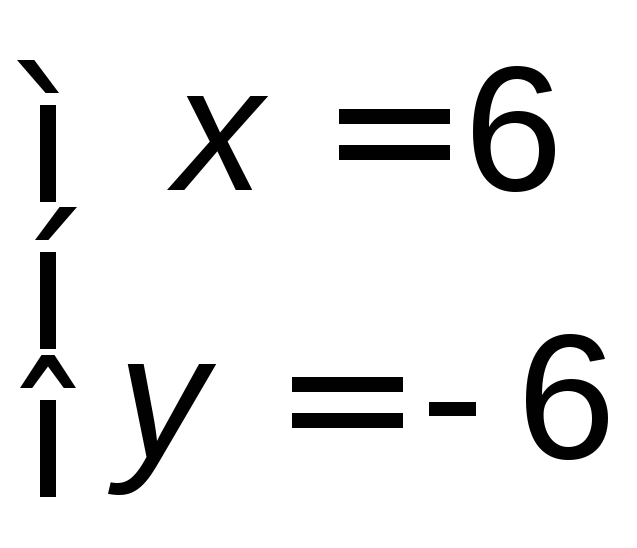 ;
;![]() .
.
Ответ: С(6;-6).
