
- •Введение
- •1. Прямоугольная система координат на плоскости
- •2. Отрезок. Длина отрезка. Деление отрезка в данном отношении
- •3. Уравнение прямой в декартовых координатах
- •4. Взаимное расположение прямых на плоскости
- •5. Задания для самостоятельной работы
- •Заключение
- •Библиографический список
- •Прямая на плоскости
- •680021, Г. Хабаровск, ул. Серышева, 47.
3. Уравнение прямой в декартовых координатах
Положение прямой вполне определено, если заданы какие-либо две ее точки или дана одна точка и указано направление прямой.
Пусть на прямой АВ зафиксированы две
точки
![]() и
и![]() .
.
Выбранная на этой же прямой произвольная
точка
![]() делит отрезок [AB] в некотором
отношении. Тогда справедливо равенство
делит отрезок [AB] в некотором
отношении. Тогда справедливо равенство
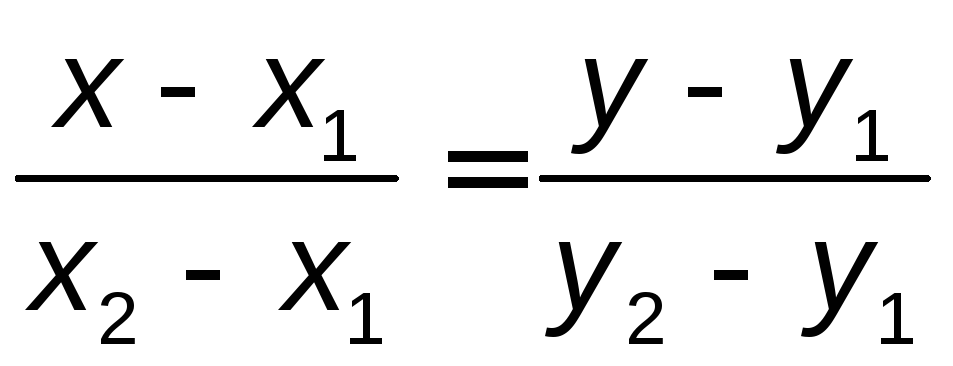 , (3.1)
, (3.1)
которое называется уравнением
прямой, проходящей через две данныеточкиплоскости. Если обозначить![]() ,
,![]() ,
то получим
,
то получим
![]() или
или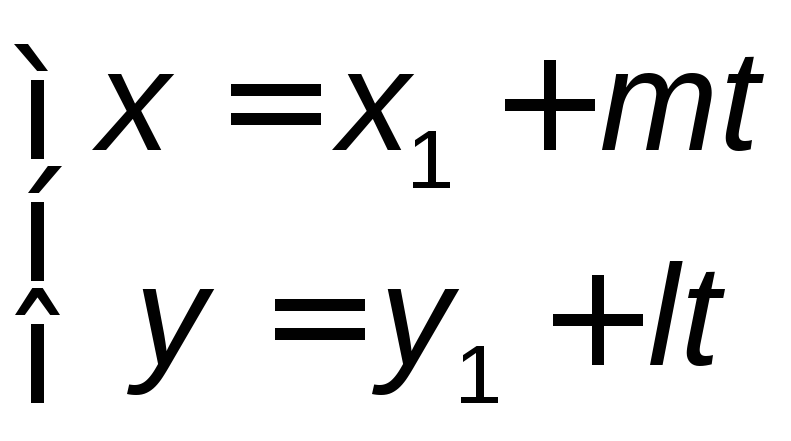 − (3.2)
− (3.2)
параметрическое уравнение прямойна плоскости.
Замечание. Формулы (3.1) и (3.2)
следует понимать как пропорции, в которых
значения![]() и
и![]() могут быть равны нулю.
могут быть равны нулю.
Пример 1. Даны вершины треугольника АВС: А(1;3). В(4;0), С(-4;3). Записать уравнения его сторон.
Решение. Используем формулу (3.1) и запишем:
(АВ):
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(АС):
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(ВС):
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Ответ. (АВ):
![]() ;
(АС):
;
(АС):![]() ;
(ВС):
;
(ВС):![]() .
.
Как видно из предыдущего примера, преобразование выражения (3.1) приводит к уравнению
![]() ,
(3.3)
,
(3.3)
которое называется общим уравнением прямой. Это алгебраическое уравнение первой степени относительно двух переменных, называемое также линейным уравнением.
Таким образом, уравнение всякой прямой можно записать в виде (3.3), где А и В одновременно не равны нулю. Верно и обратное, т.е. уравнение (3.3) всегда определяет прямую.
Зная уравнение прямой, можно её построить, произвольно задавая две какие-либо её точки.
Пример 2.Дано общее уравнение
прямой![]() .
Построить эту прямую.
.
Построить эту прямую.
Решение.Возьмем два произвольных
значения![]() и вычислим соответствующие значения
и вычислим соответствующие значения![]() .
Пусть
.
Пусть![]() ,
тогда
,
тогда![]() ,
,![]() .
Пусть
.
Пусть![]() ,
тогда
,
тогда![]() ,
,![]() .
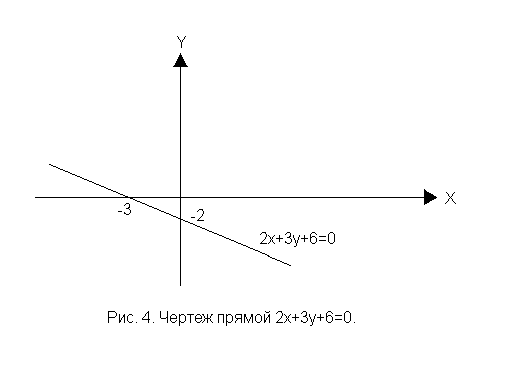
Таким образом, прямая проходит через
точки (0;-2) и (-3;0) (рис. 4).
.
Таким образом, прямая проходит через
точки (0;-2) и (-3;0) (рис. 4).
Рассмотрим частные случаи уравнения (3.3), в которых какие-либо из коэффициентов А, В, С равны нулю:
если прямая проходит через начало координат, то в уравнении (3.3)
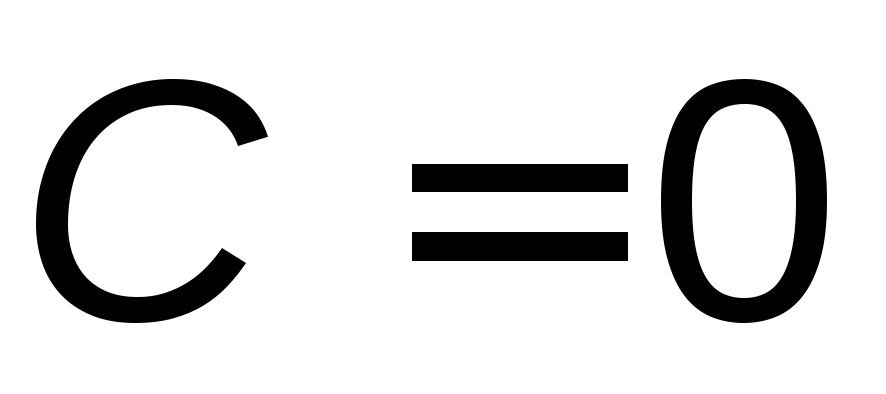 :
: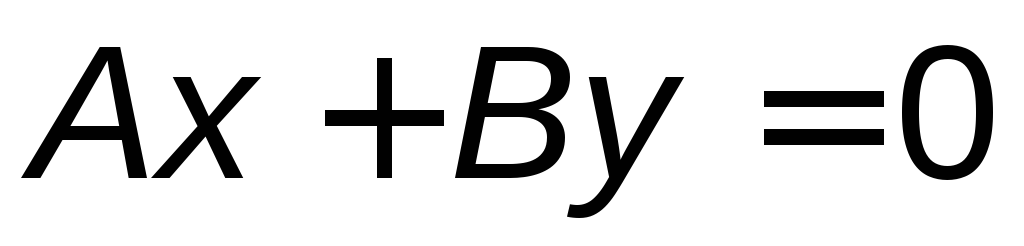 ;
;если прямая параллельна оси абсцисс ОХ, то
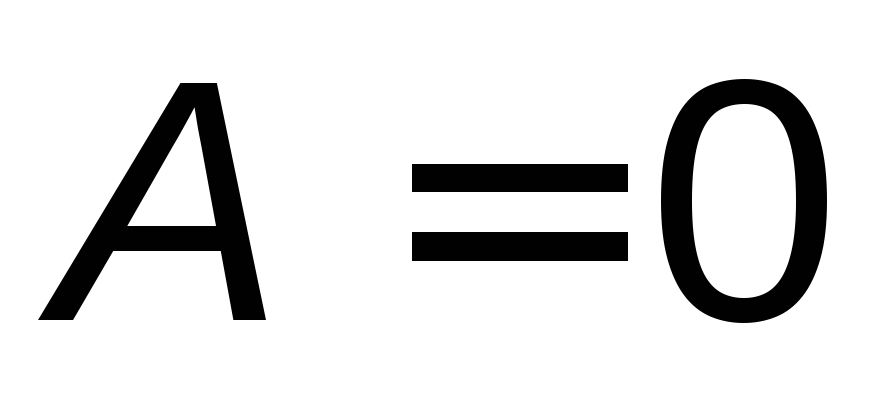 :
: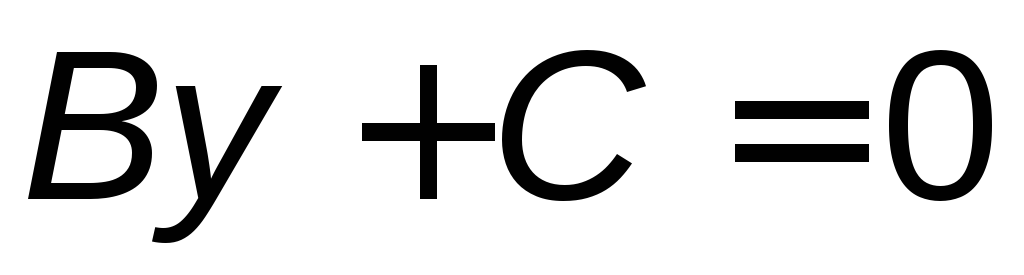 или
или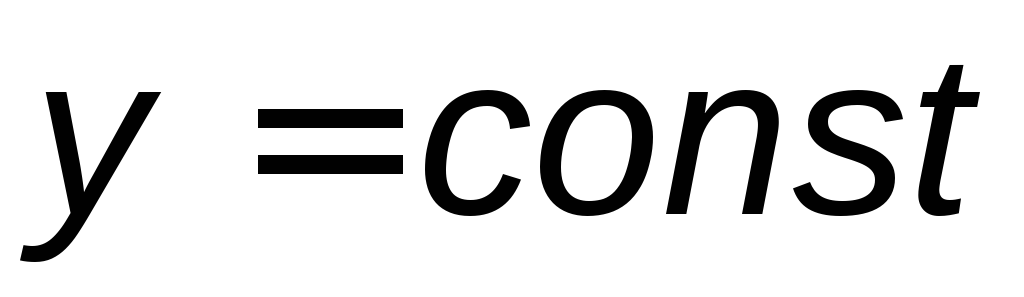 ;
;если прямая параллельна оси ординат ОУ, то
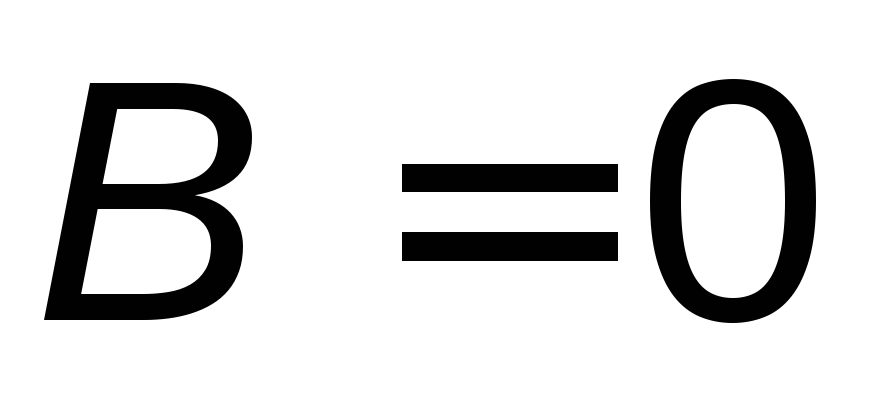 :
: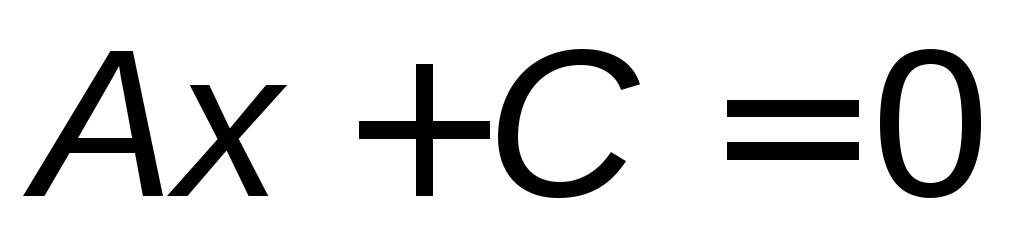 или
или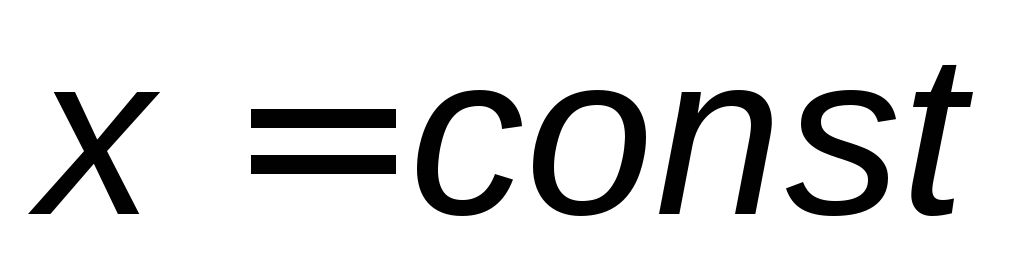 ;
;уравнение
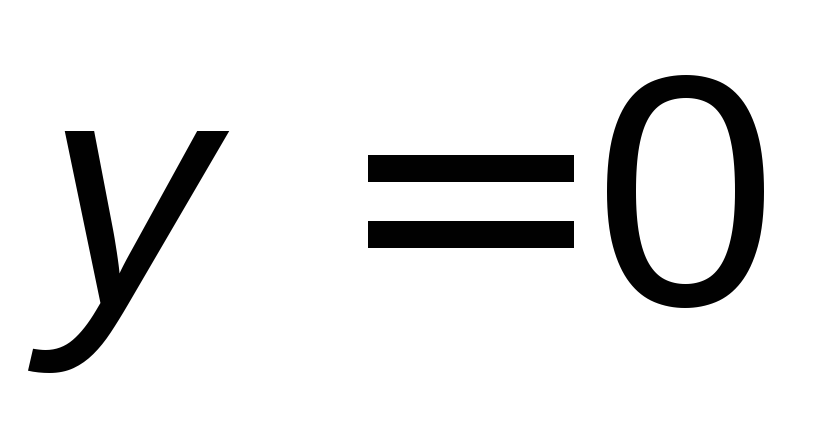 определяет ось ОХ (одновременно
выполняются условия 1) и 2)). Уравнение
определяет ось ОХ (одновременно
выполняются условия 1) и 2)). Уравнение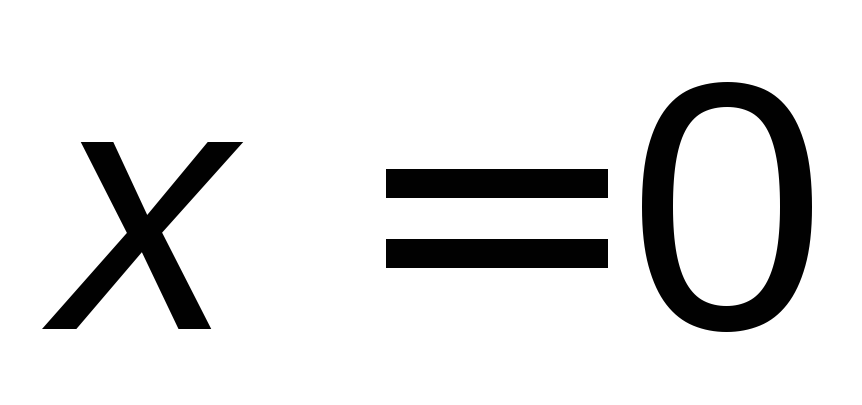 определяет ось ОУ.
определяет ось ОУ.
Пример 3. Уравнение![]() определяет прямую, проходящую через
точку
определяет прямую, проходящую через
точку![]() параллельно оси абсцисс. Уравнение
параллельно оси абсцисс. Уравнение![]() определяет прямую, проходящую через
точку (-2;0), параллельно оси ординат.
Прямая
определяет прямую, проходящую через
точку (-2;0), параллельно оси ординат.
Прямая![]() проходит через начало координат и
представляет собой биссектрису первого
и третьего координатных углов.
проходит через начало координат и
представляет собой биссектрису первого
и третьего координатных углов.
Если в общем уравнении прямой (3.3) коэффициент В не равен нулю, то уравнение (3.3) можно привести к виду
![]() ,
(3.4)
,
(3.4)
которое называется уравнением прямой с угловым коэффициентом.
Действительно, решая относительно
![]() уравнение (3.3), получим
уравнение (3.3), получим![]() .
Обозначая
.
Обозначая![]() ,
,![]() ,
приходим к уравнению (3.4).
,
приходим к уравнению (3.4).
Пример 4.Дано общее уравнение
прямой![]() .
Записать его как уравнение с угловым
коэффициентом.
.
Записать его как уравнение с угловым
коэффициентом.
Решение.Запишем уравнение в
виде![]() ,
откуда
,
откуда![]() ,
,![]() ,
,![]() .
.
Числа
![]() и
и![]() в уравнении (3.4) имеют вполне определенный
геометрический смысл. Угловой коэффициент
в уравнении (3.4) имеют вполне определенный
геометрический смысл. Угловой коэффициент![]() −
это тангенс угла, образованного прямой
с положительным направлением оси ОХ
(отсчет ведется от оси абсцисс в
направлении против часовой стрелки):
−
это тангенс угла, образованного прямой
с положительным направлением оси ОХ
(отсчет ведется от оси абсцисс в
направлении против часовой стрелки):![]() .
Число
.
Число![]() показывает ординату пересечения прямой
с осью ОУ (рис. 5).
показывает ординату пересечения прямой
с осью ОУ (рис. 5).
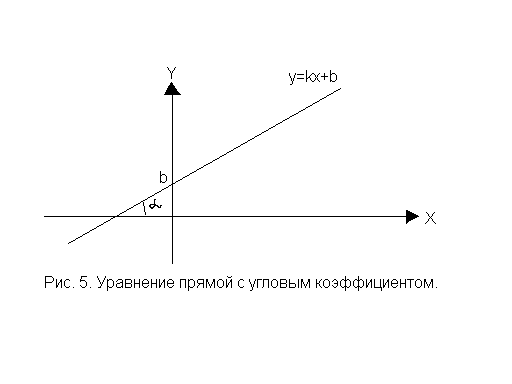
Таким образом, два параметра
![]() и
и![]() полностью определяют положение прямой.
Случай
полностью определяют положение прямой.
Случай![]() соответствует прямой
соответствует прямой![]() ,
проходящей через начало координат.
Случай
,
проходящей через начало координат.
Случай![]() определяет прямую
определяет прямую![]() ,
параллельную оси ОХ и проходящую через
точку
,
параллельную оси ОХ и проходящую через
точку![]() .
.
Если теперь мы вернемся к уравнению
прямой, проходящей через две заданные
точки (3.1), то, записав его в виде
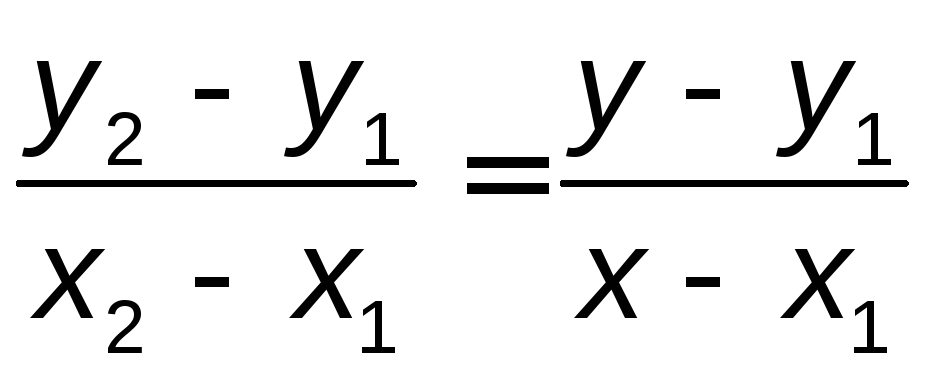 ,
заметим, что отношение
,
заметим, что отношение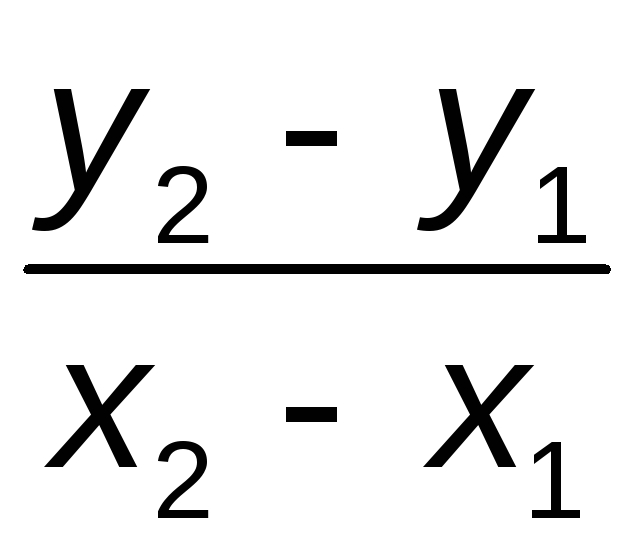 есть не что иное, как тангенс угла наклона
прямой к оси абсцисс, т.е.
есть не что иное, как тангенс угла наклона
прямой к оси абсцисс, т.е.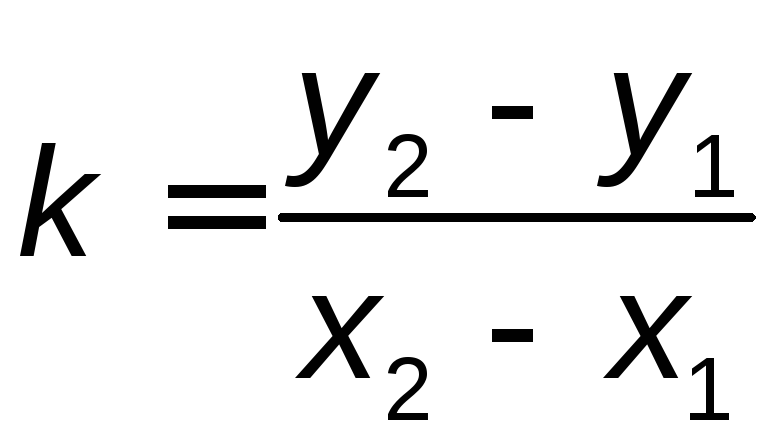 .
Теперь уравнение (3.1) можно переписать
в виде
.
Теперь уравнение (3.1) можно переписать
в виде
![]() .
(3.5)
.
(3.5)
которое является уравнением прямой,
проходящей через заданную точку
![]() .
Задавая различные значения
.
Задавая различные значения![]() ,
мы получим все прямые, проходящие через
точку
,
мы получим все прямые, проходящие через
точку![]() .
Поэтому уравнение (3.5) еще называютуравнением пучка прямыхс центром
в точке
.
Поэтому уравнение (3.5) еще называютуравнением пучка прямыхс центром
в точке![]() .
.
Пример 5. Уравнение![]() определяет любую прямую, проходящую
через точку (2;1). Выбирая различные
значения
определяет любую прямую, проходящую
через точку (2;1). Выбирая различные
значения![]() ,
получим частные случаи прямых, проходящих
через данную точку. Так, если
,
получим частные случаи прямых, проходящих
через данную точку. Так, если![]() ,
то уравнение
,
то уравнение![]() определяет прямую, параллельную оси
абсцисс. Если
определяет прямую, параллельную оси
абсцисс. Если![]() ,
получим
,
получим![]() или
или![]() ,
и т.д.
,
и т.д.
Если в общем уравнении прямой (3.3) все
коэффициенты А, В, С отличны от нуля, то
удобно преобразовать уравнение
![]() к виду
к виду
![]() ,
(3.6)
,
(3.6)
которое называется уравнением прямой
в отрезках. Числа![]() и
и![]() представляют собой координаты пересечения
прямой с осями ОХ и ОУ соответственно.
Переход от уравнения (3.3) к уравнению
(3.6) выполняется так. Записав уравнение
представляют собой координаты пересечения
прямой с осями ОХ и ОУ соответственно.
Переход от уравнения (3.3) к уравнению
(3.6) выполняется так. Записав уравнение![]() в
виде
в
виде![]() ,
делим обе части полученного уравнения
на
,
делим обе части полученного уравнения
на![]() :
:![]() или
или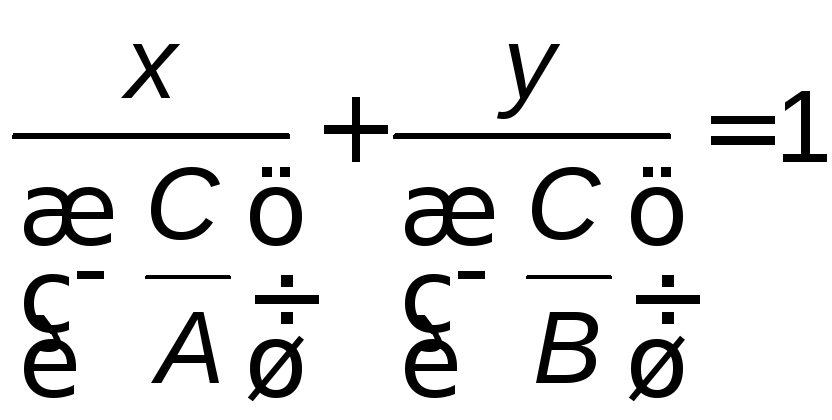 .
Обозначив,
.
Обозначив,![]() ,
,![]() ,
получим (3.6).
,
получим (3.6).
Пример 6.Привести уравнение
прямой![]() к уравнению в отрезках.
к уравнению в отрезках.
Решение. Записав![]() ,
делим обе части равенства на (-6), получаем
,
делим обе части равенства на (-6), получаем![]() или
или![]() .
Прямая пересекает ось ОХ в точке
(-3;0),
а ось ОУ − в точке (0;-2) (см. рис. 4).
.
Прямая пересекает ось ОХ в точке
(-3;0),
а ось ОУ − в точке (0;-2) (см. рис. 4).
