
Физика(II семестр) -Лекция1
.pdf
|
|
|
|
|
|
11 |
p 2mv |
|
1 |
mv2 n . |
(10.28) |
||
|
||||||
i |
i i |
|
3 |
i i |
|
|
|
|
|
|
|
||
Полное давление получим, просуммировав (10.28) по всем группам ni молекул:
p pi 13 m vi2 ni .
Разделив и умножив последнюю сумму в этом выражении на n , получим
|
|
|
p |
1 |
nm v2 . |
|
(10.29) |
|||
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
|||
Это выражение можно переписать иначе: |
|
|||||||||
|
|
|
p |
2 |
n |
|
, |
(10.30) |
||
|
|
|
|
пост |
||||||
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
||||
где |
пост |
mv2 |
/ 2 – среднее значение |
поступательной |
кинетической |
|||||
|
|
|
|
|
|
|
|
|
|
|
энергии молекул.
Эту формулу называют основным уравнением кинетической теории газов. Она раскрывает физический смысл макропараметра р: давление газа на стенку определяется средним значением поступательной кинетической энергии молекул (и только поступательной!).
Отметим, что это выражение является точным, несмотря на то, что расчет имеет довольно грубый оценочный характер. Дело в том, что в процессе расчета были допущены две неточности в числовых коэффициентах, которые случайным образом (так иногда бывает) компенсировали друг друга. А именно, для числа столкновений и передаваемом стенке в среднем импульсе p каждой молекулой мы использовали коэффициенты со-
ответственно 1/6 и 2. Точный же расчет дает 1/4 и 4/3. Как видим, их произведение в обоих случаях равно 1/3.
Физический смысл температуры T . Сопоставив полученное выражение (10.30) с уравнением Клапейрона (10.7), находим
|
|
|
|
|
|
|
3 |
kT . |
(10.31) |
|
пост |
|
|||||||||
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
где k – постоянная Больцмана |
|
|
|
|
|
|
|
|||
|
k R / N |
A |
1.3810 23 Дж/К . |
(10.32) |
||||||
|
|
|
|
|
|
|
|
|
|
|
Формула (10.31) замечательна тем, что вскрывает физический смысл |
||||||||||
температуры Т: температура T выражает среднюю |
кинетическую |
|||||||||
энергию молекул. |
|
|
|
|
|
|
|
|
|
|
Следует обратить внимание, что |
|
пост зависит только от Т, от массы |
||||||||
же молекул не зависит. |
|
|
|
|
|
|
|
|||
Заменив в (10.30) пост его выражением (10.31), получим |
||||||||||
|
|
|
|
p nkT , |
(10.33) |
|||||
где n – концентрация молекул.
Это несколько иная форма уравнения состояния идеального газа. Формулу
12
(10.33) можно, конечно, получить и сразу из уравнения pVM RT , разделив обе части на VM и представив R как kNA
Гипотеза о равнораспределении энергии по степеням свободы Степени свободы. Так называют число независимых координат, оп-
ределяющих положение системы, или в интересующем нас случае – молекулы. Для определения положения центра масс молекулы необходимо задать три координаты. Это означает, что молекула имеет три поступательных степени свободы.
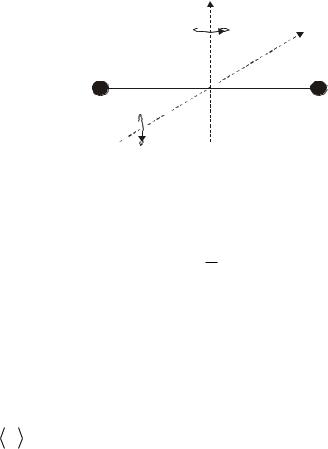
Если молекула двухатомная и жесткая («гантель»), то, кроме трех поступательных степеней свободы, она имеет и две вращательные, связанные с углами поворота вокруг двух взаимно перпендикулярных осей 1-1 и
2-2, проходящих через центр масс С, как |
|
|
|
показано на рис.10.9. Вращение вокруг оси |
|
2 |
|
молекулы для материальных точек лишено |
|
|
|
смысла. |
|
1 |
|
Таким образом, жесткая двухатомная |
|
|
|
молекула имеет пять степеней свободы: три |
|
|
|
поступательных и две вращательных. |
|
2 |
|
Если молекула упругая, то возможны |
1 |
||
|
колебания атомов и необходима еще одна
степень свободы (расстояние между атома- |
Рис.10.9 |
|
ми). Ее называют колебательной.
Гипотеза о равнораспределении. Тот факт, что средняя энергия по-
ступательного движения молекулы согласно (1.31) равна 32 kT , означает,
что на каждую степень свободы в среднем приходится энергия kT / 2 . Больцман обобщил этот вывод в виде гипотезы, о равном, распределении средней энергии по степеням свободы. При этом на колебательную степень свободы должны приходиться в среднем по две половинки kT – одна в виде кинетической и одна в виде потенциальной (как мы знаем, их средние значения одинаковы). Итак, средняя энергия молекулы
|
i |
kT , |
(10.34) |
|
|||
2 |
|
|
|
где i – сумма числа поступательных zпост , вращательных zвр |
и удвоен- |
||
ного числа колебательных zкол степеней свободы: |
|
||
i zпост zвр zкол . |
(10.35) |
||
Число i совпадает с числом степеней свободы только для жестких молекул.
Приведем некоторые важные результаты для числа степеней свободы у линейных и нелинейных молекул, учитывая, что полное число степеней свободы у системы из N материальных точек равно ЗN. Эти результаты приведены в табл. 10.1.

Пример. Выясним, какие колебательные степени свободы возможны у линейной молекулы CO2
Согласно приведенной таблице таких колебаний должно быть четыре(3·3–5=4). Эти колебания (в Ц– системе) показаны на рис 10.10, и их действительно четыре, поскольку в случае а) возможны колебания как в плоскости рис, так и в перпендикулярной к ней (две поляризации).
13
Рис.10.10
|
|
|
|
|
|
Таблица 10.1 |
|
Молекула |
жесткая |
|
упругая |
||||
|
|
|
i=zпост+zвр |
|
i=zпост+zвр+2zкол |
||
Линейная |
z 3пост |
2вр |
5 |
zкол 3N 5 |
|||
|
|
|
z 3 |
3 |
6 |
zкол 3N 6 |
|
Нелинейная |
|||||||
пост |
вр |
|
|
||||
|
|
|
|
|
|
|
|
Внутренняя энергия. Эту энергию для моля идеального газа можно найти, умножив (10.34) на постоянную Авогадро:
U |
i |
RT , |
(10.36) |
M |
2 |
|
где R kNA .
Учитывая (10.11) и (10.14), получим выражения для молярных теплоемкостей:
CV iR / 2, |
Cp (i 2)R / 2 . |
(10.37) |
||
и их отношение – постоянную адиабаты , равную Cp / CV : |
|
|||
|
i 2 |
. |
(10.38) |
|
|
||||
|
|
i |
|
|
Согласно этой формуле для молекулы одноатомной 1.67 , жесткой двухатомной 1.40 и упругой двухатомной 1.29 . Эти значения
хорошо согласуются с опытными данными в области комнатных температур.
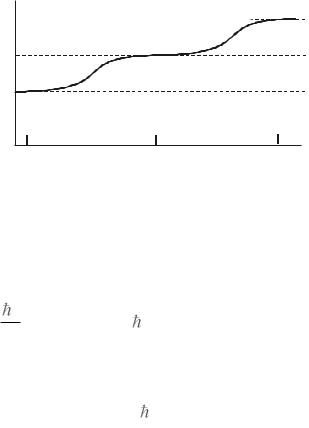
Отсюда, казалось бы, следует, что гипотеза о равнораспределении энергии по степеням свободы подтверждается, однако расширение температурного интервала исследований показало иное (рис.10.11). Вообще говоря, изначально данная гипотеза была не очень понятна: почему, например, двухатомная молекула (как и атом) не может вращаться вокруг своей оси, или почему «жесткая» молекула не испытывает колебаний.
Парадоксально, но успех гипотезы о равнораспределении энергии по степеням свободы связан с отказом от этой гипотезы. Успех был основан
|
|
|
|
|
|
14 |
на том, что некоторые сте- |
|
C /R |
|
|
|
|
7/2 |
V |
|
|
|
||
пени свободы искусственно |
|
|
|
3 |
||
исключались без каких-либо |
5/2 |
|
|
2 |
|
|
убедительных обоснований. |
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
||
А если заглянуть вглубь мо- |
3/2 |
1 |
|
|
|
|
лекулы или атома, то сразу |
|
|
|
|
||
|
|
|
|
|
||
обнаруживается, что множе- |
0 |
|
|
|
|
|
ство степеней свободы про- |
50 100 |
|
500 |
1000 T, K |
||
|
|
|||||
сто проигнорировано?! |
|
|
|
|
|
|
|
Все эти вопросы были |
|
|
|
Рис.10.11 |
|
|
|
|
|
|
|
|
полностью разрешены толь- |
|
|
|
|
|
|
ко в рамках квантовой теории. Известно, что вращательная и колебатель- |
||||||
ная энергии квантованы. Их уровни определяются соответственно форму- |
||||||
лами |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Er |
|
r(r 1), |
En |
(n 1/ 2) , |
(10.39) |
|
|
2I |
|
r 0,1,2,... , n – колебательное |
||
где |
r – вращательное квантовое число |
|||||
n 0,1,2,... , I – момент инерции молекулы относительно той или иной |
||||||
главной оси, – собственная частота колебаний, |
– постоянная Планка. |
|||||
|
Из этих формул следует, что минимальная вращательная энергия |
|||||
молекулы H2 равна порядка одной сотой эВ. И при такой низкой темпера- |
||||||
туре как 50 К (участок 1 на рис. 10.11) средняя энергия поступательного |
||||||
движения молекулы вдвое меньше минимальной вращательной энергии. |
||||||
Т.е. ее оказывается недостаточно, чтобы возбудить вращательные степени |
||||||
свободы. В этих условиях, как говорят, вращательные степени свободы |
||||||
«заморожены». |
|
|
|
|
|
|
|
В области температур ~500 К, соответствующих участку 2, враща- |
|||||
тельные степени свободы полностью разморожены, и молекула H2 ведет |
||||||
себя как жесткая двухатомная молекула с числом степеней свободы 3+2=5. Заметим, что включаются две, а не три вращательные степени свободы. Это связано с тем, что для включения степени свободы, соответствующей вращению молекулы вокруг ее оси, проходящей через оба ядра, требуется значительно большая энергия из-за малости момента инерции молекулы относительно этой оси, согласно первой из формул (10.39).
При температурах, превышающих 1000 К, энергии уже оказывается достаточно для постепенного возбуждения колебательной степени свободы (полностью – нет, поскольку раньше наступает диссоциация молекулы на два атома, участок 3).
Объяснение зависимости CV (T ) , показанной на рис. 10.11, – это серьезный успех квантовой теории.
Газ Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса. До сих пор мы не выходили за рамки модели идеального газа pVM RT . Однако опыт вы-
15
нуждает уточнить эту модель, поскольку с ростом давления (при T const ) оказывается, что pVM RT . При p 1000 атм pVM становится вдвое
больше, чем предписывает модель идеального газа (газ не «сжимается»). Причин этому две:
1)собственный размер молекул; он и уменьшает объем, доступный для движения молекул, при нормальных условиях он составляет ~0,07 % объема сосуда с газом, а при 100 атм. уже 70%!
2)сложный характер взаимодействия между молекулами.
|
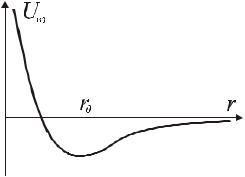
Типичная кривая зависимости энергии взаимодействия |
от расстоя- |
||||
ния |
r между их центрами приведена на |
|
||||
рис.10.12. На малых расстояниях |
r r0 |
|
||||
молекулы отталкиваются, на |
больших |
|
||||
r r0 |
притягиваются. |
|
|
|
|
|
|
Эти причины можно учесть путем |
|
||||
введения поправок в уравнение состояния |
|
|||||
идеальных газов, что и сделал Ван-дер- |
|
|||||
Ваальс. В результате уравнение состояния |
|
|||||
одного моля реального газа приняло вид |
|
|
||||
Рис.10.12 |
||||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a |
|
|
||
|
p |
VM b RT . |
(10.40) |
|||
|
2 |
|||||
|
|
VM |
|
|
||
|
Это и есть уравнение Ван-дер-Ваалъса. Здесь а и b – |
постоянные |
||||
Ван-дер-Ваальса для разных газов они имеют свои значения. |
|
|||||
|
Если мы имеем дело не с одним, а с молями газа объемом V, то в |
|||||
уравнении (10.40) следует сделать замену: VM V / . |
|
|||||
Поправка в первой скобке, a /VM2 , обусловлена силами притяжения
между молекулами. Она имеет размерность давления, и ее часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление р. Однако, если бы силы притяжения между молекулами мгновенно исчезли,
то давление на стенку стало бы p a /VM2 . Т.е. при переходе от идеального
газа к реальному давление на стенку уменьшается – из-за сил притяжения между молекулами.
Поправка b , как легко сообразить, связана с собственным объемом молекул, ее размерность м3/моль.
Газ, подчиняющийся уравнению (1.40), называют ван-дер- ваальсовским. Обращаем на это внимание в связи с тем, что к настоящему времени предложено много других уравнений состояния (свыше 100), более точных, но и более громоздких.
Для наших целей уравнение Ван-дер-Ваальса является предпочтительным: при большой простоте оно дает возможность объяснить, хотя бы качественно, широкий круг явлений в газах и даже в жидкостях.

16
Энергия ван-дер-ваальсовского газа. Внутренняя энергия такого газа U K Uвз , где K – суммарная кинетическая энергия молекул в Ц-системе (связанной с сосудом), Uвз – суммарная энергия взаимодействий молекул (собственная потенциальная энергия). Сначала найдем Uвз . Для этого воспользуемся тем, что работа сил притяжения равна убыли энергии Uвз : dA dUвз . Силы притяжения характеризуются внутренним давлением
p a /V 2 |
в |
уравнении (1.40). |
Тогда |
элементарная работа этих сил |
||||||
i |
M |
|
|
|
|
|
|
|
|
|
A pidVM , |
где знак минус обусловлен тем, |
что при расширении газа |
||||||||
dVM 0 работа A должна быть отрицательной, т.е. A<0. Итак, |
||||||||||
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
A |
|
dV d |
. |
||||
|
|
|
|
|
|
|||||
|
|
|
VM2 |
M |
|
VM |
||||
|
Мы представили A как убыль некоторой величины – она и является |
|||||||||
энергией Uвз : |
|
|
|
|
|
|
|
|
||
|
|
|
Uвз |
a /VM |
(10.41) |
|||||
Константа, которую здесь следовало бы добавить, несущественна. Поэтому мы сразу же положили ее равной нулю. Получается естественный результат: при VM Uвз 0 .
Суммарная же кинетическая энергия K зависит от поступательного
и внутреннего движений молекул, и определяется как |
CV T . |
||||||
Таким образом, внутренняя энергия моля ван-дер-ваальсовского газа |
|||||||
U |
|
C T |
a |
, |
|
(10.42) |
|
M |
|
||||||
|
V |
VM |
|
|
|
|
|
|
|
|
|
|
|
|
|
где CV (i / 2)R . |
|
|
|
|
|
|
|
Если газ расширяется в пустоту без |
|
|
|
|
|||
теплообмена с окружающими |
телами, то |
|
|
|
|
||
|
|
|
|
||||
А=0, Q=0, и согласно первому началу в этом |
|
|
|
процессе U const . Значит, как видно из |
~ |
|
|
(10.42), с ростом объема температура газа |
K=CVT |
V |
|
|
|
||
уменьшается (в отличие от идеального газа). |
|
|
|
Это можно представить и наглядно |
U |
|
|
(рис. 10.13). Видно, что при расширении га- |
|
||
|
|
||
за (увеличении объема V) в случае |
U const |
Рис.10.13 |
|
|
|
|
|
суммарная кинетическая энергия |
молекул |
|
|
газа, а значит и температура Т, уменьшается. Газ охлаждается.
