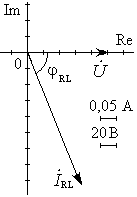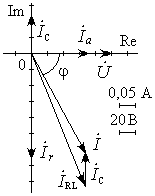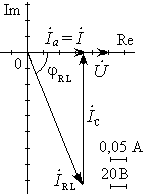- •Новочеркасский ордена Трудового Красного Знамени политехнический институт имени Серго Орджоникидзе
- •Тема 1. Основные понятия и законы теории цепей. Электрические и магнитные цепи.
- •1. Основные термины теории электрических цепей
- •2. Первый закон Кирхгофа
- •3. Второй закон Кирхгофа.
- •4. Основные элементы линейных электрических цепей.
- •5. Эквивалентные преобразования фрагментов электрических цепей.
- •6. Мощность двухполюсника
- •7. Полная система расчетных уравнений эл. Цепи.
- •8. Метод узловых потенциалов
- •9. Магнитные цепи.
- •10. Основные характеристики переменных токов и напряжений.
- •Тема 2. Синусоидальные режимы электрических цепей
- •11. Комплексный метод расчета синусоидальных режимов эл. Цепей.
- •12. Резистор, катушка индуктивности и конденсатор в синусоидальном режиме.
- •13. Комплексное сопротивление и комплексная проводимость.
- •14. Мощность двухполюсника в синусоидальном режиме
- •15. Последовательное соединение резистора, катушки индуктивности и конденсатора.
- •16. Смешанное соединение резистора, катушки индуктивности и конденсатора.
- •17. Трехфазный источник напряжения. Общая характеристика трехфазных цепей.
- •18. Соединение трехфазного источника напряжения и нагрузки звездой
- •19. Соединение трехфазного источника напряжения и нагрузки треугольником
- •Тема 3. Дополнительные главы
- •20. Переходные процессы
- •21. Взаимная индуктивность.
16. Смешанное соединение резистора, катушки индуктивности и конденсатора.
|
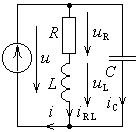
Рис. 16.1. |
Будем понимать эту цепь как модель энергетической системы, состоящей из источника напряжения е, соединенного линией электропередач с нагрузкой в виде последовательно соединенных резистораRи катушки индуктивностиL. Такая модель выбрана, потому что в энергетике большую долю нагрузки составляют электродвигатели и трансформаторы, которые необратимо отбирают электрическую энергию из сети (так, как это делает резистор), а также периодически запасают энергию в магнитном поле своих индуктивностей и отдают ее обратно в цепь (так, как это делает катушка индуктивности).
Емкость С рассчитаем так, чтобы токIв линии электропередач был минимальным. Это позволит свести к минимуму потери энергии в проводах линии электропередач, соединяющей источник энергии и нагрузку (см. п.14, а также лабораторную работу №3 по общей электротехнике). Такой режим часто называют компенсацией реактивной мощности нагрузки.
Согласно определению полной проводимости двухполюсника (см. п.13),
![]() ,
,
то есть, при заданном напряжении Uминимум токаIдостигается при минимуме полной проводимостиy. Найдем эту проводимость, используя эквивалентные преобразования сопротивлений.
Комплексное сопротивление последовательно включенных резистора и катушки будет равно сумме комплексных сопротивлений этих элементов (см. п. 13):
![]() .
.
Комплексная проводимость ветви с резистором и катушкой будет обратна к комплексному сопротивлению этой ветви:
![]() .
.
При параллельном соединении проводимости складываются, поэтому
![]() .
.
Чтобы найти у, удобно выделить действительную и мнимую частьY. Сделаем это, умножив числитель и знаменатель дроби на выражение, комплексно сопряженное знаменателю:
![]() .
.
Используем принятые в электротехнике
обозначения:
![]() – активная проводимость двухполюсника,
– активная проводимость двухполюсника,![]() – реактивная проводимость двухполюсника
(см. п.13).
– реактивная проводимость двухполюсника
(см. п.13).
Согласно определению полной проводимости
![]() (см. п.13).
(см. п.13).
Так как gне зависит
от емкости конденсатораС, тоукак функция отСдостигает минимума
при![]() .
Отсюда получаем формулу для емкости
конденсатора:
.
Отсюда получаем формулу для емкости
конденсатора:
![]() .
.
Обратим внимание на то, что
![]() – это условие фазового резонанса (см.
п.15). Так как при этом сопротивление
двухполюсника максимально, то это в
данном случае фазовый резонанс совпадает
с резонансом токов.
– это условие фазового резонанса (см.
п.15). Так как при этом сопротивление
двухполюсника максимально, то это в
данном случае фазовый резонанс совпадает
с резонансом токов.
Построим векторную диаграмму напряжений
и токов. Вначале нарисуем комплекс
напряжения
![]() (рис. 16.2). Его фазу будем считать нулевой,
поэтому вектор
(рис. 16.2). Его фазу будем считать нулевой,
поэтому вектор![]() направим вдоль действительной оси.
Затем найдем сдвиг фаз между напряжением
и током ветвиRL(см.
пример п. 13):
направим вдоль действительной оси.
Затем найдем сдвиг фаз между напряжением
и током ветвиRL(см.
пример п. 13):![]() - это угол между действительной осью и
вектором, изображающим комплекс тока
ветвиRL.
- это угол между действительной осью и
вектором, изображающим комплекс тока
ветвиRL.
Найдем действующее значение тока ветви
RL:![]() - это длина вектора, изображающего
комплекс тока ветвиRL(в некотором графическом масштабе).
- это длина вектора, изображающего
комплекс тока ветвиRL(в некотором графическом масштабе).
Нарисуем на диаграмме комплекс тока ветви RL (рис. 16.2).
Ток всего двухполюсника
![]() равен сумме тока ветвиRL
равен сумме тока ветвиRL![]() и тока конденсатора
и тока конденсатора![]() :
:![]() .
Ток конденсатора сдвинут по фазе
относительно напряжения на
.
Ток конденсатора сдвинут по фазе
относительно напряжения на![]() .
Нарисуем комплекс тока конденсатора и
сложим его с комплексом тока ветвиRL,
получим ток
.
Нарисуем комплекс тока конденсатора и
сложим его с комплексом тока ветвиRL,
получим ток![]() (рис. 16.3).
(рис. 16.3).
|
Рис. 16.2. Напряжение и ток ветви RL(нагрузки). |
Рис. 16.3. Векторная диаграмма напряжения и тока смешанного соединения RLC (частичная компенсация реактивного тока нагрузки). |
Рис. 16.4. Полная компенсация реактивного тока (резонанс токов). |
На рис. 16.3 видно, что наличие в цепи тока
конденсатора
![]() приводит к уменьшению тока в линии
электропередач
приводит к уменьшению тока в линии
электропередач![]() по сравнению с током нагрузки
по сравнению с током нагрузки![]() .
На рис. 16.4 показан случай, когда ток
.
На рис. 16.4 показан случай, когда ток![]() подобран так, что он обеспечивает минимум
тока
подобран так, что он обеспечивает минимум
тока![]() .
.