- •Государственный комитет рф по связи и
- •Введение
- •Абсолютная и относительная погрешность Определения
- •Изменения абсолютной и относительной погрешностей при арифметических операциях
- •Решение систем линейных уравнений Точные и приближенные методы решения
- •Метод Гаусса – точный метод решения слу
- •Метод простой итерации – приближенный метод решения слу
- •Решение нелинейных уравнений
- •Метод половинного деления
- •Интерполяция Постановка задачи интерполяции
- •Кусочно-линейная интерполяция
- •Интерполяционный многочлен Лагранжа
- •Интерполяционный многочлен Ньютона
- •Численное интегрирование Постановка задачи численного интегрирования
- •Формула трапеций
- •Формула Симпсона
- •Погрешности формул численного интегрирования
- •Численные методы решения дифференциальных уравнений первого порядка Постановка задачи
- •Методы Эйлера и Рунге-Кутта решения задачи Коши
- •Аппроксимация методом наименьших квадратов Постановка задачи аппроксимации
- •Формулы метода наименьших квадратов.
- •Варианты заданий для курсовой работы
- •Рекомендуемая литература
- •О г л а в л е н и е
- •Часть 2. “Численные методы”
Аппроксимация методом наименьших квадратов Постановка задачи аппроксимации
Пусть значения функции f(x)известны в точках
x0,
x1,
... ,xn;
f(xi)
= yi.Задача аппроксимации – приблизить
(или, как говорят, аппроксимировать)
функциюf(x)некоторой достаточно близкой функциейy(x).При этом, в отличии от интерполяции, на
функциюf(x)не налагаются требованияy(xi)
=
yi,достаточно лишь, чтобыy(xi)
»
yi.Подобная ситуация возникает, когда сами
значенияyiбыли известны не точно, а лишь приближенно,
и аппроксимирующая функция сглаживает
значенияyi.
Как правило, в качестве меры близости
функцийy(x)
иf(x)берут сумму квадратов их отклонений![]() .
.
В качестве аппроксимирующей функции возьмем ту функцию y(x)из выбранного класса, для которой достигается минимумS. В этом случае говорят об аппроксимации методом наименьших квадратов.
Формулы метода наименьших квадратов.
В качестве аппроксимирующей функции рассмотрим многочлен kйстепени:y(x)=c0+c1x+c2x2+ ...ckxk. Необходимо найти минимум суммы квадратов разностей:
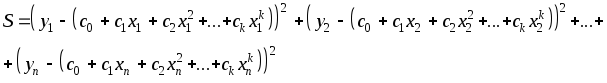 Для
этого продифференцируемSпоc0,
c1,
c2,
...ckи приравняем эти частные производные
нулю.
Для
этого продифференцируемSпоc0,
c1,
c2,
...ckи приравняем эти частные производные
нулю.
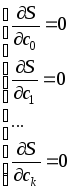
Решив полученную систему уравнений, найдем c0, c1, c2, ...ck, дающие минимумS.
Если аппроксимирующая функция y(x) выбирается среди всевозможных линейных функций, т.е. функций видаy = с0 + с1x, то решение системы может быть получено по следующим формулам:
![]() ,
,![]()
где
![]() ,
,![]() ,
,![]() ,
,![]() .
.

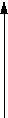













 y
y
Варианты заданий для курсовой работы
Написать программу на языке Паскаль для решения следующей задачи (вариант задания выбирается по последней цифре студенческого билета). Все результаты расчетов должны выводится на экран и в файл.
Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.1), y(0.2) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией в средней точке (в дифференциальном уравненииk = 2). По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
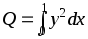 с помощью метода Симпсона.
с помощью метода Симпсона.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.05), y(0.1) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией по средней производной (в дифференциальном уравненииk = 3). По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
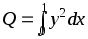 с помощью метода Симпсона.
с помощью метода Симпсона.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.1), y(0.2) ... y(1)с помощью метода Рунге-Кутта четвертого порядка (в дифференциальном уравненииk = 4). По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
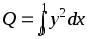 с помощью метода Симпсона.
с помощью метода Симпсона.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.05), y(0.1) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией в средней точке (в дифференциальном уравненииk = 5). По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
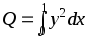 с помощью метода трапеций.
с помощью метода трапеций.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.1), y(0.2) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией по средней производной (в дифференциальном уравненииk = 6По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
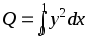 с помощью метода трапеций.
с помощью метода трапеций.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.05), y(0.1) ... y(1)с помощью метода Рунге-Кутта четвертого порядка (в дифференциальном уравненииk = 7). По найденным значениямy определить количество тепла, выделяющееся на единичном сопротивлении за единицу времени, по формуле
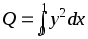 с помощью метода трапеций.
с помощью метода трапеций.Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.25), y(0.5) ... y(1)с помощью метода Эйлера первого порядка. В дифференциальном уравненииk – наименьший положительный корень уравненияx5-8x-1=0, который найти с помощью метода половинного деления, точностьe=0.001.
Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.1), y(0.2) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией в средней точке. В дифференциальном уравненииk – наименьший положительный корень уравненияx5-x3-3=0, который найти с помощью метода половинного деления, точностьe=0.0001.
Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.2), y(0.4) ... y(1)с помощью метода Рунге-Кутта второго порядка с коррекцией по средней производной. В дифференциальном уравненииk – наименьший положительный корень уравнения 2x4-x3-8=0, который найти с помощью метода деления пополам, точностьe=0.001.
Ток в электрической цепи описывается дифференциальным уравнением (см. стр. 24), которое необходимо решить, найдя y(0.25), y(0.5) ... y(1)с помощью метода Рунге-Кутта четвертого порядка. В дифференциальном уравненииk – наименьший положительный корень уравненияx6-4x4-2=0, который найти с помощью метода половинного деления, точностьe=0.0001.
Вариант дифференциального уравнения выбирается по предпоследней цифре студенческого билета.
0.
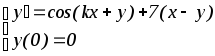 5.
5.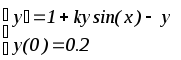
1.
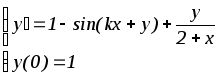 6.
6.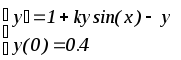
2.
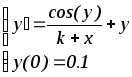 7.
7.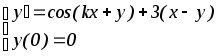
3.
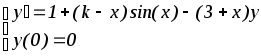 8.
8.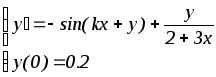
4.
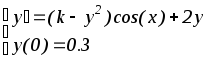 9.
9.