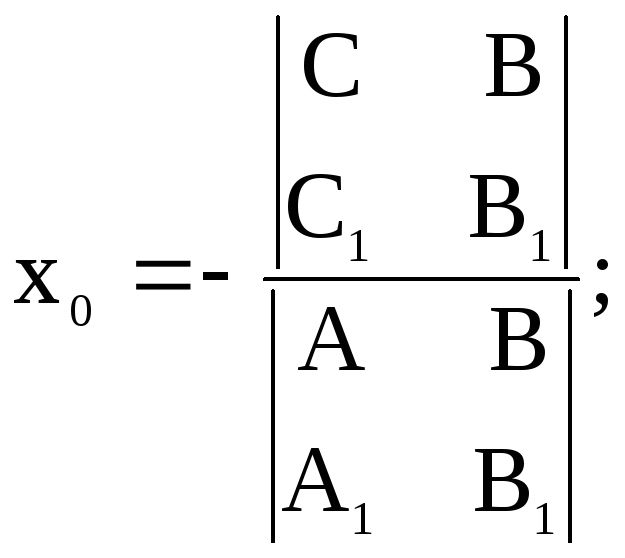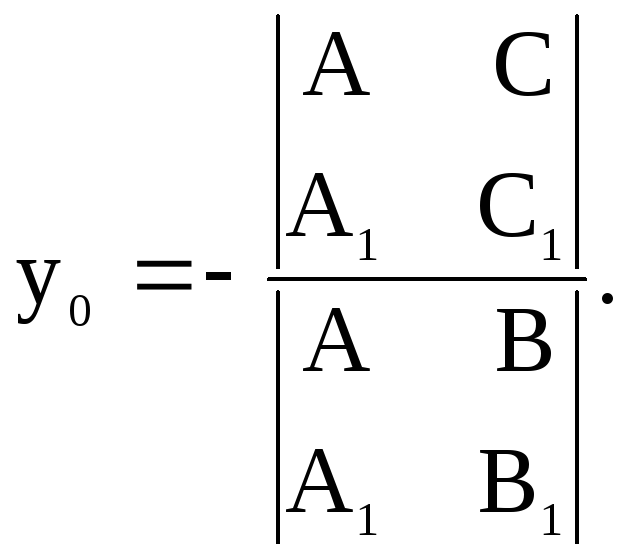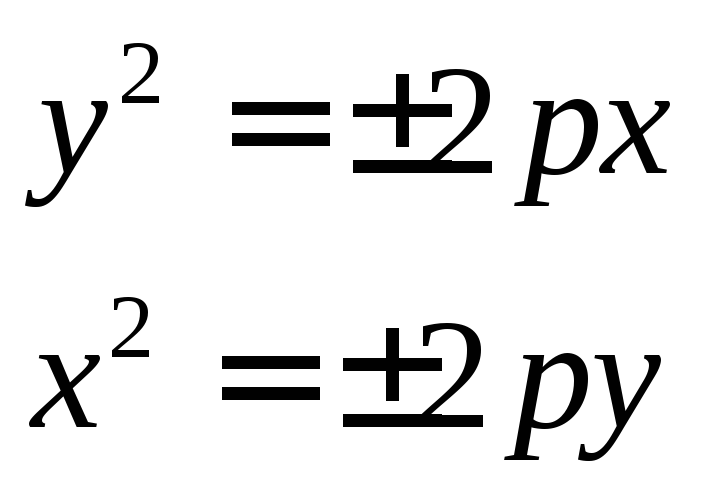- •1 Курс, 1 семестр.
- •Лекция 1. Определители. (рассм. На прк)
- •Свойства определителей (справедливы для определителей любого порядка)
- •Вычисление определителей 4-го и более высоких порядков.
- •Лекция 3. Скалярное, векторное и смешанное произведение векторов и их свойства.
- •Лекция 4. Комплексные числа
- •Линейная алгебра
- •Лекция 5. Матрицы: определения, виды матриц.
- •Действия над матрицами.
- •Основные определения
- •Линейные операции над матрицами
- •Транспонирование матриц и его свойства
- •Лекция 6. Системы линейных алгебраических уравнений и методы их решения (формулы Крамера, матричный метод)
- •Решение систем трех линейных уравнений с тремя неизвестными матричным методом.
- •Лекция 7. Решение систем линейных алгебраических уравнений (слау) методом Гаусса Суть метода Гаусса:
- •Решение однородных слау
- •Лекция 8. Плоскость в пространстве
- •1.1. Общее уравнение плоскости в пространстве
- •1.2. Уравнение плоскости, проходящей через данную точку параллельно двум заданным (неколлинеарным) векторам
- •1.3. Уравнение плоскости, проходящей через три данные точки
- •1.4. Уравнение плоскости «в отрезках»
- •1.5. Нормальное уравнение плоскости
- •1.6. Полярные параметры плоскости
- •1.7. Особые случаи расположения плоскости в пространстве относительно системы координат
- •2. Плоскости в пространстве: взаимное расположение
- •2.5. Угол между плоскостями
- •2.6. Условия параллельности и перпендикулярности плоскостей
- •1.1. Уравнение прямой на плоскости,
- •1.10. Полярные параметры прямой
- •2. Прямые на плоскости: взаимное расположение
- •2.1. Условие, при котором три точки лежат на одной прямой
- •2.2. Взаимное расположение прямой и пары точек
- •2.3. Расстояние от точки до прямой
- •2.4. Пучок прямых
- •2.5. Угол между прямыми
- •2.6. Условия параллельности и перпендикулярности прямых
- •2.7. Точка пересечения непараллельных прямых
- •Лекция 10. Прямая в пространстве
- •Лекция 11. Кривые второго порядка
- •Лекция 12. Поверхности второго порядка
- •Математический анализ
2.6. Условия параллельности и перпендикулярности прямых
Прямые, заданные
общими уравнениями:
![]() и
и![]() взаимно перпендикулярны тогда и только
тогда, когда
взаимно перпендикулярны тогда и только
тогда, когда![]() Данные прямые параллельны тогда и только
тогда, когда
Данные прямые параллельны тогда и только
тогда, когда![]()
Прямые на плоскости,
заданные в виде:
![]() и
и![]() перпендикулярны только том случае,
когда
перпендикулярны только том случае,
когда![]() (при
(при![]() ).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.
).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.![]()
Прямые, заданные
своими каноническими уравнениями:
![]() и
и![]() взаимно перпендикулярны тогда и только
тогда, когда
взаимно перпендикулярны тогда и только
тогда, когда![]() Данные прямые параллельны, если только
выполнено условие:
Данные прямые параллельны, если только
выполнено условие:![]()
2.7. Точка пересечения непараллельных прямых
Если на плоскости
заданы две прямые:
![]() и
и![]() ,
то согласно утверждению 2 координаты
,
то согласно утверждению 2 координаты![]() точки пересечения этих прямых можно
вычислить по формулам:
точки пересечения этих прямых можно
вычислить по формулам:
|
|
(21) |
|
(22) |
Лекция 10. Прямая в пространстве
Общее уравнение прямой
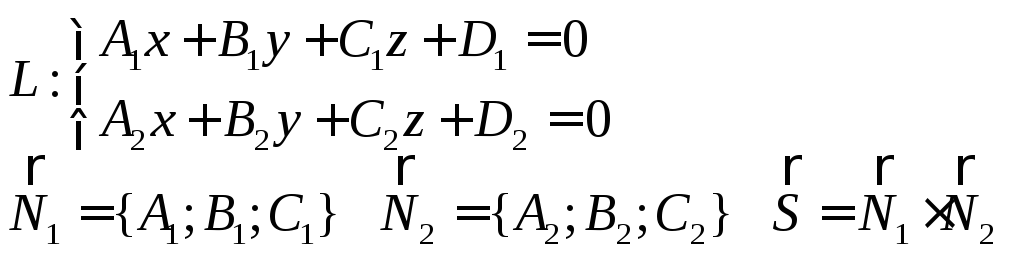
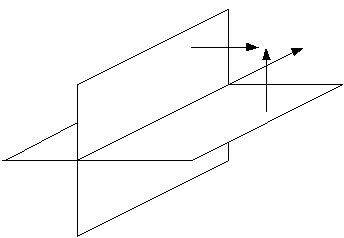
![]() направляющий вектор прямой
направляющий вектор прямой
Каноническое уравнение прямой
![]()
![]()
Параметрические уравнения прямой
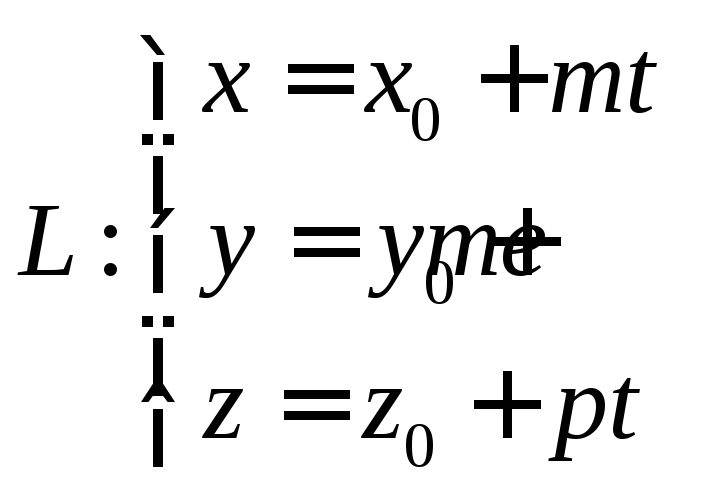
Уравнение прямой проходящей через 2 данные точки
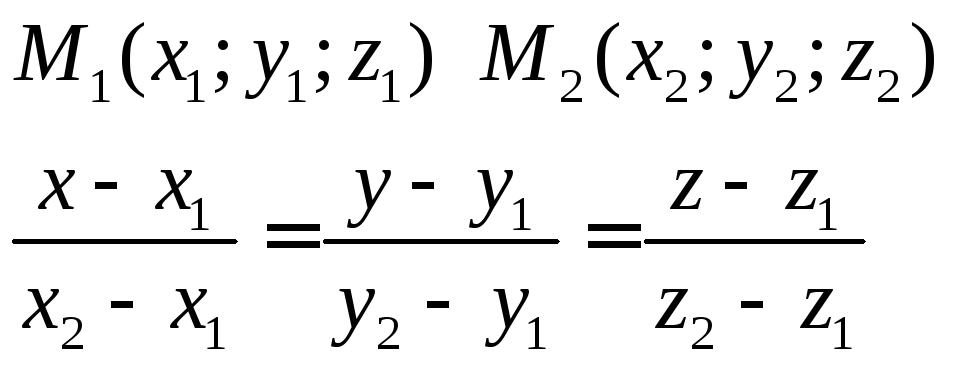
Угол между прямыми
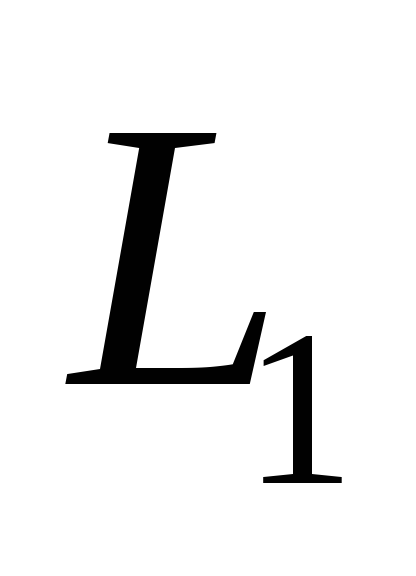 и
и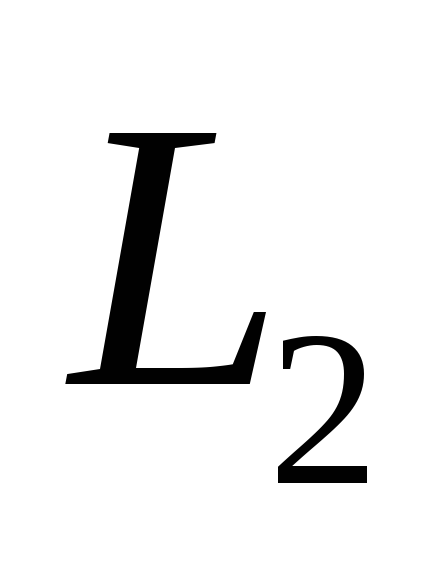
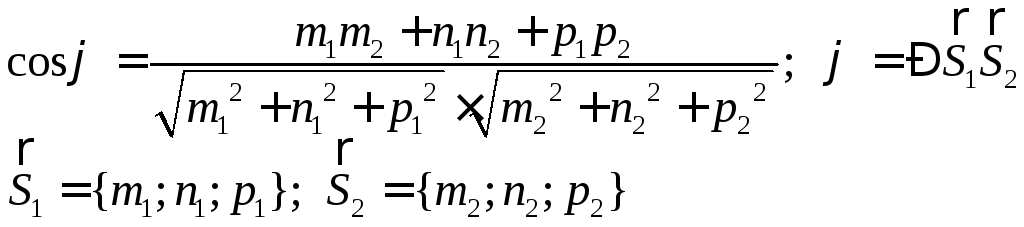
6.
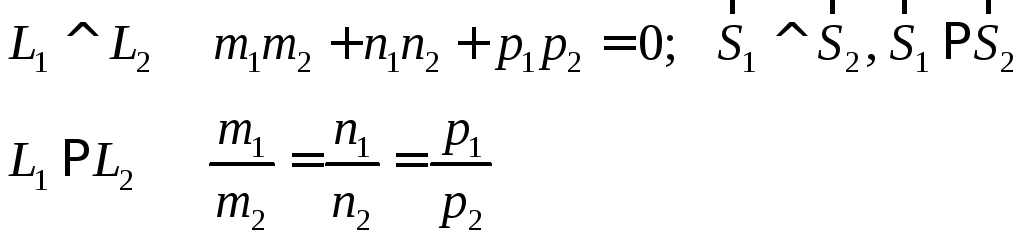
![]() и
и![]() лежат в одной плоскости
лежат в одной плоскости
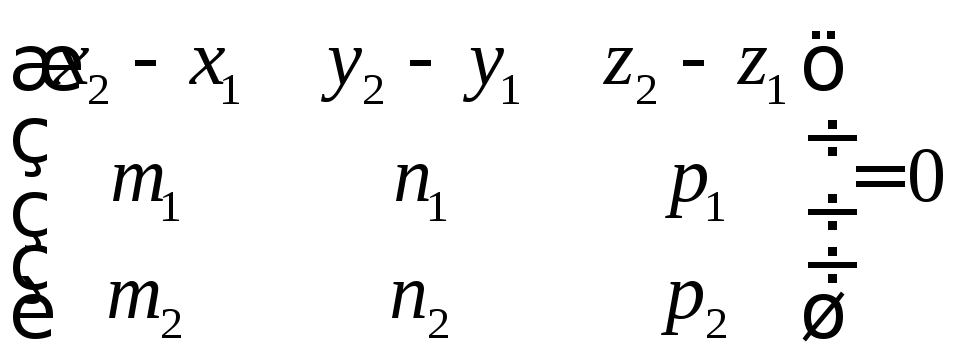
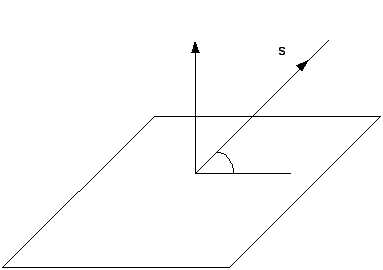
Прямая и плоскость в пространстве
Угол между прямой L и плоскостью

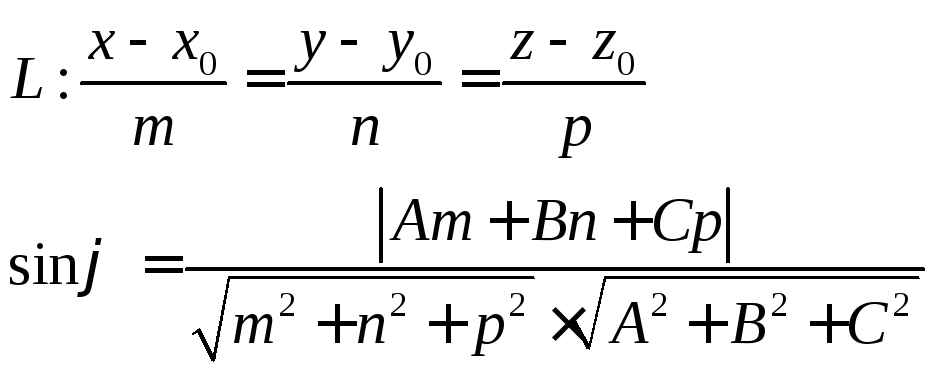
2.
![]()
L-
лежит в
плоскости
![]()
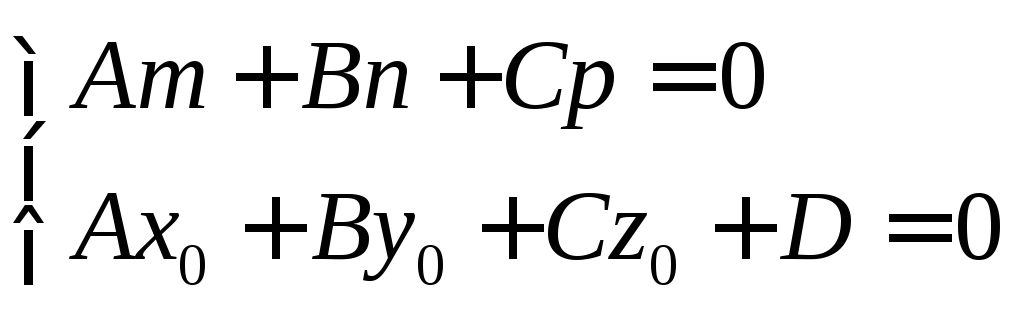
3.
![]() если
если
![]()
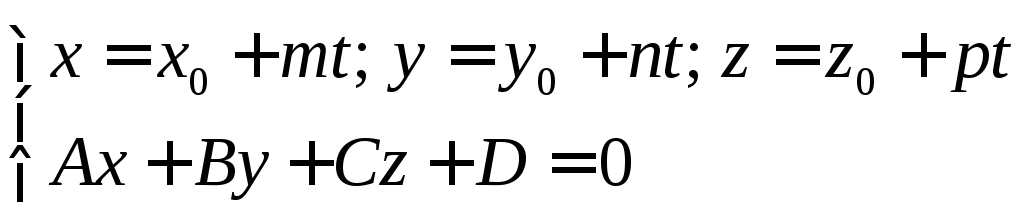
4.
![]()
Лекция 11. Кривые второго порядка
Кривой второго
порядка называется геометрическое
место точек, задаваемых уравнением:
![]() .
В зависимости от вида этой кривой
уравнение можно привести к одному из
канонических, задающему кривую,
принадлежащую одному из классов.
.
В зависимости от вида этой кривой
уравнение можно привести к одному из
канонических, задающему кривую,
принадлежащую одному из классов.
Классификация кривых второго порядка






 Невырожденные Вырожденные
Невырожденные Вырожденные
|
Эллипс |
Гипербола |
Парабола |
Точка (0;0) |
Пара пересекающихся прямых |
Пара совпадающих прямых |
Пара параллельных прямых |
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Каноническое
уравнение
|
Признак вырожденности кривой: уравнение можно представить в виде произведения двух сомножителей.
Эллипс
Кривая второго
порядка, заданная каноническим уравнением
![]() ,
называется эллипсом.a,b
– полуоси
эллипса. Если
,
называется эллипсом.a,b
– полуоси
эллипса. Если
![]() ,
то a-
большая полуось, b-
малая полуось.
,
то a-
большая полуось, b-
малая полуось.
Построение эллипса,
заданного каноническим уравнением
![]() .
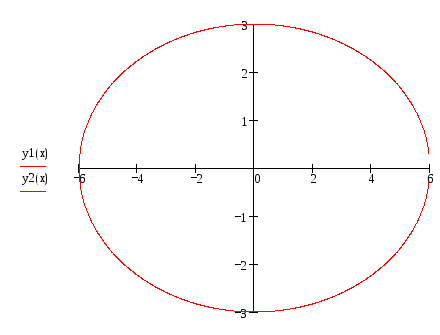
Пусть уравнение эллипса имеет вид
.
Пусть уравнение эллипса имеет вид![]() .
Построим прямыеx=6
и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам
.
Построим прямыеx=6
и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам
![]() если в уравнении
если в уравнении
![]() .
Если
.
Если
![]() ,
то фокусы имеют координаты
,
то фокусы имеют координаты
![]() (эллипс ориентирован вертикально).
(эллипс ориентирован вертикально).
Оптическое свойство эллипса состоит в том, что если точечный источник света поместить в один фокус эллипса, то в другом фокусе появится его изображение.
Эксцентриситет
эллипса – степень его вытянутости
- отношение расстояния от центра эллипса
до фокуса к его большой полуоси,
вычисляется по формуле
![]() .
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением
.
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением
![]() эксцентриситет
эксцентриситет![]() ,
а фокусы находятся в точках
,
а фокусы находятся в точках![]() .
.
Окружность
– частный случай эллипса, задается
уравнением
![]() ,
гдеR
– радиус окружности. У окружности 0,
а фокусы совпадают с центром ( началом
координат).
,
гдеR
– радиус окружности. У окружности 0,
а фокусы совпадают с центром ( началом
координат).
Гипербола
Гипербола
– кривая, задаваемая каноническим
уравнением
![]() или
или![]() .a,b
– полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые
.a,b
– полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые
![]() - асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
- асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
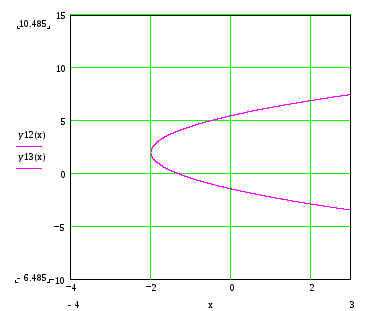
Построение гиперболы
Построение
гиперболы, заданной уравнением начинаем
с отложения по оси Ox
отрезка длиной a
единиц, а по
оси Oy
– длиной b
единиц.
Строим прямые
![]() и
и
![]() .
Гипербола будет касаться полученного
прямоугольника в двух точках
.
Гипербола будет касаться полученного
прямоугольника в двух точках
![]() .
Проведем прямые
.
Проведем прямые![]() - асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
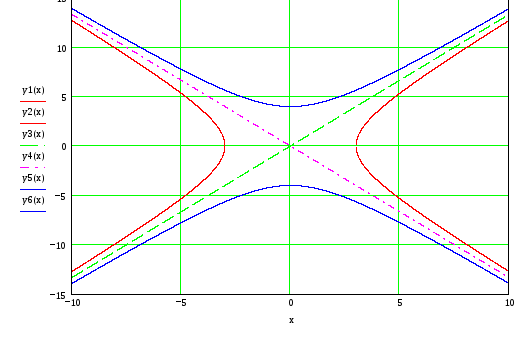
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением
- асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением![]() )
представлен на рисунке. Если в уравнении
гиперболы
)
представлен на рисунке. Если в уравнении
гиперболы![]() поменять знаки передx
и y,
то получим сопряженную ей гиперболу
поменять знаки передx
и y,
то получим сопряженную ей гиперболу
![]() ,
которая имеет те же асимптоты.
,
которая имеет те же асимптоты.
Так же как и эллипс,
гиперболу можно определить как
геометрическое
место точек, разность расстояний которых
от фокусов постоянна.
Фокусы гиперболы имеют координаты
![]() ,
где
,
где
![]() (значенияa,b
берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках
(значенияa,b
берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках
![]() .
.
Оптическое свойство гиперболы состоит в том, что если источник света поместить в один фокус гиперболы, то из бесконечно удаленной точки он будет виден так, как будто он находится во втором фокусе.
Эксцентриситет
гиперболы – степень ее вытянутости.
Для гиперболы
(в общем случае >1)
, задаваемой
уравнением
![]() эксцентриситет
эксцентриситет![]() ,
а фокусы находятся в точках
,
а фокусы находятся в точках![]() .
.
Парабола
Параболой
называется
кривая второго порядка, задаваемая
каноническим уравнением вида
![]() или
или![]() ,
гдеp
– параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
,
гдеp
– параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
Вверх, в случае если уравнение имеет вид
 приp>0.
приp>0.Вниз, в случае если уравнение имеет вид
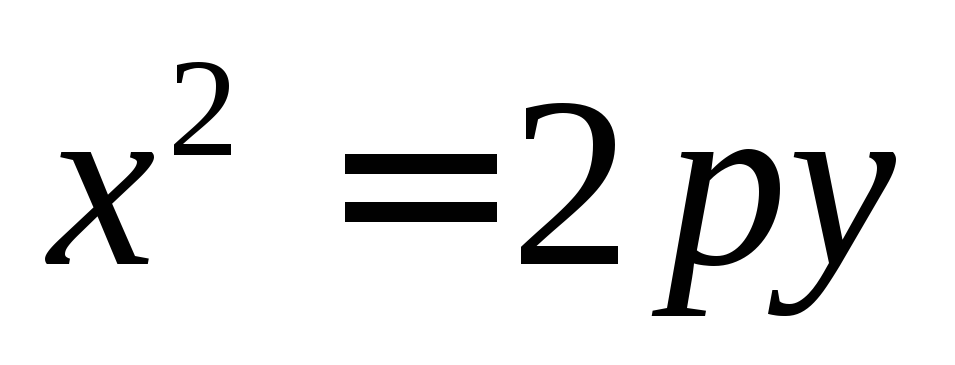 приp<0.
приp<0.Вправо, в случае если уравнение имеет вид
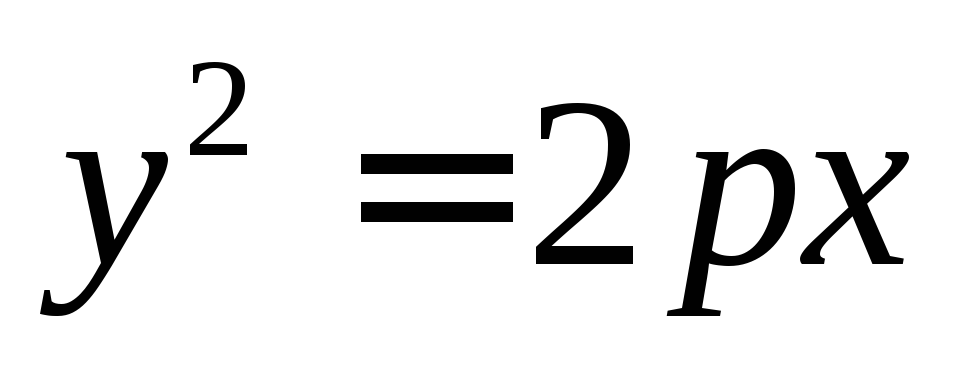 приp>0.
приp>0.Влево, в случае если уравнение имеет вид
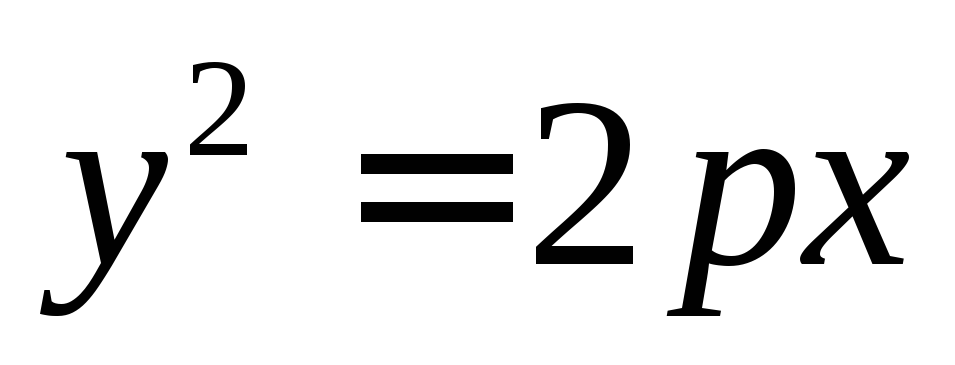 приp<0.
приp<0.
Параболу можно
определить как геометрическое место
точек, равноудаленных от точки
![]() - фокуса - и прямой
- фокуса - и прямой
![]() - директрисы.
- директрисы.
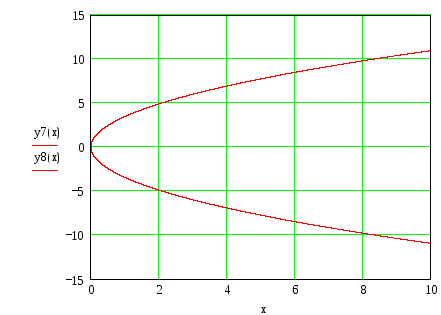
Оптическое свойство параболы состоит в том, что если в фокус параболы поместить точечный источник света, то из нее будет выходить параллельный пучок лучей.
Приведение уравнений кривых второго порядка к каноническому виду.
Общее
уравнение кривой
![]() ,
причем примем ( для упрощения расчетов)B=0.
Существуют два метода преобразования
уравнения общего вида к каноническому:
,
причем примем ( для упрощения расчетов)B=0.
Существуют два метода преобразования
уравнения общего вида к каноническому:
Выделение полного квадрата
Замена переменной
Для данного уравнения замену удобно ввести замену в виде:
![]()
![]() ,
где x’
и y’
– новые переменные.
,
где x’
и y’
– новые переменные.
Если
A
и C
не равны 0, то
![]() - новый центр кривой второго порядка, аx’
и y’
- новые оси.
- новый центр кривой второго порядка, аx’
и y’
- новые оси.
Пример:
1.
Кривая второго порядка задана уравнением
![]() .
Выяснить, чему оно соответствует.
.
Выяснить, чему оно соответствует.
Данному
уравнению соответствует окружность со
смещенным центром, имеющая каноническое
уравнение
![]() ,
где (x0;y0)
– координаты центра окружности, а R
– ее радиус. Воспользуемся
методом выделения полного квадрата для
нахождения канонического вида уравнения.
,
где (x0;y0)
– координаты центра окружности, а R
– ее радиус. Воспользуемся
методом выделения полного квадрата для
нахождения канонического вида уравнения.

Итак, данное уравнение соответствует окружности радиуса 2 ед. с центром в точке (2;0).
Привести уравнение к каноническому виду и построить кривую:
![]()
Воспользуемся методом замены переменных. Имеем:

Получилось каноническое уравнение эллипса с центром в точке (1;-2). Строим его по вышеописанному алгоритму.
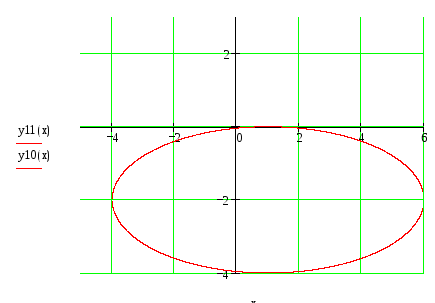
Привести к каноническому виду уравнение
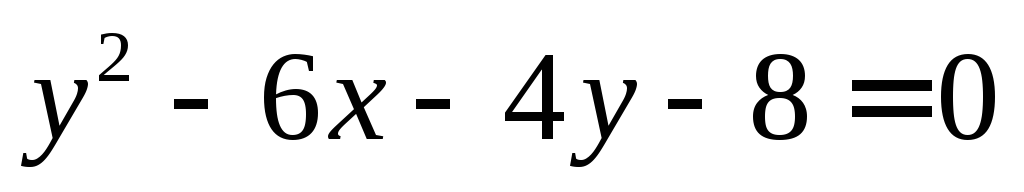 .
Построить кривую, заданную вышеописанным
уравнением.
.
Построить кривую, заданную вышеописанным
уравнением.
Используем метод выделения полного квадрата и замены переменной.
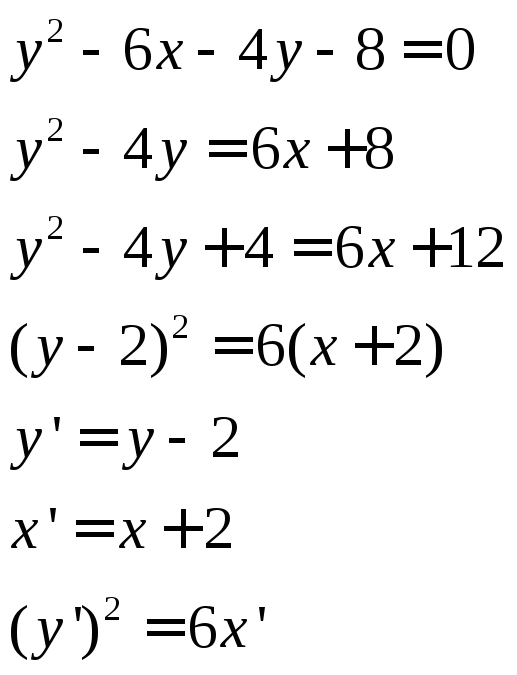
Получилось уравнение параболы с центром в точке (-2;2)