
- •Оглавление
- •Введение
- •Глава 1. Основные показатели макроэкономики
- •1.1. Общественное воспроизводство
- •1.2. Национальное богатство
- •1.3. Система национального счетоводства
- •1.4. Связь между основными показателями макроэкономики
- •1.5. Методы расчета ВВП
- •1.6. Личный и располагаемый доходы
- •1.7. Качество и уровень жизни
- •1.8. Конечное потребление
- •1.9. Коэффициент концентрации Джини
- •1.10. Отраслевая структура национальной экономики
- •1.11. Межотраслевой баланс
- •1.12. Статический межотраслевой баланс
- •1.13. Цены в статической системе межотраслевых связей
- •Упражнения
- •Библиографический список
- •Глава 2. Модели межотраслевого баланса
- •2.1. Схема межотраслевого баланса
- •2.2. Коэффициенты полных материальных затрат
- •2.3. Продуктивная матрица
- •2.4. Динамическая модель межотраслевого баланса
- •2.5. Модель Неймана
- •Упражнения
- •Библиографический список
- •Глава 3. Макроэкономические производственные функции
- •3.1. Понятие макроэкономической производственной функции
- •3.2. Свойства макроэкономической производственной функции
- •3.3. Мультипликативная макроэкономическая производственная функция
- •3.4. Построение производственной функции
- •3.5. Основные характеристики макроэкономической производственной функции
- •3.6. Изокванты и изоклинали
- •3.7. Эффективность и масштаб производства
- •Упражнения
- •Библиографический список
- •Глава 4. Модели потребления
- •4.1. Кейнсианская модель потребления
- •4.2. Модель Фишера
- •4.3. Модель Модильяни
- •4.4. Модель Фридмена
- •4.5. Функция полезности
- •4.6. Линии безразличия
- •4.7. Оптимизация функции полезности
- •4.8. Задача потребительского выбора для произвольного числа товаров
- •4.9. Уравнение Слуцкого
- •4.10. Кривые «доход-потребление»
- •4.11. Кривые «цена-потребление»
- •4.12. Макроэкономические инвестиции
- •4.13. Характеристики инвестиций
- •4.14. Спрос на инвестиции
- •Упражнения
- •Библиографический список
- •Глава 5. Теории экономического роста
- •5.1. Факторы экономического роста
- •5.2. Модель Харрода—Домара
- •5.3. Модель Солоу
- •5.4. «Золотое правило» накопления
- •Упражнения
- •Библиографический список
- •Глава 6. Макроэкономическое равновесие на товарном рынке
- •6.1. Понятие макроэкономического равновесия
- •6.2. Классическая модель макроэкономического равновесия
- •6.3. Модель совокупного спроса
- •6.4. Модель совокупного предложения
- •6.6. Модель «кейнсианский крест»
- •6.7. Мультипликатор автономных расходов
- •6.8. Парадокс бережливости
- •Упражнения
- •Библиографический список
- •Глава 7. Макроэкономическое равновесие на денежном рынке
- •7.1. Сущность и функции денег
- •7.2. Денежная масса
- •7.3. Модель инфляции
- •7.4. Теории спроса на деньги
- •7.4.1. Классическая теория спроса на деньги
- •7.4.3. Кейнсианская теория спроса на деньги
- •7.4.4. Монетаристская теория спроса на деньги
- •7.5. Предложение денег
- •7.6. Равновесие на рынке денег
- •Упражнения
- •Библиографический список
- •Глава 8. Макроэкономическое равновесие на товарном и денежном рынках
- •8.1. Линия инвестиции-сбережения (IS)
- •8.2. Линия предпочтение ликвидности-деньги (LM)
- •8.3. Модель IS—LM
- •8.4. Динамика установления макроэкономического равновесия на совместном рынке
- •8.7. Ликвидная ловушка
- •8.8. Модель совокупного спроса
- •Упражнения
- •Библиографический список
- •Глава 9. Экономические циклы
- •9.1. Понятие экономических циклов
- •9.2. Мировые циклы Кондратьева
- •9.3. Технологические уклады
- •9.4. Особенности циклического развития различных стран
- •9.5. Среднесрочные циклы
- •9.6. Теории экономических циклов
- •9.6.1. Модель Самуэльсона—Хикса
- •9.6.2. Модель Тевеса
- •9.6.3. Модель Гудвина
- •9.7. Практическое использование экономических циклов
- •9.7.1. Прогнозирование
- •9.7.2. Модель Ханса Виссема
- •Упражнения
- •Библиографический список
- •Глава 10. Рынок труда
- •10.1. Понятие рынка труда и рабочей силы
- •10.2. Спрос на труд
- •10.3. Предложение труда
- •10.4. Равновесие на рынке труда и безработица
- •10.5. Безработица и ее характеристики
- •10.6. Модель Оукена
- •10.7. Инфляция и ее виды
- •10.8. Адаптивные и рациональные ожидания
- •10.9. Инфляция и безработица — кривая Филлипса
- •10.10. Антиинфляционная политика
- •Упражнения
- •Библиографический список
- •Глава 11. Рынок ценных бумаг и его инструменты
- •11.1. Понятие рынка ценных бумаг
- •11.2. Анализ характеристик ценных бумаг
- •11.2.1. Технический анализ
- •11.2.2. Фундаментальный анализ
- •11.3. Риск и ограничение риска
- •11.3.1. Хеджирование
- •11.3.2. Мера риска
- •11.4. Индексы деловой активности
- •11.5. Основные характеристики акций
- •11.6. Основные характеристики облигаций
- •11.7. Государственные облигации
- •11.8. Дюрация и изгиб
- •11.9. Форвардные контракты
- •11.10. Паритет покупательной способности
- •11.11. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ
- •11.12. Опционы
- •Упражнения
- •Библиографический список
- •Глава 12. Портфель ценных бумаг
- •12.1. Характеристики портфеля ценных бумаг
- •12.2. Портфель из двух типов ценных бумаг
- •12.3. Оптимальный портфель
- •12.4. Определение состава оптимального портфеля
- •12.5. Определение состава оптимального портфеля в Excel
- •12.6. Оптимальный портфель с добавлением безрисковых ценных бумаг
- •12.7. Алгоритм построения оптимального портфеля ценных бумаг
- •12.8. Рыночный портфель
- •12.9. Эффективный рынок ценных бумаг
- •Упражнения
- •Библиографический список
- •13.1. Фискальная политика государства
- •13.2. Налоговые органы Российской Федерации
- •13.3. Ответственность за налоговые правонарушения в Российской Федерации
- •13.4. Виды налогов
- •13.5. Суммарная выплата по основным налогам
- •13.7. Оптимизация налоговой ставки. Кривая Лаффера
- •13.8. Модель государственного бюджета
- •13.9. Доходы и расходы государственного бюджета
- •13.10. Бюджетный дефицит
- •Упражнения
- •Библиографический список
- •Ответы и решения
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Глава 6
- •Глава 7
- •Глава 8
- •Глава 9
- •Глава 10
- •Глава 11
- •Глава 12
- •Глава 13
98 |
I. Основные характеристики макроэкономики |
Дробь yx называется нормой замены первого продукта вторым,
а производная dydx — предельной нормой замены первого продукта
вторым. Если известна функция полезности u f x, y , то норма
замены рассчитывается по формуле (4.6) и показывает, на сколько должен потребитель увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на 1 единицу без изменения уровня удовлетворения своих потребностей.
4.7. Оптимизация функции полезности
Задачей потребительского выбора называется определение такого потребительского набора x , y , который максимизирует его
функцию полезности при заданном бюджетном ограничении. Этот набор называют оптимальным для потребителя, èëè локальным рыночным равновесием потребителя.
Бюджетным ограничением называется денежная сумма (доход), предназначенная на покупку данного набора товаров. Бюджетное ограничение I и цены на первый товар p1 и второй товар p2 ñâÿ-
заны соотношением p1x p2 y I . При помощи математических символов задачу математического выбора можно записать в виде:
u x, y max
при условиях |
|
|
p1x p2 y I, |
(4.7) |
|
x 0, |
y 0. |
|
Оптимальную точку потребительского набора x , y называют
точкой спроса. Ясно, что координаты точки спроса зависят от цен и бюджетного ограничения I . Функция точки спроса от цен и бюджетного ограничения называется функцией спроса. Для потребительского набора из двух товаров функцией спроса является набор из двух функций:
x x p1, p2, I ; y y p1, p2, I .
4. Модели потребления |
99 |
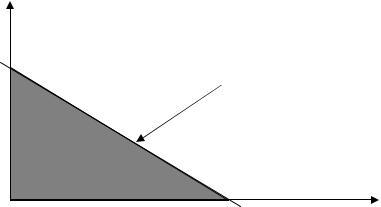
Множество наборов товаров, доступных для потребителя, представляет собой треугольник, ограниченный осями координат и бюджетной прямой p1x p2 y I (ðèñ. 4.8).
y
Бюджетная прямая p1x p2 y I
0 |
x |
|
Ðèñ. 4.8. Бюджетное ограничение |
|
Основные свойства задачи потребительского выбора |
1. |
Решение задачи x , y не изменится при любом монотон- |
ном преобразовании функции полезности u f x, y è ïðè íåèç-
менном бюджетном ограничении. Монотонным преобразованием функции полезности может быть ее умножение на некоторое положительное число, возведение ее в положительную степень, логарифмирование по основанию, большему единицы. При монотонном преобразовании функции полезности ее свойство 1 должно сохраняться, а свойства 2 и 3 могут теряться или приобретаться. То есть, если функция полезности в задаче потребительского выбора не обладает свойствами 2 и 3, она тем не менее может описывать реальное поведение потребителя.
2. Решение задачи потребительского выбора не изменится, если все цены и доход увеличатся (уменьшатся) в одно и то же число раз. Действительно, поскольку цены и доход не входят в функцию полезности, а умножение на положительное число правой и левой частей бюджетного ограничения p1x p2 y I делает его эк-
вивалентным исходному, то задача остается той же, что и первоначально.
100 |
I. Основные характеристики макроэкономики |
||
При решении задачи математического выбора |
(4.7) |
бюджетное |
|
ограничение p1x p2 y I |
будет выполняться в |
âèäå |
равенства |
p1x p2 y I . Это связано с тем, что значение функции полезности увеличивается при увеличении x è y (свойство 1 функции полез-
ности), т.е. максимум лежит на крайних правых и верхних точках (см. рис. 4.8). Таким образом, задачу математического программирования можно заменить задачей на условный экстремум, т.е.
u x, y max
при условиях
g x, y p1x p2 y I 0, |
(4.8) |
|
x 0, |
y 0, |
|
ãäå u x, y — целевая функция; |
g x, y p1x p2 y I |
— функция связи. |
Функция Лагранжа для этой задачи имеет вид:
L x, y, u x, y p1x p2 y I ,
где — множитель Лагранжа.
Составляем систему линейных уравнений, для чего приравниваем нулю первые частные производные функции Лагранжа:
|
L x, y, |
|
|
|
u x, y |
p 0; |
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
x |
|
|
|
|
|
x |
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
L x, y, |
|
|
|
u x, y |
p2 0; |
||||||||
|
|
|
y |
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
L x, y, |
p x |
p |
2 |
y I 0. |
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Умножим первое уравнение на |
p2 , второе — на p1 и вычтем |
|||||||||||||
второе из первого: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x, y |
p |
2 |
|
u x, y |
p 0. |
||||||
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
|
|
|
y |
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, система уравнений для укороченной подозрительной точки функции Лагранжа имеет вид:
u x, y |
|
u x, y |
|
p1 |
; |
(4.9) |
x |
|
y |
p2 |
|||
|
|
|
|
4. Модели потребления |
|
|
|
101 |
|
p1x p2 y I. |
|
|
|
(4.10) |
|
Сопоставив (4.9) ñ (4.5), получим |
y |
|
p1 |
, т.е. норма замены |
|
x |
p2 |
||||
|
|
|
первого продукта вторым равна отношению цены первого продукта
к цене второго. |
|
|
Геометрический |
смысл условного |
экстремума функции |
u f x, y в точке |
x , y состоит в том, что градиенты целевой |
|
функции grad u x*, |
y* и функции связи |
grad g x , y , выходящие |
из точки x , y , обязательно расположены на одной прямой. Эти
градиенты перпендикулярны линии уровня функций |
f x, y |
è ëè- |
||
нии функции связи |
g x, y . Линия уровня функции |
f x, y |
è ëè- |
|
íèÿ |
функции связи |
g x, y , содержащие экстремальную |
точку |
|
x , |
y , касаются в этой точке (рис. 4.9). |
|
|
|
y
0
 p1x p2 y 1 grad g x , y
p1x p2 y 1 grad g x , y
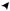 grad u x , y
grad u x , y
x , y
x
Ðèñ. 4.9. Направление градиента целевой функции
и градиента функции связи
Градиент grad u x , y функции u x, y в точке x , y направлен вправо вверх, так как функция полезности u u x, y возрастает в этом направлении (свойство 1).

102 |
|
I. Основные характеристики макроэкономики |
|||||
Градиент grad g x , y функции |
g x, y в точке x , y |
также |
|||||
направлен вправо вверх, так как |
|
|
|
|
|
||
grad g x0, y0 |
g x0, y0 |
i |
g x0, y0 |
j p1i p2 |
j , |
|
|
|
|
|
|||||
|
|
x |
y |
|
|
||
à p1 è p2 |
положительны по условию задачи. |
|
|
||||
Пример 4.3. Функция полезности для двух товаров имеет вид |
|||||||
u xy. |
Бюджетное ограничение I |
и цены на первый товар |
p1 |
||||
и второй товар p2 связаны соотношением p1x p2 y I . |
|
||||||
|
|
|
|
x 0, |
y 0. |
Òàê êàê |
u |
y , à |
u |
x , |
то система уравнений (4.9) è |
|
x |
|
y |
|
|
(4.10) для укороченной подозрительной точки функции Лагранжа имеет вид:
y |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
|
|
|
|
|
p2 |
|
|
|
|
|
||||
x |
|
|
|
y I. |
|
|
|
|||
p x |
p |
2 |
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
Из первого условия следует, что |
x p |
y p |
2 |
, т.е. количество |
||||||
|
|
|
|
|
|
|
1 |
|
|
|
денег, затраченных на оба товара, должно быть одинаковым. Подставив последнюю формулу во второе уравнение системы,
получим x p1 y p2 2I , т.е. расход потребителя на каждый
товар составляет половину общего дохода потребителя. Функция спроса на первый и второй товар приобретает вид:
x 2Ip1 ; y 2Ip2 .
