Кодирование информации
4.1 Кодирование чисел. Системы счисления.
Код - это набор условных сигналов для записи или передачи некоторых заранее определенных понятий (рис.4.1).

Рис. 4.1 Примеры систем кодирования
Любой способ кодирования характеризуется наличием основы(алфавит, спектр цветности, система координат, основание системы счисления…) иправилконструирования информационных образов на этой основе.
Система счисления (СС)- способ кодирования числовой информации, т.е. способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.
Различают системы счисления позиционные и непозиционные. Пример позиционной системы счисления — арабская (современная десятичная), непозиционной — римская (см. табл. 4.1).
Таблица 4.1
|
Позиционная СС |
Непозиционная СС |
|
005 = 5*1 (пять) 050 = 5*10 (пятьдесят) 500 = 5*100 (пятьсот) |
IX = 10-1 = 9 XI = 10+1 = 11 XX = 10+10 = 20 |
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции, разряда). Количество используемых цифр называется основанием системы счисления.
Так, в десятичной системе счисления, основание которой равно 10, различают 10 арабских цифр: 0, 1, 2, ..., 9.
В вычислительной технике широко применяют двоичную, восьмеричную и шестнадцатеричную систему счисления.
Двоичная система счисления имеет основание 2, и, следовательно, ее алфавит состоит из двух цифр - 0 и 1; алфавит восьмеричной системы счисления составляют цифры 0, 1, 2, 3, 4, 5, 6, 7; шестнадцатеричной - десять арабских цифр от 0 до 9 и еще шесть символов - А (10), В (11), С (12), D (13), E (14), F (15).
Для любой позиционной системы счисления справедливо следующее правило формирования n-разрядного числа на основании входящих в эту систему цифр:
 , (4.1)
, (4.1)
где y– число;
q– основание системы счисления;
yi– цифры числа;
i– номер позиции (разряда) числа, начиная с 0.
Системы счисления используются для построения на их основе различных кодов в системах передачи, хранения и преобразования информации.
Код (от лат. codex) — система условных знаков (символов) для представления различной информации.
Любому дискретному сообщению или знаку сообщения можно приписать какой-либо порядковый номер. Измерение аналоговой величины, выражающееся в сравнении ее с образцовыми мерами, также приводит к числовому представлению информации. Передача или хранение сообщений при этом сводится к передаче или хранению чисел. Числа можно выразить в какой-либо системе счисления. Таким образом будет получен один из кодов, основанный на данной системе счисления.
Каждому разряду числа можно поставить в соответствие какой-либо параметр электрического сигнала, например амплитуду. На рис. 4.2 в качестве примера приведено изображение числа 35 в виде импульсов длительностью τ с разными амплитудами (при разных системах счисления).
Анализ систем счисления и построенных на их основе кодов с позиций применения в системах передачи, хранения и преобразования информации показывает, что чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а, следовательно, и меньшее время для его передачи.
Однако с ростом основания существенно повышаются требования к аппаратуре формирования и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.
|
Основание |
12 |
10 |
8 |
4 |
3 |
2 |
|
Запись числа (Код числа) |
2В |
35 |
43 |
203 |
1022 |
100011 |
|
Электрические сигналы (кодовая комбинация) |
|
|
|
|
|
|
Рис. 4.2 Изображение числа 35 в виде сигналов при различных системах счисления
С учетом этих обстоятельств в качестве показателя эффективности системы может быть выбрано число, равное произведению количества различных символов q на количество разрядов N для выражения любого числа. Тогда наиболее эффективной будет система, обеспечивающая минимум значения данного показателя.
Обозначим произведение основания системы q на длину разрядной сетки N, выбранную для записи чисел в этой системе, через С:
С = qN. (4.2)
Если принять, что каждый разряд числа представлен не одним элементом с q устойчивыми состояниями, a q элементами, каждый из которых имеет одно устойчивое состояние, то показатель (4.2) определит условное количество оборудования, которое необходимо затратить на представление чисел в этой системе. В связи с этим показатель (4.2) называют показателем экономичности системы.
Максимальное число, которое можно изобразить в системе с основанием q:
Aq max=qN-1. (4.3)
Из (4.3) можно найти требуемую длину разрядной сетки:
N=logq(Aq max+1). (4.4)
Тогда для любой системы счисления С=q logq(Aq max+1).
Допустим, что величина q является непрерывной величиной. При этом будем рассматривать величину С как функцию от величины q. Теперь если за единицу измерения оборудования принять условный элемент с одним устойчивым состоянием, то для сравнения двух систем счисления можно ввести относительный показатель экономичности:
F= q logq(A2max+1)/[2log2(A2max+1)], (4.5)
позволяющий сравнить любую систему счисления с двоичной.
По правилу приведения логарифмов loga(b)=logc(b)/logc(a) получим:
F=(q∙ln(2))/(2∙ln(q)). (4.6)
На рис. 4.3 представлена зависимость величины F от основания системы счисления q, если функция F непрерывна. Нижняя точка графика соответствует минимуму функции F, определяемому из условия dF/dq=0, что соответствует значению q=e≈2,72.

Рис. 4.4 Зависимость относительного показателя экономичности
от основания системы счисления
Следовательно, с точки зрения минимальных затрат условного оборудования наиболее экономичной является система счисления с основанием 3. Незначительно уступают ей двоичная и четверичная. Системы с основанием 10 и более существенно менее эффективны.
Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение в настоящее время отдается двоичной системе счисления. Действительно, логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов сводится в этом случае к задаче обнаружения (есть импульс или его нет), что значительно проще. Арифметические и логические действия также легче осуществляются в двоичной системе.
Таким образом, для представления любого числа достаточно алфавита, состоящего только из двух символов, что и реализуется при хранении информации в памяти электронных устройств. Ячейка памяти в этом случае может находиться в одном из двух состояний, которые кодируются как 0 и 1. Информационная емкость такой ячейки равна 1 биту.
Число, записанное в позиционной системе счисления с любым основанием, переводится в десятичную систему счисления по правилу (4.1).
Пример:
A(10)=552,25=5102 +5101+ 2100 + 210-1 +510-2
В десятичном числе A(10) цифры 5 и 2, находящиеся на разных позициях, имеют различные количественные значения, при перемещении цифры на следующую позицию ее величина изменяется в 10 раз.
A(10) = 102,839 = 1102 + 0101 +2100 +810-1 +310-2 +910-3
Если вместо 10 взять любое другое натуральное число p > 1, легко построить число в системе счисления с основанием p.
Пусть, например, p = 2. В этой двоичной системе счисления употребляются только две цифры: 0 и 1.
11011,011(2) = 124 + 123 + 022 +121 +120 + 02-1 + 12-2 = 27,375(10)
Каждое целое число может быть записано в системе десятичных цифр, т.е. в виде
A(10)= an10n + an-110n-1 + …+a2102 + a1101 +a0 100,
где n – некоторое соответствующее неотрицательное число; числа an, an-1, …, a2, a1, a0 — знаки цифр из алфавита аi {0…9}.
Запись некоторого числа в другой системе чисел. Любое число в позиционной системе счисления при любом основании q > 1 может быть записано в естественной форме

может быть представлено степенным рядом

 ,
,
где аk — любая цифра из алфавита системы основания p, m, 1 — число позиций (разрядов) соответственно для целой и дробной частей числа. Для удобства преобразования чисел из одной системы счисления в другую степенной ряд для целой и дробной частей числа представляется эквивалентными выражениями по схеме Горнера:
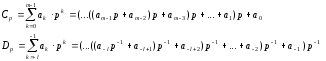
Счет в различных системах счисления. Счет в различных системах счисления производится от нуля, последовательно прибавляя по единице до тех пор, пока число не достигнет величины очередной степени основания системы. В этом случае единица прибавляется к более старшему разряду, для которого правила выполняются аналогично. Операцию счета в различных системах можно проследить по приведенной ниже таблице. Читателю предлагается заполнить пустые клетки в таблице.
Прибавление единицы к более старшему (k+1)–му разряду происходит, когда число, составленное из оставшихся более младших k разрядов составляет pk - 1.
Пример: p = 2, число 0111(2)+1 дает переход единицы из нулевого разряда в первый (в нулевом разряде остался 0), далее из первого во второй (в первом разряде остался 0), и далее в третий, в результате чего получится число 0111(2) + 1 = 7(10) +1 = 8(10) = 23 = 1000(2), k = 3.
|
p=10 |
p=2 |
p=3 |
p=4 |
p=5 |
p=6 |
p=7 |
p=8 |
p=9 |
p=16 |
p=27 |
|
0 |
0000 |
0000 |
0000 |
0000 |
|
000 |
00 |
000 |
0 |
0 |
|
1 |
0001 |
0001 |
0001 |
0001 |
|
|
01 |
|
1 |
1 |
|
2 |
0010 |
0002 |
0002 |
0002 |
|
|
02 |
|
2 |
2 |
|
3 |
0011 |
0010 |
0003 |
|
|
|
03 |
|
3 |
3 |
|
4 |
0100 |
0011 |
0010 |
0004 |
|
|
04 |
|
4 |
4 |
|
5 |
0101 |
0012 |
0011 |
|
|
005 |
05 |
|
5 |
5 |
|
6 |
0110 |
0020 |
0012 |
0011 |
|
|
06 |
|
6 |
6 |
|
7 |
0111 |
0021 |
0013 |
|
|
010 |
07 |
|
7 |
7 |
|
8 |
1000 |
0022 |
0020 |
|
|
|
010 |
008 |
8 |
8 |
|
9 |
|
0100 |
|
|
|
|
|
010 |
9 |
9 |
|
10 |
|
0101 |
|
0020 |
|
013 |
|
|
A |
A |
|
11 |
|
0102 |
|
|
|
|
|
|
B |
B |
|
12 |
|
0110 |
|
|
|
|
|
|
C |
C |
|
13 |
|
0111 |
|
|
|
016 |
|
|
D |
D |
|
14 |
|
0112 |
|
|
|
|
|
|
E |
E |
|
15 |
01111 |
0120 |
0033 |
0030 |
|
|
017 |
|
F |
F |
|
16 |
|
|
|
|
|
|
|
017 |
10 |
G |
|
17 |
|
|
|
|
|
023 |
|
|
12 |
H |
|
18 |
|
|
|
|
|
|
|
|
13 |
I |
|
19 |
|
|
|
0034 |
|
|
|
|
14 |
J |
|
20 |
|
|
|
|
|
|
|
|
15 |
K |
|
21 |
10101 |
|
|
|
|
|
|
024 |
16 |
L |
|
22 |
|
|
|
|
|
|
|
|
17 |
M |
|
23 |
|
|
|
|
|
|
|
|
18 |
N |
|
24 |
|
|
|
0044 |
|
|
|
|
19 |
J |
|
25 |
|
|
|
|
|
|
|
|
1A |
P |
|
26 |
|
|
|
|
|
|
|
|
|
Q |
|
27 |
11011 |
|
|
|
|
|
|
|
|
10 |
Для проверки правильности заполнения пустых клеток необходимо выполнить обратный перевод записанных чисел. Для этого нужно использовать формулу для перевода числа из системы счисления с основанием p в систему счисления с основанием 10 следующим образом. Вписанное число 221(3) =
= A(10) = 232+231+130 = 25, что соответствует числу, расположенному в соответствующей ячейке десятичной системы счисления.
Перевод чисел с основаниями, являющимися степенью другой системы. Если между основаниями p и q соблюдается связь р1 = qk , где k – целое, то каждая цифра числа с основанием p представляется k цифрами алфавита основания q. Так, если p1 = 81 = qk = 23 или
p1 = 271 = qk = 33 то каждая цифра p–го числа (восьмеричного или двадцатиcемиричного) представляется k (тремя) цифрами q–ричного (двоичного или троичного) числа и наоборот — каждая группа из k цифр (от запятой влево и вправо) q–ричного числа заменяется одной p–ричной цифрой (см. в таблице столбцы, выделенные жирным шрифтом и выделенные другим шрифтом).
Примеры. Используя приведенную выше таблицу соответствия чисел в различных системах счисления и выбирая столбцы, выделенные жирным шрифтом или курсивом, выполним перевод.
А(8) = 407,15 = A(2)=100 000 111,001 101 и обратно А(2)=10 011 011,010 11 = =A(8)= 233,26.
B(27) = 23D,23 = B(3)=2 010 111,002 01 и обратно B(3) = 210110,22102 = B(9) = =713,836.
B(9) = 78.457 = B(3) = 2122.111221 и обратно B(3) = 221221001.12021 = B(27) = =PP1.FK
C(16) = 4F0E,1C = С(2) = 0100111100001110,00011100;
C(2)= 11001101011,111101 = C(16) = =66B,F4
Нули перед старшим разрядом целой части и после младшего разряда дробной части можно не записывать.
Такие преобразования используются для сокращения записи двоичных чисел, при переводе чисел из десятичной системы счисления в двоичную, а также при выполнении некоторых операций в ЭВМ.
Перевод целых чисел из одной системы счисления p в другую систему с основанием q. Целое число в системе счисления p может быть представлено эквивалентным числом в системе счисления q:
Ap = Aq = (…((bn-1q + b n-2)q + bn-3)q +… +b1)q + b0
Задача перевода числа из одной системы счисления (p) в другую (q) заключается в отыскании значений цифр bk числа в новой системе счисления.
Заметим, или Аp = Аq = (Аq)1q + b0, где (Аq)1 — целое частное, полученное при делении Аp на основание q, b0 – остаток, являющийся первой младшей цифрой числа в новой системе счисления, выражен цифрами исходной системы счисления.
При следующем делении частного на основание q будут получены новое целое частное и новый остаток: Аp = Аq = (Аq)2q + b1, где b1 - вторая младшая цифра числа. Продолжая деление целых частных до нулевого значения, находят все цифры числа в новой системе.
Правило перевода целого числа из одной системы счисления в другую.
Пусть дано число А в системе счисления p. Для перевода его в систему счисления q необходимо последовательно делить данное число и получаемые целые частные на основание новой системы счисления, выраженные цифрами исходной системы (p), до тех пор, пока частное не станет равным нулю.
Полученные остатки, являющиеся цифрами числа в новой системе счисления, следует выразить цифрами алфавита этой системы.
Составить число в новой системе, начиная с последнего остатка.
Примеры.
Перевести число А(10)= 53 в А(2) .
|
53 53(10) = 110101(2) = =125 +124 +023 +122 + 021 + 120 = =32 + 16 + 0 + 4 + 0 +1 = 53(10) |
2 |
|
|
|
|
|
|
52 |
26 |
2 |
|
|
|
|
|
1 |
26 |
13 |
2 |
|
|
|
|
|
0 |
12 |
6 |
2 |
|
|
|
|
|
1 |
6 |
3 |
2 |
|
|
|
|
|
0 |
2 |
1 |
2 |
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
1 |
|
Перевести число А(10)= 53 в А(8), а затем в А(2).
|
53 53(10) = 65(8) = 681 + 580 = =48 +5 = 53(10) |
8 |
|
|
48 |
6 |
8 |
|
5 |
0 |
0 |
|
|
6 |
|
Перевод восьмеричного числа в двоичное проще выполнить, учитывая, что основание 8 является кубической степенью основания 2. Поэтому достаточно каждый разряд восьмеричного числа представить тремя разрядами двоичного числа: 65(8)=110101(2).
Перевести число А(10)= 53 в А(16), а затем в А(2).
|
53 53(10) = 35(16) = 3161 + 5160 = 48 +5 = 53(10) |
16 |
|
|
48 |
3 |
16 |
|
5 |
0 |
0 |
|
|
3 |
|
Перевод шестнадцатеричного числа в двоичное проще выполнить, учитывая, что основание 16 является четвертой степенью основания 2. Поэтому достаточно каждый разряд восьмеричного числа представить четырьмя разрядами двоичного числа: 35(16)=00110101(2).
Перевести число А(3)= 22 в А(2).
|
22 22(3) = 231 + 230 = 8(10) = 1000(2) = =123 + 022 +021 + 020 = 8(10) |
2 |
|
|
|
|
22 |
11 |
2 |
|
|
|
0 |
11 |
2 |
2 |
|
|
|
0 |
2 |
1 |
2 |
|
|
|
0 |
0 |
0 |
|
|
|
|
1 |
|
Перевести число А(4)= 33 в А(8).
Основание 8 в системе счисления с основанием 4 будет представлено числом 20(4).
20(4)
|
33 33(4) = 17(8) |
20 |
|
|
20 |
1 |
20 |
|
13(4) 7(8) |
0 |
0 |
|
|
1 |
|
Перевести число А(2)= 11010 в А(10).
Воспользуемся основной формулой позиционной системы чисел.
11010 (2) = 124 + 123 + 022 +121 + 020 = 116 + 18 + 04 + 12 + 01 = 26(10)
Перевод дробных чисел из одной системы счисления в другую. Дробная часть числа по схеме Горнера представлена в виде:

Действуя аналогично переводу целой части числа, но, используя операцию умножения, получим правило перевода дробных чисел.
Правило перевода дробных чисел из системы счисления с основанием p в систему счисления с основанием q:
Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы, выраженное цифрами исходной системы, до тех пор, пока дробная часть произведения не станет равной нулю.
Полученные целые части произведений, являющиеся цифрами числа в новой системе, выразить цифрами алфавита этой системы.
Составить дробную часть числа в новой системе, начиная с целой части первого произведения.
Пример. Перевести число А(10)= 0,65625 в А(2) различными способами, используя перевод непосредственно в двоичную систему, а также через восьмеричную и шестнадцатеричную системы.
а) А(10) А(2) б) А(10) А(8) А(2) в) А(10) А(16) А(2)
|
0, |
65625 |
|
|
2 |
|
1, |
31250 |
|
|
2 |
|
0, |
62500 |
|
|
2 |
|
1, |
25000 |
|
|
2 |
|
0, |
50000 |
|
|
2 |
|
1, |
00000 |
|
А(2) = 0,10101 | |
|
0, |
65625 |
|
|
8 |
|
5, |
25000 |
|
|
8 |
|
2, |
00000 |
|
А(2) = 0,53(8)= =0,10101(2) | |

В рассмотренном примере число представляется конечным числом двоичных знаков после запятой. Если же число не представляется конечным числом обратных степеней основания системы, то оно будет представляться бесконечной периодической дробью в этой системе. Отсюда возникает проблема представления числа в ограниченной разрядной сетке памяти компьютера.
Например, число А(10) = 0,3 в двоичной системе представляется бесконечной периодической дробью 0.01001100110011….= 0,0(1001)(2).
Перевод чисел из любой системы счисления p в десятеричную систему чисел. Перевод чисел в десятичную систему может выполняться либо по правилам перевода, либо по формулам степенного ряда, либо по формулам разложения по схеме Горнера. Рассмотрим последовательно применение этих алгоритмов на примерах.
Перевести число А(2)= 10101101 в А(10).
Выполним перевод по правилу перевода целого числа. Для этого представим новое основание системы 10 в двоичной системе: 10(10)= 1010(2), и будем делить двоичное число на новое основание следующим образом:
|
|
10101101 |
1010 |
|
|
|
10101101(2)=173(10) |
1010 |
10001 |
1010 |
|
|
|
1101 |
1010 |
1 |
1010 |
|
|
1010 |
111 |
0 |
0 |
|
|
0011 |
|
1 |
|
0011(2) = 3(10)
111(2) = 3(10)
По формуле степенного ряда перевод А(2)= 10101101 в А(10) производится следующим образом:
10101101(2)= 127+ 026 + 125+024 + 123 + 122 +021 + 120 =
= 1128 + 064 + 132+ 016+ 18 +14+ 02+ 11 = 173(10)
Перевод А(2)= 10101101 в А(10) по формуле Горнера:
((((((12+0)2+1)2+0)2+1)2+1)2+0)2+1=173(10)
Перевести дробные числа А(2)= 0,10101; B(8)= 0,52; C(16) = 0,A8 в десятичную систему различными способами.
Перевод по формуле степенного ряда:
А(2)= 0,10101=12 -1+ 02 -2 + 12 -3+02 -4 + 12 -5 = 0,5+0,125+0,03125 = =0,65625;
В(8)=0,52=58-1+ 28–2=0,625+0,03125= 0,65625;
С(16)=0,А8=1016–1 + 816–2=0,625+0,03125= 0,65625;
Перевод по схеме Горнера:
A = ((((12-1+0)2-1+1)2-1+0)2-1+1)2-1=0,65625(10);
B = (58-1+2)8-1=0,65625(10);
C = (1016-1+8)16-1=0,65625(10);
Выполним перевод по правилу перевода дробного числа. Для этого представим новое основание системы 10 в двоичной системе: 10(10)=1010(2), в восьмеричной системе: 10(10)=12(8), в шестнадцатеричной системе: 10(10)=А(16). Умножение и сложение производится в соответствующей системе.

Арифметические операции в системе чисел
Посмотрим, как проводятся расчеты в другой системе чисел. Пусть основанием системы чисел является цифра 6. Вначале рассмотрим операции с «однозначными» числами. (Однозначными в данном случае будут числа 0, 1, 2, 3, 4, 5.) Этим основным операция нужно учиться, как таблице умножения.
Сложение. Если одним членом некоторой суммы является 0, то сумма равна второму члену. Поэтому суммирование с нулем не рассматривается в силу очевидности.
Построим таблицу сложения однозначных чисел. В первом столбце и первой строке записаны цифры, составляющие алфавит шестеричной системы, кроме 0; на пересечении i-ой строки и j-го столбца находится сумма ai и aj , представленная в шестеричной системе.
Получается следующая таблица:
|
+ |
1 |
2 |
3 |
4 |
5 |
|
1 |
2 |
3 |
4 |
5 |
10 |
|
2 |
3 |
4 |
5 |
10 |
11 |
|
3 |
4 |
5 |
10 |
11 |
12 |
|
4 |
5 |
10 |
11 |
12 |
13 |
|
5 |
10 |
11 |
12 |
13 |
14 |
Например, сумма 3 и 5 находится на пересечении строки с цифрой 3 и столбца с цифрой 5: 3(6) + 5(6) = 12(6).
А теперь посмотрим, как осуществляется суммирование многозначных чисел в той же системе счисления с основанием 6.
Определим сумму 315 + 543. Пусть эти числа записываются в виде:
315 = 3100 + 110 + 5 и 543 = 5100 + 410 + 3.
(Здесь числа 10 и 100 обозначают числа в шестеричной системе чисел.)
Учитывая коммутативность и ассоциативность операции сложения, и используя дистрибутивное свойство, получим форму:
315 + 543 = (3 + 5) 100 + (1 + 4) 10 + (5 + 3).
Найдем значение последнего сложения из таблицы: 5 + 3 = 12 = 110 + 2. Откуда:
315 + 543 = (3 + 5) 100 + (1 + 4 + 1) 10 + 2.
Рассмотрим опять последний член, содержащий операцию сложения. Эта сумма составляется на основе таблицы: (1 + 4) + 1 = 5 + 1 = 10, поэтому:
315 + 543 = (3 + 5 + 1) 100 + 010 + 2.
Если еще раз посмотреть последний член, содержащий операцию сложения: 3 + + 5 +1 = 3 + 10 = 13 = 110 + 3, то получится выражение:
315 + 543 = 11000 + 3100 + 010 + 2 = 1203 .
Процессом сложения доказывается, что применяется такой же метод, как и при сложении в десятичной системе чисел, поэтому операция сложения здесь также может быть осуществлена с помощью записи отдельных чисел друг под другом:
315
+543
1302
Легко видеть, что и сложение большего количества членов, и операция вычитания осуществляются подобно тому, как это делается в десятичной системе чисел.
Умножение. В таблице умножения в системе счисления с основанием 6 представлены произведения однозначных чисел. Умножение на 0 и здесь не следует отдельно записывать, так как в случае, когда один из сомножителей 0, то и результат всего произведения будет 0. Аналогично не нужно приводить произведения, одним из сомножителей которых является 1, так как в этих случаях результат произведения всегда равняется другому сомножителю.
Таблица умножения в системе счисления с основанием 6 имеет следующий вид:
|
|
2 |
3 |
4 |
5 |
|
2 |
4 |
10 |
12 |
14 |
|
3 |
10 |
13 |
20 |
23 |
|
4 |
12 |
20 |
24 |
32 |
|
5 |
14 |
23 |
32 |
41 |
Также при пересечении соответствующей строки и соответствующего столбца можно получить результат произведения. Например, 35 = 23. Действительно:
3 5 = 5 + 5 + 5 = 5 + (1 + 4) + (2 + 3) =
= (5 + 1) + (4 + 2) + 3 = 10 + 10 + 3 = 23.
С помощью таблицы умножения также может быть определено произведение многозначных чисел. Посмотрим, например, как определяется произведение двух шестеричных чисел 315 и 543. Разложим оба числа на множители:
315543 = (3100 + 110 + 5) (5100 + 410 + 3).
На основе дистрибутивного свойства операции данное произведение разлагается таким образом:
315543 = (3100 + 110 + 5)5100 + (3100 + 110 + 5)410 + (3100 + +110+5)3.
В конечном итоге следует вычислить три произведения, а затем полученные произведения суммировать.
Рассмотрим сначала последнее слагаемое. Используя дистрибутивное и ассоциативное свойство, а также коммутативность операции умножения, получим следующее выражение:
(3100 + 110 + 5) 3 = (33) 100 + (13) 10 + (53).
Определив отдельные произведения из таблицы умножения, получим:
3153 = 13100 + 310 + 23 = 1300 + 30 + 23 = 1353.
В предпоследнем члене приходится определить результат умножения 315410. Произведение первых двух сомножителей 2112, все произведение 211210 = 21120. Таким же образом определим первое слагаемое: 243100. Сложение отдельных произведений осуществляется по способу, приведенному выше:
Знаки 0 в конце отдельных чисел могут быть пропущены, но оговаривается, что каждое частное произведение записывается левее на одно место. Если записать все произведение, получится следующее:
1353
21120
+243100
310013
315*543
1353
2112
2431
310013
После этого следует осуществить сложение частных произведений. Последняя цифра записывается без изменения. Делая шаг на одну позицию влево: 5+2=11, записывается последняя цифра 1 и остается 1. Делая шаг влево еще раз на одну позицию, 3+1+1=5, прибавляя остаток: 5 + 1 = 10, записывается 0, остается 1. Шагая влево опять на одну позицию: 1+1+3=5, прибавляя остаток: 5+1=10, записывается 0 и остается 1. Опять делаем шаг влево на одну позицию: 2+4=10, прибавляя остаток: 10+1=11, записывается 1, остается 1. Наконец, прибавляя остаток к первому знаку: 2+1= 3, записывается 3.
Значения произведений и сложений однозначных чисел выписываются из таблиц, приведенных выше.
Деление как повторное вычитание. Операция деления может быть выполнена в виде повторного вычитания. Пусть делится, например, число 3440314 на 512. (Числа шестеричной системы.) Вместо того чтобы брать в качестве делимого числа 512, 2512, , целесообразно рассматривать числа 512, 5120, 51200, 512000, 5120000, Как видно, последнее число уже больше, чем делимое, но предпоследнее — еще меньше. Поэтому число 3440314 делится на 512000; итак, вычитание осуществляется не шагами в 1, а шагами в 1000. Поскольку в делителе стоит 0 на последних трех местах, то неважно, что стоит на последних трех местах делимого; проще всего будет записать туда также знаки 0. Следовательно, сейчас число 3440000 делится на 512000. На самом деле рассматривается деление 3440:512, так как сокращение на 1000 не меняет результата частного. Выполняя операцию деления с остатком, получим:
3440 - 4512 = 3440 - 3252 =144.
Таким образом, 3440314 - 4512000 = 3440000 – 3252000 + 314 = 144000 + 314 = =144314.
Теперь уже только число 144314 приходится делить на 512. Так как данное число меньше, чем 512000, оно делится на 51200, точнее, делится даже не число 144314, а число 144300. Подобно предыдущему случаю, вместо настоящего деления проводится деление числа 1443 на 512. Из операции деления с остатком получится результат: 1443 –2512 = 1443 – 2512 = 15, то есть:
144314 – 251200 = 144300 – 142400 + 14 = 1500 + 14 = 1514.
Далее число 1514 делится на 5120, точнее, делится число 1510, т.е. вместо этого число 151 делится на 512. Очевидно, результатом деления с остатком является равенство: 151 = 0512 + 151. На основе данного рассуждения этот шаг описывается следующим образом:
1514 – 05120 = 1510 – 0 + 4 = 1514.
(По существу, данный шаг пришлось делать только с целью обозначения деления на 5120.)
Наконец, делением числа 1514 на 512 определяется равенство: 1514= 2512+50. Покажем запись всей суммарной процедуры деления. При этом не учитываются цифры, вместо которых записывался знак 0 на соответствующем шаге процедуры.
3440314:
512 = 4202
–3252
1443
–1424
151
–
0
1514
–1424
50
Как было упомянуто выше, шестеричная система была выбрана потому, что число 6 не слишком большое и не слишком маленькое. Если основное число слишком большое, то и таблицы операций получаются слишком большие, следовательно, слишком большое количество основных операций необходимо знать наизусть. Если основное число слишком маленькое, то отдельные числа будут «слишком длинные». В таком случае 10, как основное число, является довольно удачным выбором.