
- •Введение.
- •Первообразная. Неопределенный интеграл, его свойства.
- •Полагая
- •2. Интегрирование подстановкой.
- •3. Интегрирования по частям. Широко применяется метод интегрирования, называемый метод интегрирования по частям.
- •Поскольку в состав интеграла уже входит произвольная постоянная, то в нее можно включить и слагаемое c и в результате получим формулу интегрирования по частям
- •4. Таблица основных формул интегрирования.
- •По теореме о дифференцировании интеграла имеем
- •Заключение.
Поскольку в состав интеграла уже входит произвольная постоянная, то в нее можно включить и слагаемое c и в результате получим формулу интегрирования по частям
![]() (11)
(11)
Эта формула представляет собой тождество, справедливое для любой пары функций u и v. В некоторых случаях (разумеется не всегда) интеграл, стоящий в (11) справа проще интеграла, стоящего слева. Тогда применение формулы имеет смысл.
Всмотримся внимательнее в формулу (11). Мы видим, что множитель u, стоящий в левом интеграле при переходе к правому интегралу заменяется на du, т.е. дифференцируется. Другой же сомножитель dv заменяется на v т.е. интегрируется.
Эта необходимость интегрирования не всего выражения, а одного сомножителя и объясняет термин дифференцирования по частям. Рассуждая абстрактно, можно утверждать, что упрощение интеграла происходит от любой из этих операций.
Однако, в подавляющем большинстве случаев, упрощение происходит именно от дифференцирования множителя u. Таким образом, если в составе подынтегральной функции есть множитель, упрощающийся от дифференцирования, то полезно применять формулу (11), приняв упомянутый множитель за u, а остальное за dv.
ПРИМЕР.
![]()
РЕШЕНИЕ.
В состав подынтегральной функции входит
lnx, производная от которого
![]() гораздо проще его самого. Поэтому
полагаем
гораздо проще его самого. Поэтому
полагаем
![]() (12)
(12)
Но ведь мы хотим воспользоваться формулой (11) и для этого нам нет необходимости привлекать все множество функций (12), а достаточно использовать одну из них. Разумеется, самое простое - взять ту функцию, которая отвечает значению C=0, т.е. положить
![]()
И в общем случае, когда применяют интегрирование по частям, то произвольную постоянную в интеграл по dv не вводят.
Имеем на основании формулы (11)
![]() (13)
(13)
Так как
![]() , (14)
, (14)
Рассмотри еще ряд примеров на применение формулы интегрирования по частям.
А)
![]() .
Полагаем
.
Полагаем
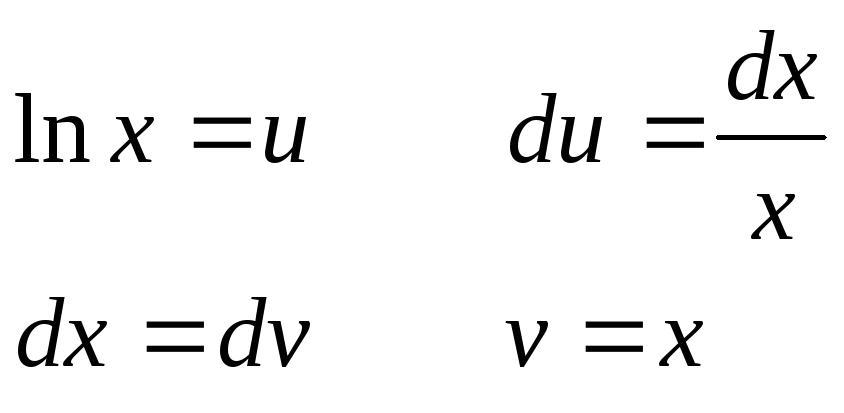
Отсюда
![]()
В)
![]() Полагаем
Полагаем
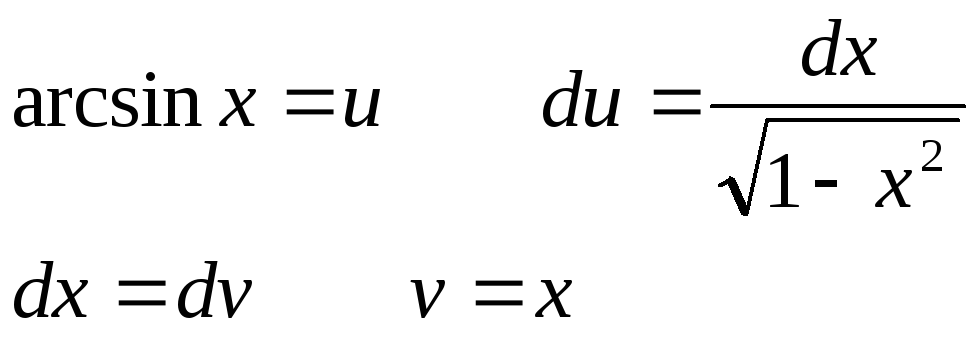
Отсюда
![]()
Но,
![]()
Значит
![]()
Во
всех рассмотренных примерах мы следовали
общему указанию: выбирать за u множитель,
упрощающийся от дифференцирования.
Попробуем отступить от этого указания.
Пусть
![]() .
.
Попробуем
за u принять множитель ex,
хотя он и не упрощается от дифференцирования.
Тогда
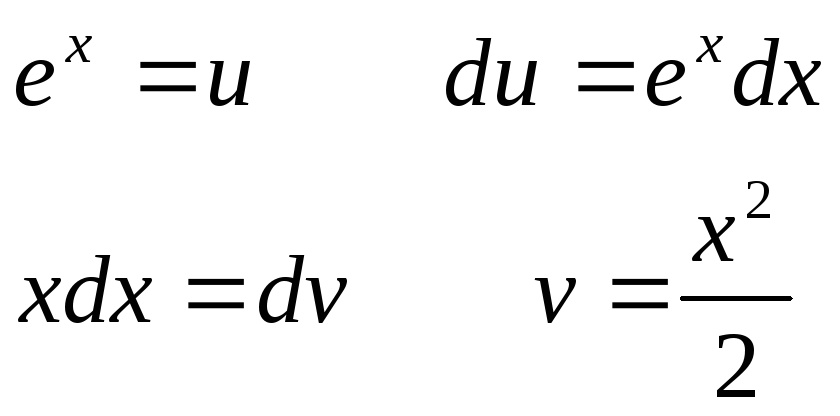
Отсюда
![]()
Хотя это равенство верное, но оно бесполезно, так как правый интеграл сложнее левого.
Однако иногда бывают ситуации, что правый интеграл в точности равен левому. Пусть, например
А)
![]() .
Тогда
.
Тогда
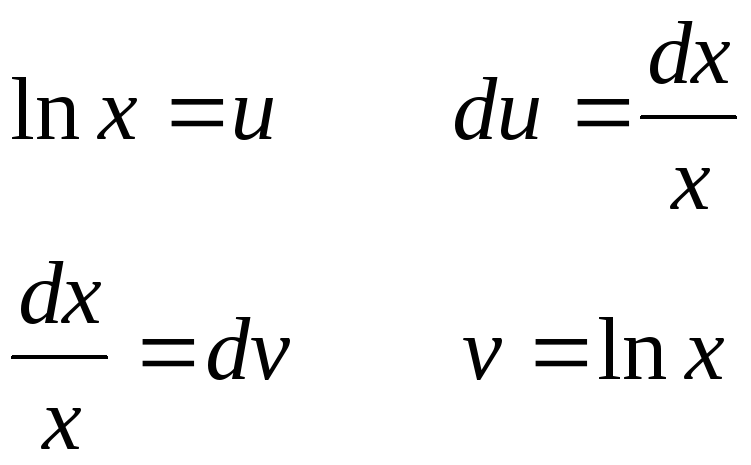
Отсюда
![]()
Справа получился исходный интеграл I. Поэтому
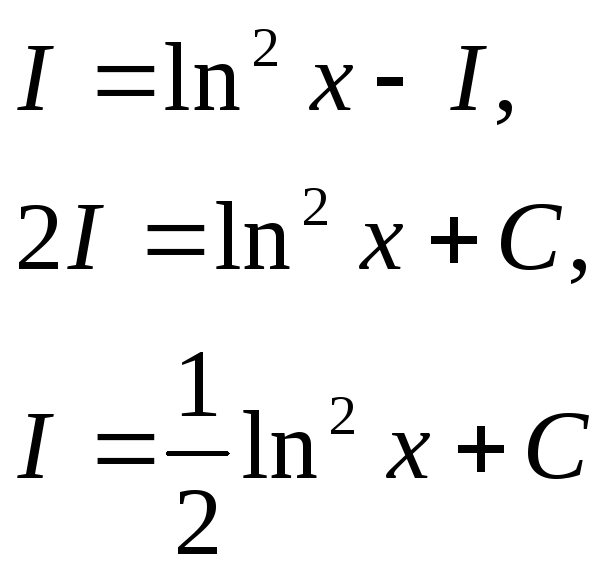
В)
![]()
Тогда
![]()
Отсюда
![]() (15)
(15)
Справа
получился интеграл примерно той же
сложности, что и исходный. Это часто
является указанием на возможность
приведения интеграла к самому себе. В
нашем случае применим интегрирование
по частям к интегралу
![]() .
.
Тогда
![]()
Отсюда
![]() (16)
(16)
Подставляя это в (15), находим
![]()
Откуда
![]() (17)
(17)
Заметим,
что нами попутно вычислен и интеграл
![]() ,
так как из (16) и (17) вытекает
,
так как из (16) и (17) вытекает
![]()
Таким образом, формула интегрирования по частям применима и когда интегралы совпадают.
то
![]() .
.
Это и есть значение исходного интеграла.
Замечание. Строго говоря, подставляя в (16), мы должны были написать не (+C), а (-C), но так как C- все равно произвольная постоянная, то безразлично какой знак перед ней ставить.
Полезно запомнить следующие 6 типов интегралов, вычислять которые удобно интегрированием по частям.
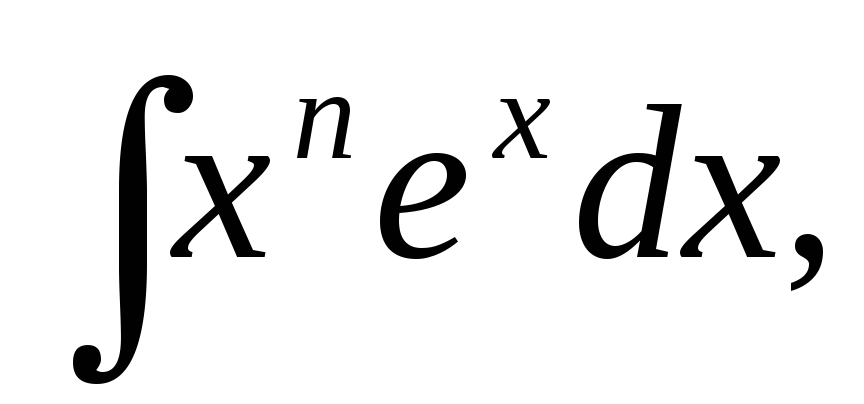 4.
4.
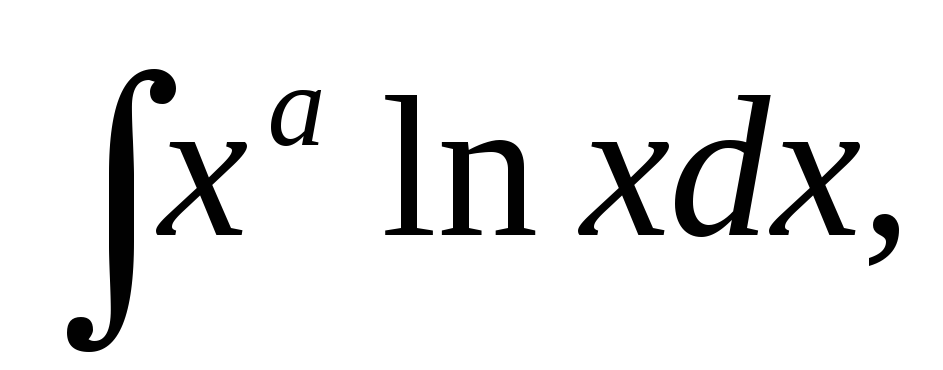
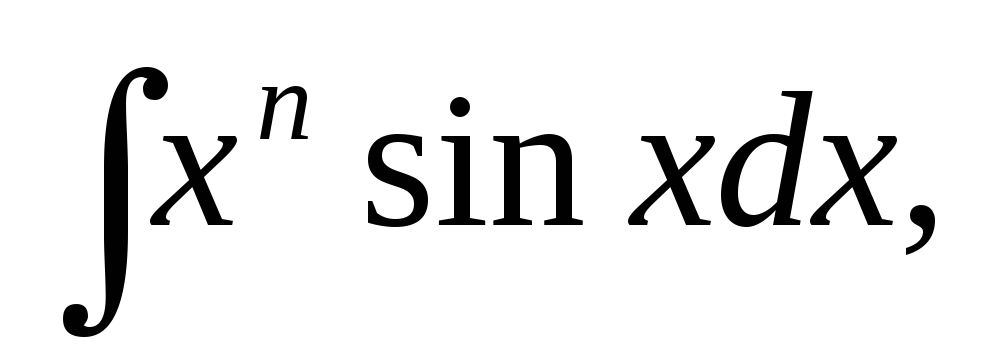 5.
5.
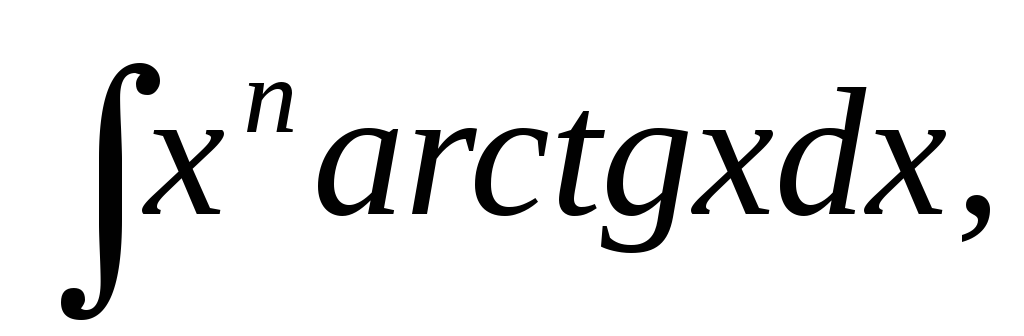
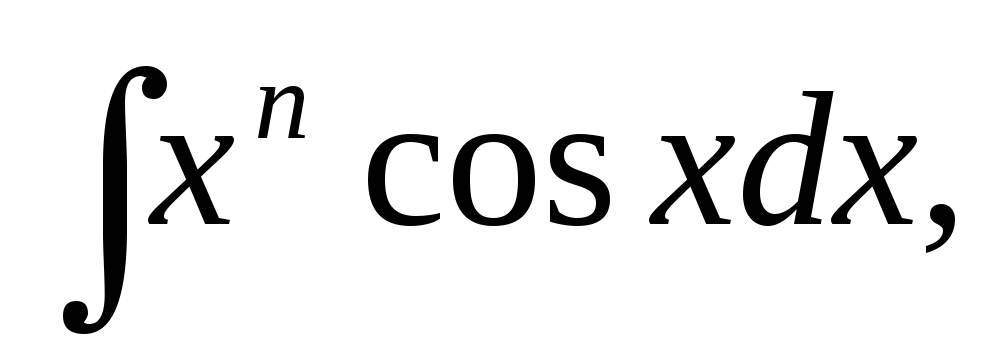 6.
6.

Для интегралов 1,2,3 следует принимать u за множитель xn. Это приведет к интегралу сходного типа, но уменьшит показатель степени на единицу. После n-кратного применения этого приема мы получим один из табличных интегралов
![]()
В интегралах 4,5,6 от дифференцирования упрощается трансцендентный множитель (т.е. lnx ,arctgx, arcsinx). Его и следует принять за u.
