
Физика 1 семестр - Колебания и волны
.pdf
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
1 |
Колебания и волны
Уравнение гармонических колебаний.
Рассмотрим пружинный маятник, т.е. груз массой m на пружине же-
сткостью k, прикрепленной к стене. Считаем, что сила тяжести и сила реакции опоры компенсируют друг друга, сила трения отсутствует.
k m
0
F
0 x
Рис. 1. Пружинный маятник.
Обозначим точку 0 – положение равновесия груза. Если груз на пружине оттянуть, деформировать пружину на величину х, то возникнет сила, возвращающая тело к положению равновесия. Проекция этой силы на ось х равна
Fx = −k x. |
(1) |
В этой формуле k – жесткость, а х – деформация пружины.
Поскольку сила упругости пружины – единственная не скомпенсированная сила, действующая на тело, можно воспользоваться вторым законом Ньютона
max (t) = −k x(t) . |
(2) |
Учитывая, что ускорение – это вторая производная от координаты по времени, получаем
|
m × x′′(t ) + k × x(t ) = 0 . |
(3) |
||
|
ω 0 ≡ |
|
, |
(4) |
Вводим обозначение |
k m |
|||

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
2 |
и получаем дифференциальное уравнение гармонических колебаний в каноническом виде:
|
x′′(t ) + ω 0 |
2× x(t) = 0 . |
(5) |
Решением этого уравнения является функция: |
|
||
|
x(t ) = A × cos(ω0 t+ ϕ0 ), |
(6) |
|
в которой А – |
амплитуда колебаний, т.е. максимальная по модулю деформа- |
||
ция пружины; |
ϕо – начальная фаза. Эти величины могут быть найдены из |
||
начальных условий: начальной координаты хo и начальной скорости |
υo. |
||
Выражение в скобках называется фазой колебаний. Она измеряется в радиа-
нах. Период колебаний пружинного маятника |
T = 2π ω0 , т.е. с учетом (4) |
||||
|
|
|
|
|
|
T = 2π |
m |
. |
(7) |
||
|
|||||
|
|
k |
|
||
Скорость – есть производная от координаты по времени, поэтому,
скорость маятника, совершающего гармонические колебания, равна |
|
υ(t) = -ω A ×sin(ω0 t+ϕ0 ). |
(8) |
Получается, что скорость маятника меняется по гармоническому закону на той же частоте ω0 . Максимальная скорость равна υm = Aω 0.
Ускорение – есть вторая производная от координаты по времени или производная от скорости по времени, поэтому, ускорение маятника, совершающего гармонические колебания, равно
a(t ) = -ω A2 ×sin(ω 0 t+ ϕ0 ). |
(9) |
Получается, что ускорение маятника меняется по гармоническому закону на той же частоте ω0 . Максимальное ускорение равно am = Aω 0 2 .

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
3 |
Физический и математический маятник.
Физическим маятником называется абсолютно твердое тело, подвешенное на горизонтальной оси, не проходящей через центр масс. Расстояние от центра масс до оси обозначим буквой b.
O |
|
N α |
OC = b |
C
α mg
Рис. 2. Физический маятник
К физическому маятнику на рис.2 приложено две силы: сила тяжести и сила взаимодействия с осью О. Момент первой из них относительно оси
подвеса равен M1 = mgb ×sinα . Момент силы N взаимодействия с осью |
|
равен нулю, поскольку сама сила направлена вдоль отрезка |
[OC ] . По вто- |
рому закону Ньютона для вращательного движения |
|
R |
|
∑ Mi = M1 = Iε , |
(10) |
где I – момент инерции маятника относительно оси О, а ε – |
угловое уско- |
рение. Отметим, момент силы тяжести стремится повернуть маятник к положению равновесия, т.е. является возвращающим. Значит, при записи этого уравнения в скалярном виде с одной стороны нужно поставить знак минус:
|
Iε = -mgb ×sin α . |
(11) |
|||||
Вспомним, что ε (t) = α′′(t) и при малых углах отклонения |
sin α = α |
||||||
|
α ′′(t ) + |
mgb |
α (t ) = 0 . |
(12) |
|||
|
|
|
|||||
|
|
I |
|
|
|
|
|
Вводим обозначение, |
ω 0 = |
|
|
(13) |
|||
mgb I |
|||||||
и окончательно имеем |
α ′′(t ) + ω0 |
2 ×α (t ) = 0. |
(14) |
||||
Мы получили уравнение (5), но не для смещения, а для угла поворота. От того, как обозначена искомая функция x(t) или α (t ) , разумеется, ничего не зависит. Решение уравнения (14) будет таким же, как и для уравнения (5)

Конспект лекций по Физике для студенческих групп Z3111, Z3221, Z3442k, Z3532k 4
α (t) = A × cos(ω0 t+ ϕ 0). |
(15) |
Физический маятник при малых углах отклонения совершает гармонические колебания с периодом T = 2π ω0 , т.е. с учетом (13)
ω0 , т.е. с учетом (13)
T = 2π |
I |
(16) |
. |
mgb
Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити. Его можно рассматривать, как
α
L
Рис. 3. Математический маятник
частный случай физического маятника с b = L и моментом инерции I = mL2 .
Сказанное обозначает, что математический маятник при малых углах отклонения совершает гармонические колебания с периодом
T = 2π |
mL2 |
= 2π |
L |
. |
(17) |
mgL |
|
||||
|
|
g |
|
||
Затухающие колебания.
Рассмотрим пружинный маятник, погруженный в вязкую среду. Считаем, что сила тяжести, сила Архимеда и сила реакции опоры компенсируют друг друга. Сухое трение тела о поверхность отсутствует.
k |
m |
Fc |
|
|
Fx |
0 x
Рис. 4. Пружинный маятник в вязкой среде.

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
5 |
На груз действует сила упругости пружины, возвращающая тело к положению равновесия. Проекция этой силы на ось х равна
Fx = −k x. |
(18) |
Кроме силы упругости пружины на тело действует сила сопротивления среды или сила вязкого трения, которая направлена в сторону, противоположную направлению скорости. Величина этой силы равна
|
|
Fc |
= cυ. |
|
|
|
(19) |
|
|
|
|
R |
|
||
По второму закону Ньютона |
ma = F + Fc . Учитывая, что |
||||||
′′ |
′ |
с учетом направления сил получаем |
|||||
a(t) = x (t), |
а υ(t) = x (t), |
||||||
|
|
mx′′(t) + cx′(t) + k x(t ) = 0 . |
(20) |
||||
|
β ≡ c 2m ; |
ω 0 ≡ |
|
|
|
|
|
Вводим обозначения |
|
k m |
и получаем дифферен- |
||||
циальное уравнение затухающих колебаний в каноническом виде |
|||||||
|
|
x¢¢(t) + 2β × x¢(t) + ω0 |
2 ×x(t) = 0 . |
(21) |
|||
Сразу отметим, что затухающие колебания не являются гармониче-
скими. Решением уравнения (21) будет функция
x(t) = A ×e− β t × cos(ω t + ϕ |
). |
(22) |
|
0 |
0 |
|
|
В этом уравнении ϕ 0 – начальная фаза колебаний. Частота затухающих ко-
лебаний ω меньше частоты собственных колебаний |
ω 0 |
|||
ω = |
|
|
, |
|
ω 0 |
2 - β 2 |
(23) |
||
Соответственно период затухающих колебаний будет больше периода незатухающих гармонических колебаний.
Произведение, стоящее перед косинусом, есть убывающая со временем амплитуда колебаний:
A(t) = A ×e− β t . |
(24) |
0 |
|
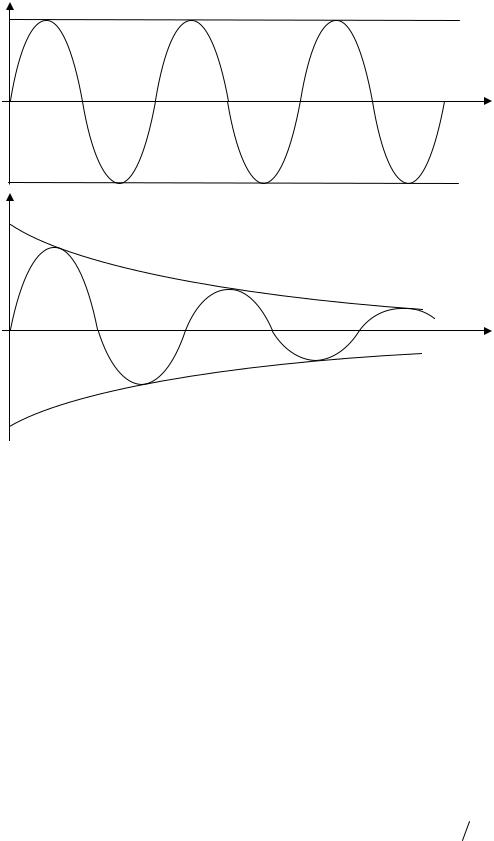
Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
6 |
x
A
t
–A
x
Ao
A = A0 ×e− β t
t
–A o
Рис. 5. Незатухающие и затухающие колебания.
Рассмотрим функцию (24), найдем отношение двух следующих друг за другом амплитуд колебаний. Натуральный логарифм такого отношения называется логарифмическим декрементом затухания θ
θ = ln |
AN |
. |
(25) |
|
|||
|
AN +1 |
|
|
Найдем, чему равен логарифмический декремент для двух амплитуд, взятых в моменты времени t и t+T .
θ = ln |
A0×e− βt |
= ln |
e− βt |
|
= ln |
1 |
= ln eβT |
= βT. |
(26) |
|
A0×e− β (t+T ) |
e− βt e− βT |
e− βT |
||||||||
|
|
|
|
|
|
|||||
Величина, обратная логарифмическому декременту, равна числу N |
коле- |
|||||||||
баний, за время которых амплитуда уменьшится в |
е раз |
N = 1 θ . |
||||||||
Добротностью Q колебательной системы называется величина |
||||||||||
|
|
|
Q = π |
= π N. |
|
|
|
(27) |
||
|
|
|
θ |
|
|
|
|
|
|
|

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
7 |
Можно сказать, что добротность – это количество колебаний, которое совершит маятник до остановки.
Вынужденные колебания. Резонанс.
Рассмотрим пружинный маятник, погруженный в вязкую среду. Считаем, что сила тяжести, сила Архимеда и сила реакции опоры компенсируют друг друга. Сухое трение тела о поверхность отсутствует.
k |
Fc f |
 Fx m
Fx m
0 x
Рис. 6. Пружинный маятник под действием внешних сил.
На груз действует сила упругости пружины, возвращающая тело к положению равновесия. Проекция этой силы на ось х равна
Fx = -k x. |
(28) |
Кроме силы упругости пружины на тело действует сила сопротивления среды или сила вязкого трения, которая направлена в сторону, противоположную направлению скорости. Величина этой силы равна
Fc = cυ. |
(29) |
Кроме этих двух сил, на тело действует еще внешняя периодическая (в рассматриваемом случае гармоническая) сила
f = f0 ×cosω t. |
(30) |
Применим второй закон Ньютона ко всем силам, приложенным к маятнику. Полученное выражение спроектируем на ось ox:
|
ma = -kx - cυ + f0 ×cosωt. |
(31) |
′′ |
′ |
|
Учтем, что a(t) = x (t), |
а υ(t) = x (t), перепишем получившееся уравнение |
|
m × x′′(t ) + c × x′(t ) + k × x(t) = f0 ×cosω t. |
(32) |
|

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, |
Z3442k, Z3532k |
8 |
|||
|
β º c 2m ; |
ω 0 º |
|
; |
|
|
Вводим обозначения |
k m |
и получаем |
||||
дифференциальное уравнение вынужденных колебаний в каноническом виде
x¢¢(t ) + 2β × x¢(t ) + ω02 ×x(t ) = ( f0  m ) × cosω t. (33)
m ) × cosω t. (33)
Решением этого уравнения будет гармоническая функция на частоте вынуждающей силы ω
x(t ) = A × cos(ω t+ ϕ0 ). |
(34) |
Амплитуда и начальная фаза в этом уравнении являются функциями частоты
A = |
|
|
f0 |
m |
|
|
|
; |
(35) |
|
|
|
|
|
|
|
|||
(ω 0 |
2 − ω 2 )2 + 4β 2ω 2 |
||||||||
ϕ 0 |
= −arctg |
|
2βω |
|
|
|
|||
|
|
. |
|
|
(36) |
||||
ω |
2 − ω 2 |
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
А
1 |
β1 < β2 < β3 |
2
3
ωо ω
ϕо
0
-π/2
- π
ω
3
2
1
Рис. 7. Резонансные кривые
Функция А(ω) имеет максимум при частотах, близких к ωо. Чем меньше коэффициент затухания β, тем острее выражен пик на зависимости.

Конспект лекций по Физике для студенческих групп |
Z3111, Z3221, Z3442k, Z3532k |
9 |
Явление возрастания амплитуды колебаний при частотах, близких к частоте собственных колебаний называется резонансом.
Анализ формулы (35) дает
ω |
p |
= |
ω 2 |
− 2β 2 |
, |
(37) |
|
|
0 |
|
|
|
Что немного меньше и частоты собственных колебаний ωо, и частоты затухающих колебаний (23). Амплитуда колебаний на этой частоте равна
Ap = |
|
f0 |
m |
|
||||
|
|
|
|
|
|
. |
(38) |
|
|
|
|
|
|
|
|||
2β |
ω |
|
||||||
|
2 − β 2 |
|
||||||
|
|
|
|
0 |
|
|
|
|
Из двух последних формул следует, что в отсутствие трения амплитуда колебаний при резонансе стремилась бы к бесконечности, а частота резонанса равнялась бы ωо.
Из формулы (36) и графика соответствующей функции видно, что колебания маятника отстают по фазе от вынуждающей силы. На малых частотах колебания происходят практически в одинаковой фазе, а на больших частотах – в противофазе.
Энергия гармонических колебаний.
Потенциальная энергия сжатой пружины равна
|
|
|
E |
|
= |
1 |
kx2 |
= |
1 |
kA2 cos2 (ω |
t + ϕ |
|
). |
|
|
|
(39) |
||||||
|
|
|
|
|
|
0 |
|
|
|
||||||||||||||
|
|
|
Π |
2 |
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Кинетическая энергия движущегося маятника равна |
|
|
|
|
|
||||||||||||||||||
E = |
1 |
mυ 2 |
= |
1 |
mυ |
|
2 sin2 |
(ω |
t + ϕ |
|
) = |
1 |
mω 2 A2 sin2 |
(ω |
t + ϕ |
|
). |
||||||
|
|
|
0 |
|
0 |
||||||||||||||||||
Κ |
2 |
|
|
2 |
|
|
m |
|
0 |
|
2 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вспомним, что жесткость пружины, масса груза и частота собственных коле-
баний связаны соотношением (4) ω 0 ≡ 
 k
k m , и закончим выкладки для кинетической энергии:
m , и закончим выкладки для кинетической энергии:
E |
= |
1 |
kA2 sin2 (ω |
t + ϕ |
|
). |
(40) |
|
0 |
||||||
Κ |
2 |
0 |
|
|
|
||
|
|
|
|
|
|
||
Полная механическая энергия маятника равна сумме потенциальной и кинетической; сложим их и получим

Конспект лекций по Физике |
для студенческих групп |
Z3111, Z3221, Z3442k, |
Z3532k |
10 |
||||||
E = |
1 |
kA2 cos2 (ω0t + ϕ0 ) + |
1 |
kA2 sin2 (ω0t + ϕ0 ) = |
1 |
kA2 . |
(41) |
|||
|
|
|
||||||||
2 |
|
2 |
|
2 |
|
|
|
|||
Получилось, что полная энергия – величина постоянная, чего и следовало ожидать.
Найдем средние значения потенциальной и кинетической энергий. При этом учтем, что средние значения квадрата косинуса и квадрата синуса одинаковы и равны ½.
E |
= |
1 |
kA2 |
sin2 (ω |
t + ϕ |
|
) |
= |
1 |
kA2 , |
(42) |
||||||
|
|
0 |
|
|
|||||||||||||
Κ |
2 |
|
|
0 |
|
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E |
= |
1 |
kA2 |
cos2 (ω |
t + ϕ |
|
) |
= |
1 |
kA2 . |
(43) |
||||||
|
0 |
|
|||||||||||||||
Π |
2 |
|
|
0 |
|
|
|
4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Средние значения кинетической и потенциальной энергии равны друг другу.
Волны. Основные определения.
Волна – это процесс распространения колебаний в пространстве.
Источник, колеблющийся на частоте ω, заставляет точки окружающей среды колебаться на той же частоте, но с некоторой задержкой по фазе. Чем больше расстояние от источника, тем больше разность фаз. Отметим, что в волновом процессе частицы среды не перемещаются, а колеблются около своих положений равновесия.
В случае, когда колебания точек происходит в направлении вектора скорости волны, волна называется продольной. Если же колебания происходят в направлении, перпендикулярном направлению вектора скорости, то волна называется поперечной.
Геометрическое место точек, до которых доходят колебания к данному моменту времени называется волновым фронтом. Волновой фронт делит пространство на две области: вовлеченную в волновой процесс и не вовлеченную.
Геометрическое место точек среды, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности неподвижны, а волновой фронт бежит со скоростью волны. В каждый момент времени волновой фронт совпадает с одной из волновых поверхностей.
Волновые поверхности могут быть самой разнообразной формы. В простейших случаях это сфера, плоскость, цилиндр. Соответствующие волны
