1. Моделирование случайных величин и векторов и определение их статистических характеристик

Цель работы: изучение элементов теории вероятностей, используемых при постановке и решении задач оценивания.

1. Основные теоретические сведения

В прикладных задачах, связанных со статистическими методами обработки информации, весьма важным является, с одной стороны, умение получать (моделировать) реализации случайных величин, распределенных по тому или иному закону, а с другой – умение определять свойства случайных величин по их реализациям [1,2].

Компьютерные программы, предназначенные для моделирования случайных величин, называют датчиками случайных чисел. Несмотря на свое предназначение, такие программы производят вычисления по вполне определенному алгоритму, так что получаемая реализация, как правило, зависит лишь от начальных условий алгоритма. Поэтому формируемые датчиками числовые последовательности называют псевдослучайными.

В большинстве случаев датчики вырабатывают реализации независимых между собой одинаково распределенных случайных величин с заданной плотностью распределения вероятностей. Для получения случайной величины, имеющей то или иное распределение, обычно сначала получают случайную величину с достаточно простой плотностью распределения (например, равномерной), а затем подвергают ее такому преобразованию, которое обеспечивает получение заданной плотности распределения вероятностей. Обычно моделировать приходится гауссовские случайные величины. Как правило, датчик генерирует стандартизованные случайные величины, т.е. центрированные, с единичным среднеквадратическим отклонением (СКО). Для получения случайной величины x с заданными значениями математического ожиданияx и СКО σ стандартизированные случайные величины x_ст подвергают преобразованию

x =x + σ x_ст.

В задачах обработки навигационной информации нередко приходится иметь дело с двумерными гауссовскими векторами. Так, при решении навигационных задач на плоскости нередко полагают, что координаты объекта представляют собой двумерный гауссовский вектор с математическим ожиданием в точке его предполагаемого местонахождения. Гауссовским случайным вектором x называется такой, для которого функция плотности распределения вероятностей определяется в виде [2]

, (1)

где n – размерность вектора, P – матрица ковариаций. Для двумерного центрированного вектора выражение (1) можно преобразовать к виду

. (2)

Здесь

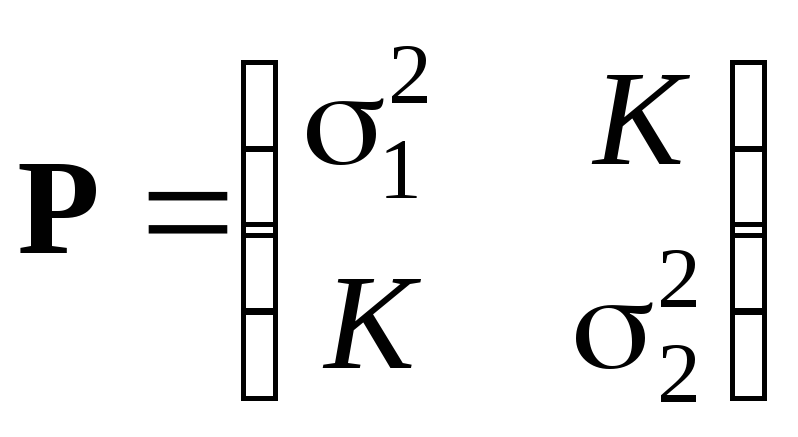, (3)

где σ_1,2 – СКО составляющих двумерного вектора; K – коэффициент корреляции составляющих; – нормированный коэффициент корреляции.

Пример графика функции приведен на рис. 1. Поскольку получаемая трехмерная картина не очень удобна для восприятия, обычно рассматривают горизонтальные сечения функции плотности распределения, называемые изолиниями. Для плотности (2) изолинии представляют собой эллипсы равных вероятностей. Поскольку изолинии могут соответствовать разным уровням плотности распределения, размеры полуосей таких эллипсов также будут отличаться. Среди эллипсов равных вероятностей выделяют так называемый среднеквадратический эллипс ошибок, пересекающий осиx₁ и x₂ в точках, совпадающих со значениями соответствующих СКО.

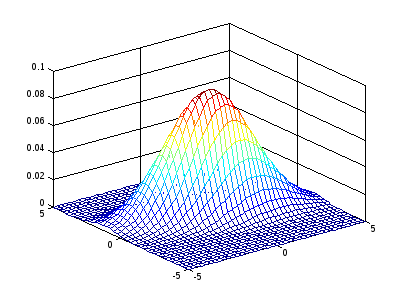
Рис. 1. Плотность распределения вероятностей двумерного гауссовского вектора

Параметры среднеквадратического эллипса ошибок могут быть найдены по следующим формулам:

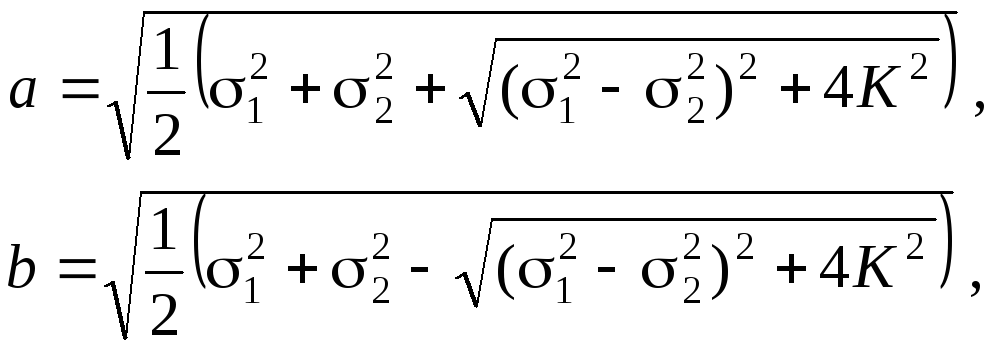
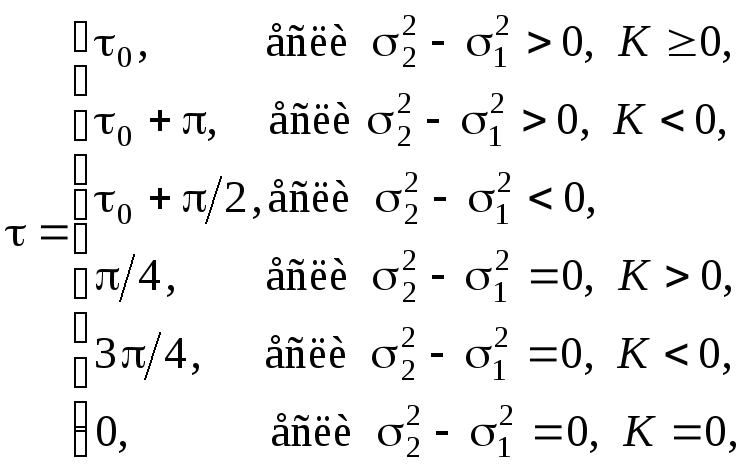
где .

Здесь a, b – соответственно большая и малая полуоси эллипса,  – дирекционный угол (рис. 2).

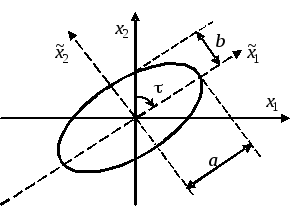
Рис. 2. Среднеквадратический эллипс ошибок

При обработке навигационной информации часто возникает задача определения статистических свойств проекции случайного вектора на заданное направление *. Например, при движении судна вдоль фарватера наиболее важной представляется величина ошибки определения координат места в направлении поперек фарватера. Полагая, что ошибка определения координат судна на плоскости описывается как двумерный случайный вектор, величина ошибки вдоль фарватера может быть найдена в результате решения задачи, которая формулируется следующим образом. Задан двумерный случайный вектор x = (x₁  x₂)^Т с математическим ожиданием x = (x₁x₂)^Т и матрицей ковариаций (3). Требуется найти математическое ожидание  и дисперсию скалярной случайной величины  = x₁sin* + x₂cos*. Искомые параметры могут быть получены из соотношений [2]

 = x₁sin* +x₂cos*;

.

Рассмотрим далее вопрос моделирования реализаций случайного вектора. В том случае, когда компоненты вектора между собой независимы, т.е. матрица ковариаций диагональная, для получения реализации вектора достаточно промоделировать отдельно каждую компоненту в соответствии с заданными свойствами. Если матрица ковариаций недиагональная, задача может быть решена с помощью ортогонального преобразования вектора с некоррелированными компонентами. К примеру, если требуется получить реализации двумерного центрированного гауссовского вектора x с недиагональной матрицей ковариаций вида (3), то сначала формируется набор реализаций центрированного гауссовского вектора с матрицей ковариаций, а реализации искомого вектора получают путем преобразования, где.

При проверке свойств случайных величин по их реализациям наиболее часто вычисляют так называемые выборочные математическое ожидание и дисперсию. Несмещенные оценкиимогут быть получены из соотношений

, (4)

, (5)

, (6)

где x^(j) – независимые между собой реализации случайной величины, L – объем выборки, причем формула (5) используется в том случае, когда математическое ожидание случайной величины известно, а формула (6) – когда оно является выборочным и определяется из соотношения (4).

Иногда интерес представляет оценка медианы распределения x_1/2, определяемой из соотношения

.

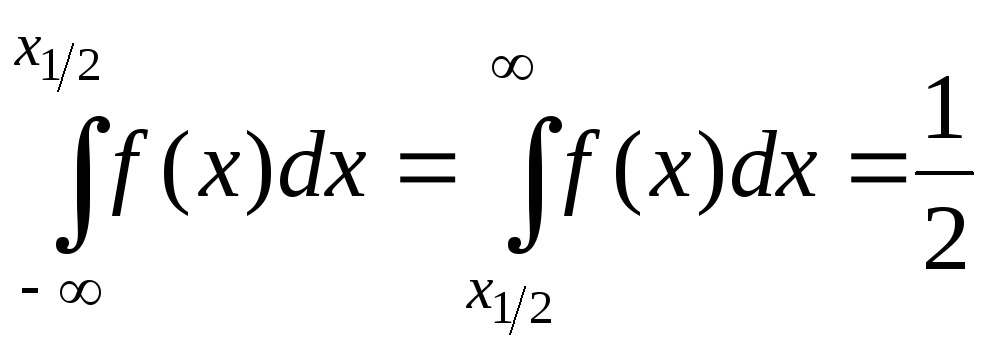Для симметричных распределений (в частности, равномерного и гауссовского), медиана совпадает с математическим ожиданием.

Для нахождения выборочной медианы используют следующий алгоритм. Значения x^(j) располагают в порядке возрастания (или убывания), получая так называемый вариационный ряд ,. Тогда еслиL нечетно, выборочная медиана равна среднему элементу вариационного ряда, а если четно – полусумме средних элементов:

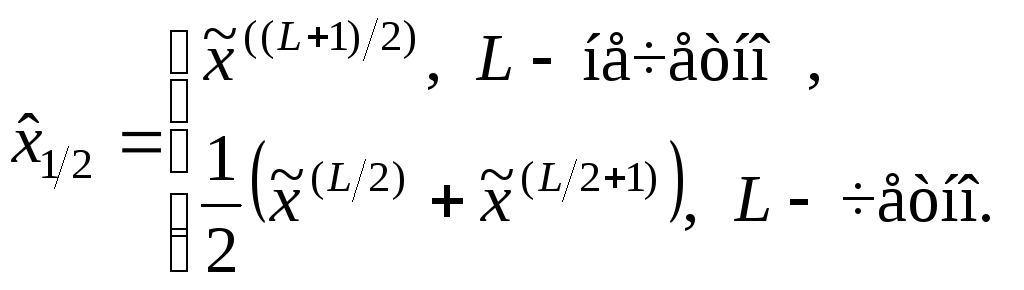
Располагая набором независимых между собой реализаций x^(j), можно не только вычислить выборочные характеристики, но и оценить саму функцию плотности распределения вероятности, которая в наиболее полном объеме характеризует свойства случайной величины. В качестве такой оценки выступает гистограмма, представляющая собой ступенчатую фигуру в виде сдвинутых друг к другу прямоугольников. Основаниями прямоугольников служат отрезки оси абсцисс, длины которых равны заданным длинам интервалов, а высотами - отрезки, длины которых равны количеству реализаций, относящихся к данному интервалу.