
- •Кафедра медицинской и биологической физики
- •Рекомендации к работе с пособием.
- •Приведём пример оформления решения задачи.
- •1. Биомеханика
- •1.3. Определите напряжение при сжатии дентина зуба до относительной деформации 0,01, если считать дентин зуба упругим материалом с модулем Юнга равным 18600 мПа.
- •1.4. Подсчитайте относительное изменение объема в процентах при растяжении на 4 % образца сплава золота. Коэффициент Пуассона для сплава примите равным 0,42.
- •1.11. Определите модуль сдвига для стали, если модуль Юнга для нее равен 198,00 гПа, а коэффициент Пуассона равен 0,31.
- •1.18. На рисунке представлены зависимости предела хрупкой прочности - линия “а” и предела текучести - линия “б” от абсолютной температуры для литьевого зуботехнического сплава.
- •2. Реология и гемодинамика
- •2.29. Для описания кинетики деформации растяжения мембраны эритроцитов, Ренд и Бертон предложили линейную реологическую модель:
- •2.30. При механическом воздействии на биологические ткани они проявляют временные эффекты:
- •1.7. Силу реакции Naопределим рассмотрев одно из двух условий равновесия балки – условие равенства нулю суммы моментов всех приложенных к заготовке сил.
- •1.11. Связь модуля сдвига (g), модуля Юнга (e) и коэффициента Пуассона (μ) определяется формулой:.
- •1.12. Связь модуля сдвига (g), модуля Юнга (e) и коэффициента Пуассона (μ) определяется формулой:.
- •1.22. Ответ очевиден из графика – напряжение при разрушении было 2,4 мПа.
- •1.23. По Гриффитсу хрупкое разрушение кристаллического материала сопровождается образованием двух новых поверхностей, которые до того не существовали.
- •1.24. По Гриффитсу хрупкое разрушение кристаллического материала сопровождается образованием двух новых поверхностей, которые до того не существовали.
- •1.27. Полная энергия кубика:
- •1.28. Полная энергия кубика:
- •1.29. Полная энергия кубика:
- •2.10. Отобразим на рисунке модели последовательно соединённых элементов Гука. Последовательное соединение означает соединение конца первого элемента со вторым.
- •2.30. Ответ: г. Релаксацию напряжения, ползучесть, механический гистерезис, сдвиг фаз между периодически задаваемым напряжением и получающейся при этом деформацией.
- •2.32. По современным представлениям, плазма крови относится к ньютоновским жидкостям.
- •2.57. Рассмотрим силы, действующие на шарик при таком движении. Сформулируем динамические условия равномерного движения шарика.
- •Справочные материалы Фундаментальные постоянные
- •Наименования и обозначения приставок си для образования десятичных кратных и дольных единиц и их множители
- •Правила приближённых вычислений.
2.30. Ответ: г. Релаксацию напряжения, ползучесть, механический гистерезис, сдвиг фаз между периодически задаваемым напряжением и получающейся при этом деформацией.
2.31.
При постоянной температуре («в
физиологическом диапазоне») и постоянной
скорости сдвига кажущаяся вязкость
крови определяется формулой:
![]() где α - коэффициент, зависящий от
белкового состава плазмы крови ηа
- кажущаяся вязкость крови при заданном
гематокрите, η0
-вязкость
плазмы, H - гематокрит.
где α - коэффициент, зависящий от
белкового состава плазмы крови ηа
- кажущаяся вязкость крови при заданном
гематокрите, η0
-вязкость
плазмы, H - гематокрит.
Формула
для случая с известным по условию задачи
гематокритом Н1:
![]()
Из
полученной формулы получим выражение
коэффициента α, имея в виду неизменный
состав плазмы:
![]() .
.
Используем
α с тем, чтобы получить формулу для
кажущейся вязкости крови при гематокрите
Н2:
![]()
Подставим
в получившееся выражение числовые
данные и получим окончательный результат:
![]()
2.32. По современным представлениям, плазма крови относится к ньютоновским жидкостям.
Вязкость
ньютоновской жидкости зависит от
природы жидкости и от температуры и не
зависит от скорости сдвига. Реологическое
уравнение для ньютоновской жидкости:
![]() где
где![]() напряжение
сдвига,
напряжение
сдвига,![]() вязкость,
а
вязкость,
а![]() скорость
сдвига. Получим расчётную формулу для
скорости сдвига. Подставим в получившееся
выражение числовые данные и получим
окончательный результат.
скорость
сдвига. Получим расчётную формулу для
скорости сдвига. Подставим в получившееся
выражение числовые данные и получим
окончательный результат.
Ответ:
![]()
![]()
2.33.
Математическое выражение, характеризующее
реологическое поведение крови в рамках
модели Кессона:
![]() где
τ - напряжение сдвига, τ0
- предел текучести, k - кессоновская
вязкость,
где
τ - напряжение сдвига, τ0
- предел текучести, k - кессоновская
вязкость,
![]() скорость
сдвига.
скорость
сдвига.
Асимптотическая
вязкость
![]() - соответствует ньютоновской (кажущейся)
вязкости крови при больших скоростях
сдвига
- соответствует ньютоновской (кажущейся)
вязкости крови при больших скоростях
сдвига
Выражение
для ньютоновской (кажущейся) вязкости
жидкости, реологическое поведение
которой описывается моделью Кессона: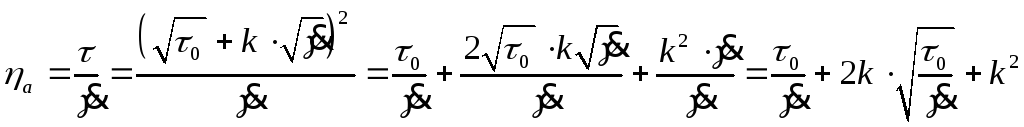
Отсюда
легко устанавливается связь между
асимптотической вязкостью и кессоновской
вязкостью:
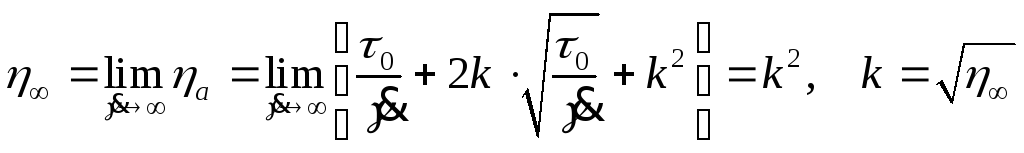
Получим расчётную формулу для напряжения сдвига. Подставим в получившееся выражение числовые данные, чтобы получить окончательный результат:
![]() мПа.
мПа.
2.34.
В математическое выражение, описывающую
модель Кессона - ![]() дважды подставим данные из условия
задачи и получим систему уравнений.
Решив систему, найдём кессоновскую
вязкость k.
дважды подставим данные из условия
задачи и получим систему уравнений.
Решив систему, найдём кессоновскую
вязкость k.
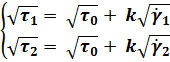 ,
,
![]() .
.
Ответ:
![]() =
=![]()
![]() .
.
2.35.
В математическое выражение, описывающую
модель Кессона - ![]() дважды подставим данные из условия
задачи и получим систему уравнений.
Решив систему, найдём
дважды подставим данные из условия
задачи и получим систему уравнений.
Решив систему, найдём ![]() .
.
 ,
,
![]() .
.
Ответ:
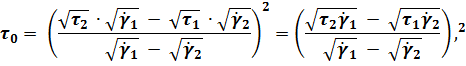
![]() ,
,
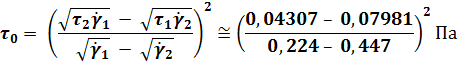
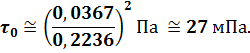
2.36.
В задаче 2.32 было показано, что
асимптотическая вязкость ![]() равна квадрату кессоновской вязкости
равна квадрату кессоновской вязкости
![]() .
Для получения кессоновской вязкости
в математическое выражение, описывающую
модель Кессона -
.
Для получения кессоновской вязкости
в математическое выражение, описывающую
модель Кессона - ![]() ,
дважды подставим данные из условия
задачи и получим систему уравнений.
,
дважды подставим данные из условия
задачи и получим систему уравнений.
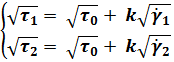 ,
,
![]() .
.
Ответ:

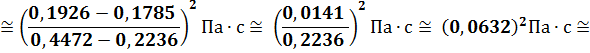
![]() .
.
2.37.
По определению кажущаяся вязкость
![]() (иное название –«ньютоновская вязкость
неньютоновской жидкости») есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ.
(иное название –«ньютоновская вязкость
неньютоновской жидкости») есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ. ![]() .
.
2.38.
По определению кажущаяся вязкость
![]() (иное название –«ньютоновская вязкость
неньютоновской жидкости») есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ.
(иное название –«ньютоновская вязкость
неньютоновской жидкости») есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ.![]() .
.
2.39.
По определению кажущаяся вязкость
![]() (иное название –«ньютоновская вязкость
неньютоновской жидкости»)есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ.
(иное название –«ньютоновская вязкость
неньютоновской жидкости»)есть частное
от деления напряжения сдвига на
полученную при этом скорость сдвига.
Ответ.![]() ,
,
![]() =
=![]() .
.
2.40.
Если предположить, что в рассматриваемом
случае депонирования крови не происходит
и саму кровь можно рассматривать как
несжимаемую жидкость, то окажется
справедливым следствие закона сохранения
массы – уравнение неразрывности: ![]() ,
где
,
где ![]() - объёмная скорость,
- объёмная скорость, ![]() и
и ![]() - суммарные поперечные сечения сосудистого
русла в двух участках, отличающихся
калибром сосудов кровеносной
системы.
- суммарные поперечные сечения сосудистого
русла в двух участках, отличающихся
калибром сосудов кровеносной
системы.![]() и
и![]() - линейные скорости кровотока в
рассматриваемых участках. Итак, объёмная
скорость постоянна по всему сосудистому
руслу
- линейные скорости кровотока в
рассматриваемых участках. Итак, объёмная
скорость постоянна по всему сосудистому
руслу ![]() .
Ответ: отношение равно единице
.
Ответ: отношение равно единице ![]() .
.
2.41.
Если предположить, что в рассматриваемом
случае депонирования крови не происходит
и саму кровь можно рассматривать как
несжимаемую жидкость, то окажется
справедливым следствие закона сохранения
массы – уравнение неразрывности: ![]() ,
где
,
где ![]() - объёмная скорость,
- объёмная скорость, ![]() и
и ![]() - суммарные поперечные сечения сосудистого
русла в двух участках, отличающихся
калибром сосудов кровеносной
системы.
- суммарные поперечные сечения сосудистого
русла в двух участках, отличающихся
калибром сосудов кровеносной
системы.![]() и
и![]() - линейные скорости кровотока в
рассматриваемых участках. Откуда
следует:
- линейные скорости кровотока в
рассматриваемых участках. Откуда
следует:![]() Ответ:
Ответ: ![]() .
.
2.42.
Оценку времениt
можно сделать, если предположить, что
в рассматриваемом случае депонирования
крови не происходит и саму кровь можно
рассматривать как несжимаемую жидкость,
то окажется справедливым следствие
закона сохранения массы – уравнение
неразрывности: ![]() ,
где
,
где ![]() - объёмная скорость,
- объёмная скорость, ![]() и
и ![]() - суммарные поперечные сечения аорты
и капиллярного русла.
- суммарные поперечные сечения аорты
и капиллярного русла.![]() и
и![]() - линейные скорости кровотока в аорте
и капилляре. Проведённые рассуждения
позволяют найти линейную скорость в
капилляре:
- линейные скорости кровотока в аорте
и капилляре. Проведённые рассуждения
позволяют найти линейную скорость в
капилляре:
![]() .
.
![]() .
.
Ответ:
![]() .
.
2.43.
Если предположить, что в рассматриваемом
случае депонирования крови не происходит
и саму кровь можно рассматривать как
несжимаемую жидкость, то окажется
справедливым следствие закона сохранения
массы – уравнение неразрывности: ![]() ,
где
,
где ![]() - объёмная скорость,
- объёмная скорость, ![]() и
и ![]() - суммарные поперечные сечения аорты
и сосудистого русла.
- суммарные поперечные сечения аорты
и сосудистого русла. ![]() и
и ![]() - линейные скорости кровотока в
рассматриваемых участках. Откуда
следует:
- линейные скорости кровотока в
рассматриваемых участках. Откуда
следует: ![]() .
.
Ответ:
![]() 0,06
0,06 ![]() .
.
2.44.
Для случая течения по гладкостенной
трубке число Рейнольдса:![]() .
Подставим данные из условия задачи в
расчётную формулу для числа Рейнольдса
и получим ответ:
.
Подставим данные из условия задачи в
расчётную формулу для числа Рейнольдса
и получим ответ:
![]() .
.
2.45.
Вязкие жидкости и газы могут иметь
два режима течения: ламинарный и
турбулентный. Чтобы определить режим
течения необходимо воспользоваться
одним из безразмерных параметров. Для
случая течения по гладкостенной трубке
подходящим параметром является число
Рейнольдса - Re.
Формулы для числа Рейнольдса:
![]() режим ламинарный,
режим ламинарный,![]() режим турбулентный. Подставим данные
из условия задачи в расчётную формулу
для числа Рейнольдса. Сравним со
значением критического числа полученный
результат. Сделаем окончательный вывод
о режиме течения:
режим турбулентный. Подставим данные
из условия задачи в расчётную формулу
для числа Рейнольдса. Сравним со
значением критического числа полученный
результат. Сделаем окончательный вывод
о режиме течения:
![]()
![]() Режим
- турбулентный.
Режим
- турбулентный.
2.46.
При ламинарном течении ньютоновской
жидкости по цилиндрической трубке
линейная скорость изменяется с
расстоянием от оси трубки по параболическому
закону: ![]() .
Максимальная линейная скорость жидкости
будет на оси трубки:
.
Максимальная линейная скорость жидкости
будет на оси трубки:
![]() .
Из формулы найдём искомую разность
давлений:
.
Из формулы найдём искомую разность
давлений: ![]() .
Подставим данные из условия задачи в
расчётную формулу. Получим ответ:
.
Подставим данные из условия задачи в
расчётную формулу. Получим ответ:
![]() .
.
2.47. Проанализируем условия стационарного течения по трубке: при стационарном течении вязкой жидкости по трубке объёмная скорость течения (расход) жидкости постоянен во времени. Отсюда следует, что слой жидкости, находящийся на некотором расстоянии от оси трубки должен двигаться с определённой неизменной во времени скоростью, т.е. в трубке должно наблюдаться «телескопическое» течение. Каждый из коаксиальных цилиндрических слоёв должен иметь постоянную скорость.
Истолкуем полученный результат с позиций законов динамики: с точки зрения законов динамики описанная ситуация возможна только в случае скомпенсированного действия сил на каждый из тонких коаксиальных слоёв. Проиллюстрируем сказанное рисунком.

V = const, FТ = FД
Запишем
равенство сил, используя понятие
напряжение сдвига, реологический закон
Ньютона и приняв во внимание, что
градиент скорости направлен от стенки
трубки к оси: для приосевого цилиндра
радиуса r
FД
=![]() ,FТ
=
,FТ
=
![]() ,
откуда
,
откуда
![]() для любой вязкой жидкости.Подставим
данные из условия задачи в расчётную
формулу. Получим ответ:
для любой вязкой жидкости.Подставим
данные из условия задачи в расчётную
формулу. Получим ответ:
![]() .
.
2.48.
Вспомним формулу Пуазейля для
течения ньютоновской жидкости по
цилиндрической трубке и условия, при
которых она была выведена: ![]() при
пуазейлевом течении линейная скорость
изменяется с расстоянием от оси трубки
по параболическому закону:
при
пуазейлевом течении линейная скорость
изменяется с расстоянием от оси трубки
по параболическому закону: ![]() .
Средняя линейная скорость - это величина
такой линейной скорости, которая, будучи
умноженной на площадь поперечного
сечения трубки, даст ту же объёмную
скорость течения Q,
что и формула Пуазейля:
.
Средняя линейная скорость - это величина
такой линейной скорости, которая, будучи
умноженной на площадь поперечного
сечения трубки, даст ту же объёмную
скорость течения Q,
что и формула Пуазейля: ![]() .
Откуда:
.
Откуда: ![]() ;
;
![]() .
Учтём
формулу для скорости сдвига в
цилиндрической трубке на стенке трубки:
.
Учтём
формулу для скорости сдвига в
цилиндрической трубке на стенке трубки:
![]() .
Подставим данные из условия задачи в
расчётную формулу и получим ответ:
.
Подставим данные из условия задачи в
расчётную формулу и получим ответ:
![]() .
.
2.49.
Поскольку указанное в условии задачи
число Рейнольдса превышает критическое
для цилиндрической трубы, то будем
считать, что максимальная линейная
скорость была использована для расчёта
этого числа. Тогда: ![]() .
Подставим данные из условия задачи в
расчётную формулу.
.
Подставим данные из условия задачи в
расчётную формулу. ![]() .
Получим ответ:
.
Получим ответ:
![]() .
.
2.50.
Будем считать моделью кровеносного
сосуда цилиндрическую трубку. Из формулы
Пуазейля для цилиндрической трубки
получается формула гидродинамического
сопротивления: ![]() .
Тогда искомое отношение гидродинамических
сопротивлений n:
.
Тогда искомое отношение гидродинамических
сопротивлений n:![]() .
Подставим данные из условия задачи в
расчётную формулу
.
Подставим данные из условия задачи в
расчётную формулу ![]() .
Получим ответ:
.
Получим ответ:
![]() .
.
2.51.
Указание на ламинарный режим течения
интерпретируем, как возможность
использовать для решения формулу
Пуазейля: ![]() .
Из формулы Пуазейля получим выражение
для разности давлений ∆P:
.
Из формулы Пуазейля получим выражение
для разности давлений ∆P:
![]() .
Отдадим себе отчёт в том, что разность
давлений в данном случае обусловлена
разностью гидростатического давления
и давления в вене: ∆P
= ρ·g·h
- Pвен.
Получим выражение для высоты капельницы
над постелью больного:
.
Отдадим себе отчёт в том, что разность
давлений в данном случае обусловлена
разностью гидростатического давления
и давления в вене: ∆P
= ρ·g·h
- Pвен.
Получим выражение для высоты капельницы
над постелью больного: ![]() .
Подставим в получившееся выражение
числовые данные и получим окончательный
результат, используя единицы СИ:
.
Подставим в получившееся выражение
числовые данные и получим окончательный
результат, используя единицы СИ:

![]() .
.
2.52.
Будем считать моделью кровеносного
сосуда цилиндрическую трубку. Из формулы
Пуазейля для цилиндрической трубки
получается формула гидродинамического
сопротивления: ![]() .
Гидродинамическое сопротивление,
приходящееся на единицу длины
.
Гидродинамическое сопротивление,
приходящееся на единицу длины![]() .
Гидродинамическое сопротивление
единицы длины до разветвления
.
Гидродинамическое сопротивление
единицы длины до разветвления ![]() Гидродинамическое сопротивление
единицы длины после разветвления
Гидродинамическое сопротивление
единицы длины после разветвления ![]() Тогдаискомое отношение гидродинамических
сопротивлений n:
Тогдаискомое отношение гидродинамических
сопротивлений n:![]() .
Подставим данные из условия задачи в
расчётную формулу
.
Подставим данные из условия задачи в
расчётную формулу ![]() .
Получим ответ:
.
Получим ответ:![]() .
.
2.53.
Будем считать моделью кровеносного
сосуда цилиндрическую трубку. Из формулы
Пуазейля для цилиндрической трубки
получается формула гидродинамического
сопротивления: ![]() .
Тогдаискомое отношение гидродинамических
сопротивлений n:
.
Тогдаискомое отношение гидродинамических
сопротивлений n:![]() .
Подставим данные из условия задачи в
расчётную формулу
.
Подставим данные из условия задачи в
расчётную формулу ![]() .
Получим ответ:
.
Получим ответ:![]() .
.
2.54.
Воспользуемся чисто резистивной
моделью кровообращения с сосредоточенными
параметрами. Из формулы Пуазейля
следует, что в рамках этой модели ![]() В
формуле
В
формуле ![]() -артериальное давление,
-артериальное давление, ![]() - объёмная скорость течения,
- объёмная скорость течения, ![]() - периферическое сопротивление.
- периферическое сопротивление. ![]()
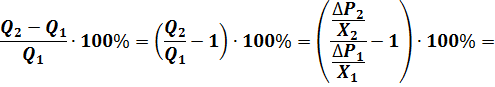
![]()
![]()
![]() .
Ответ: минутный объём циркуляции (одна
из мер объёмной скорости течения)
уменьшился на 4,5%.
.
Ответ: минутный объём циркуляции (одна
из мер объёмной скорости течения)
уменьшился на 4,5%.
2.55.
Перфузия ─── perfusio
(обливание, вливание)
- пропускание крови (или кровезамещающей
жидкости) через кровеносные сосуды
органа, части тела или всего организма.
В задаче воспроизведены основные черты
метода физиологии кровообращения,
который называют резистографией. Кровь
является неньютоновской жидкостью, но
при скоростях сдвига в несколько тысяч
обратных секунд её кажущаяся вязкость
с увеличением скорости сдвига перестаёт
меняться. Это предельное значение
кажущейся вязкости называется
асимптотической вязкостью. При решении
задачи будем исходить из формулы
Пуазейля как физической основы чисто
резистивной модели кровообращения с
сосредоточенными параметрами:![]() .
.
![]() .
Далее будем считать, что при неизменном
перфузионном давлении
.
Далее будем считать, что при неизменном
перфузионном давлении ![]() радиус эквивалентной трубкиR
не изменяется, скорости сдвига достаточно
высокие, длина эквивалентной трубки l
не изменяется.
радиус эквивалентной трубкиR
не изменяется, скорости сдвига достаточно
высокие, длина эквивалентной трубки l
не изменяется.  ,
,
![]() .
Подставим данные из условия задачи в
расчётную формулу
.
Подставим данные из условия задачи в
расчётную формулу ![]() .
.
Получим
ответ:
![]()
![]() .
.
2.56.
Будем считать моделью кровеносного
сосуда цилиндрическую трубку. Из формулы
Пуазейля для цилиндрической трубки
получается формула гидродинамического
сопротивления: ![]() .
Гидродинамическое сопротивление,
приходящееся на единицу длины
.
Гидродинамическое сопротивление,
приходящееся на единицу длины![]() .
Гидродинамическое сопротивление
единицы длины первого участка
.
Гидродинамическое сопротивление
единицы длины первого участка ![]() Гидродинамическое сопротивление
единицы длины второго участка
Гидродинамическое сопротивление
единицы длины второго участка ![]() Тогдаискомое отношение гидродинамических
сопротивлений n:
Тогдаискомое отношение гидродинамических
сопротивлений n:![]() .
Подставим данные из условия задачи в
расчётную формулу
.
Подставим данные из условия задачи в
расчётную формулу ![]() .
Получим ответ:
.
Получим ответ:![]() .
.
