Численные методы

Численные методы.

1.Источники погрешностей. Абсолютная и относительная погрешность числа. Значащие и

верные цифры.

При решении различных задач на компьютере, невозможно получить абсолютно точное значение y*, оно всегда содержит некую погрешность. Это следует из ограничения разрядности компьютера.

Причины погрешностей:

-математическая модель является лишь приблизительным описанием реального процесса. Характеристики процесса, вычисленные в рамках принятой модели, заведомо отличаются от истинных характеристик, причем их погрешность зависит от степени адекватности модели реальному процессу.

-исходные данные, как правило, содержат погрешности, поскольку они получаются либо в результате экспериментов (измерений), либо являются результатом решения некоторых вспомогательных задач.

-применяемые для решения задачи методы в большинстве случаев являются приближенными. Найти решение возникающей на практике задачи в виде конечной формулы возможно только в отдельных, очень упрощенных ситуациях.

-при вводе исходных данных в компьютер, выполнении арифметических операций и выводе результатов на печать производятся округления.

Пусть а – точное значение некоторой величины, а* - известное приближенное значение. Тогда абсолютная погрешность равна (a*)=|a-a*|. Однако по абсолютной погрешности нельзя сказать, большая погрешность или малая. Для этого существует относительная погрешность:

.

Значащими цифрами числа а* называют все цифры в его записи, начиная с первой ненулевой слева. ( . Значащую цифру числа а* называют верной, если

абсолютная погрешность числа не превосходит единицы разряда, соответствующей этой цифре (если , то числа 00 имеет 4 верные значащие цифры).

Количество верных значащих цифр числа тесно связано со значением его относительной погрешности. Если число а* содержит N верных значащих цифр, то справедливо неравенство

. Для того, чтобы число а* содержало N верных значащих цифр,

2. Погрешность вычисления функции одной переменной. Постановка задачи. Доказательство формулы.

Доказательство: Оценка вытекает из формулы конечных приращений Лагранжа:

Формулы для границ погрешностей функции f(x) одной переменной являются частным случаем при m=1:

.

3. Погрешность вычисления функции нескольких переменных. Обусловленность вычислительной задачи. Число обусловленности для задачи вычисления значения функции.

Доказательство: Оценка вытекает из формулы конечных приращений Лагранжа:

Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных. Задачу называют хорошо обусловленной, если малым погрешностям входных данных отвечают малые погрешности решения, и наоборот. Число

обусловленности можно интерпретировать как коэффициент возможного возрастания погрешностей в решении по отношению к вызвавшим их погрешностям входных данных.

Пусть между абсолютными погрешностями входных данных x и решения y установлено неравенство

Тогда величина называется абсолютным числом обусловленности. Если же установлено неравенство

Тогда величина называется относительным числом обусловленности. Чаще под числом обусловленности понимают относительное число обусловленности. Для плохо обусловленной задачи v>>1.

4. Особенности машинной арифметики. Понятия машинной бесконечности, машинного нуля, машинного эпсилон.

1) Системы счисления: принятый способ записи чисел состоит в представлении их упорядоченным набором цифр. В привычной нам десятичной системе счисления вещественное число х представляют последовательностью символов, которая начинается со знака (+ или -) и продолжается цепочкой десятичных цифр и , разделенных десятичной точкой

Здесь каждой позиции (разряду), которую занимает цифра относительно десятичной точки, отвечает определенная степень числа 10. Для хранения числа в памяти компьютера отводится поле стандартной длина (машинное слово), в котором число записывают в виде последовательности двоичных цифр. По форме представления, способу хранения и реализации арифметических операций существенно различаются на два типа используемых в компьютерах чисел: целые и вещественные.

а) представление целых чисел. Целое число n представляют в виде

, где L – некоторое стандартное для компьютера целое число, - двоичные цифры. Всего для хранения числа n отводят s=L+2 разрядов (один из них для хранения знака). Максимальное число, представимое в компьютере есть . Операции сложения, вычитания и умножения над целыми числами реализованы так, что если результат не превышает по модулю число , то он получается точным.

б) представление вещественных чисел. В современных компьютерах для вещественных чисел принята форма представления с плавающей точкой, когда каждое число представляют в виде

Здесь γ – двоичные цифры. Как правило, число x нормализуется так, чтобы , и поэтому в памяти компьютера хранятся только значащие цифры соответственного нормализованного числа. Число называют мантиссой числа х. В представлении (1) p –

целое число, называемое двоичным порядком. целое число, называемое двоичным порядком.

.

представления). Величина играет в вычислениях на компьютере фундаментальную роль; ее называют относительной точностью компьютера, или машинным эпсилоном.

Погрешность арифметических операций над числами с плавающей точкой равна

, где вместо может быть любая другая операция.

5. Решение нелинейных уравнений. Постановка задачи, основные этапы решения. Скорость сходимости итерационного метода. Интервал неопределенности корня.

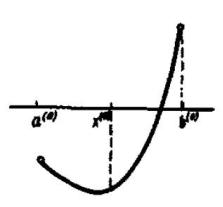
Корнем (или решением) уравнения f(x)=0 называется значение , при котором f( )=0.

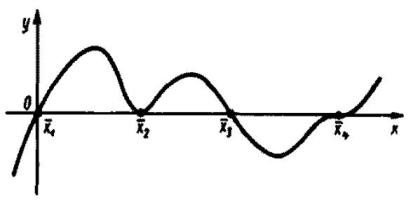
функции с осью Ох. Корень называется простым если график пересекает ось Ох под ненулевым углом, и кратным, если пересечение происходит под нулевым углом.

В конкретной задаче часто интерес представляют не все корни уравнения, а лишь некоторые из них. Тогда постановку задачи уточняют, какие из корней подлежат определению (положительные корни, корни из заданного интервала, максимальный из корней и т.д.).

Основные этапы решения

Решение задачи отыскания корней нелинейного уравнения осуществляется в два этапа. Первый этап называют этапом локализации корней, второй – этапом итерационного уточнения корней.

Локализация корней. Отрезок [a,b], содержащий только один корень уравнения, называют отрезком локализации корня . Цель этапа локализации считается достигнутой, если для каждого из подлежащих определению корней удалось указать отрезок локализации (его длину стараются по возможности сделать минимальной). Но прежде чем приступать к локализации стоит провести предварительное исследование, имеется ли решение уравнения, сколько их и как они расположены на числовой оси.

Теорема: пусть функция f непрерывна на отрезке [a,b] и принимает на его концах значения разных знаков, т.е. f(a)*f(b)<0. Тогда отрезок [a,b] содержит по крайней мере один корень уравнения f(x)=0.

Итерационное уточнение корней. На этом этапе для вычисления каждого из корней с точностью ε>0 используют тот или иной итерационный метод, позволяющий построить

предыдущих приближений. Заметим, что для построения итерационной последовательности

Скорость сходимости – одна из важнейших характеристик итерационных методов. Говорят, что метод сходится со скоростью геометрической прогрессии, знаменатель которой 0<q<1, если для всех n справедлива следующая оценка:

Пусть одношаговый итерационный метод обладает следующим свойством: существует σ-

окрестность корня такая, что если приближение принадлежит этой окрестности, то справедлива оценка:

Где C>0 и - постоянные. В этом случае р называют порядком сходимости метода.

Лемма 1. Пусть одношаговый итерационный метод обладает линейной скоростью сходимости в некоторой σ-окрестности корня . Тогда при любом выборе начального

приближения из σ-окрестности корня итерационная последовательность не выходит за пределы этой окрестности, метод сходится со скоростью геометрической прогрессии со знаменателем q=C<1 и имеет место следующая оценка погрешности:

Лемма 2. Пусть одношаговый итерационный метод в некоторой σ-окрестности корня

корня итерационная последовательность не выходит за пределы этой окрестности, метод сходится и справедлива оценка

окрестности знак вычисленного значения f*(x) не обязан совпадать со знаком f(x) и, следовательно, становится невозможным определить какое именно значение х из интервала обращает функцию в нуль. Этот интервал называется интервалом неопределенности корня .

6. Метод бисекции решения нелинейного уравнения: алгоритм, геометрическая иллюстрация, условия и скорость сходимости (с доказательством).

Описание метода: пусть требуется с заданной точность ε>0 найти корень уравнения. Отрезок локализации [a,b] (т.е. отрезок, содержащий только один корень ) будем считать заданным. Предположим что функция f непрерывна на отрезке и на его концах принимает значения разных знаков, т.е. f(a)f(b)<0.

Из этой оценки видно, что метод бисекции сходится со скоростью геометрической прогрессии, знаменатель которой равен q=1/2. По сравнению с другими методами, метод бисекции сходится довольно медленно.

Критерий окончания: Итерации следуют вести до тех пор, пока не будет выполнено неравенство . При его выполнении в силу оценки можно принять за приближение к корню с точностью ε.

7. Метод простой итерации решения нелинейного уравнения. Достаточное условие сходимости, априорная и апостериорная оценки погрешности (с доказательствами), критерий окончания, приведение к виду, удобному для итераций.

Описание метода: чтобы применить метод простой итерации для решения нелинейного уравнения, необходимо преобразовать это уравнение к виду x=ϕ(x). Это преобразование (приведение уравнение к виду, удобному для итераций) можно выполнить различными способами. Функцию ϕ называют итерационной функцией.

этот процесс неограниченно, получаем последовательность приближений к корню, вычисляемых

по формуле . Если существует предел построенной последовательности

Сходимость метода:

Теорема: Пусть в некоторой σ-окрестности корня функция ϕ дифференцируема и удовлетворяет неравенству

Где 0<q<1 – постоянная. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод

сходится со скоростью геометрической прогрессии и справедлива следующая оценка погрешности:

Доказательство: использую формулу конечных приращений Лагранжа, получаем

Оценка погрешности является априорной. Она показывает, что метод простой итерации сходится со скоростью геометрической прогрессии, знаменатель которой равен q. Чем меньше q, тем выше скорость сходимости.

Доказательство: в силу равенства из предыдущего доказательства имеем

Откуда

Взяв модуль от левой и правой частей этого равенства, и воспользовавшись неравенством

И получаем требуемое соотношение.

Приведение уравнения к виду, удобному для итераций:

Предположим что производная f’ на отрезке [a,b] непрерывна и положительна. Тогда существуют положительные постоянные m и M такие, что 0<m<f’(x)<M при x принадлежащему

8. Метод Ньютона решения нелинейного уравнения. Теорема о сходимости (без доказательства), априорная и апостериорная оценки (с доказательствами), критерий окончания, геометрическая интерпретация, трудности использования.

Метод Ньютона делится на два подхода: метод касательных и метод линеаризации.

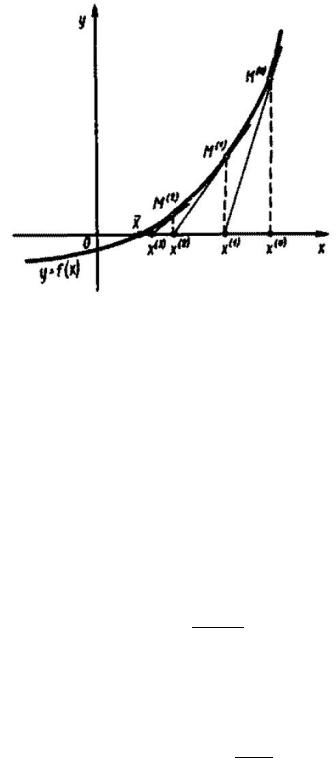
Метод касательных:

примем абсциссу точки пересечения касательной с осью Ох. Продолжая этот процесс далее,

Выражая из него , получаем расчетную формулу метода Ньютона:

Метод линеаризации: метод Ньютона можно рассматривать как итерационный метод.

Пусть приближение уже получено. Представим функцию в окрестности точки по формуле Тейлора:

Здесь ξ – некоторая точка, расположенная между x и . Заменяя в уравнении f(x)=0 функцию f(x) главной линейной частью разложения, получаем линейное уравнение

Теорема о сходимости: пусть - простой корень уравнения f(x)=0, в некоторой окрестности которого функция f дважды непрерывно дифференцируема. Тогда найдется такая малая σ-

окрестность корня , что при произвольной выборе начального приближения из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка

Означающая, что метод сходится с квадратичной скоростью. Следствием оценки является априорная оценка

непрерывности функции f’ и f’’ найдется δ-окрестность корня, в которой при некоторых

Подставляя x= в формулу Тейлора, получаем равенство

Тогда, приравнивая модули обеих частей этого равенства и используя условия ограниченность модулей производных, приходим к неравенству

Откуда следует справедливость оценки.

На практике предпочтительнее использование простой апостериорной оценки