
Численные методы
.pdf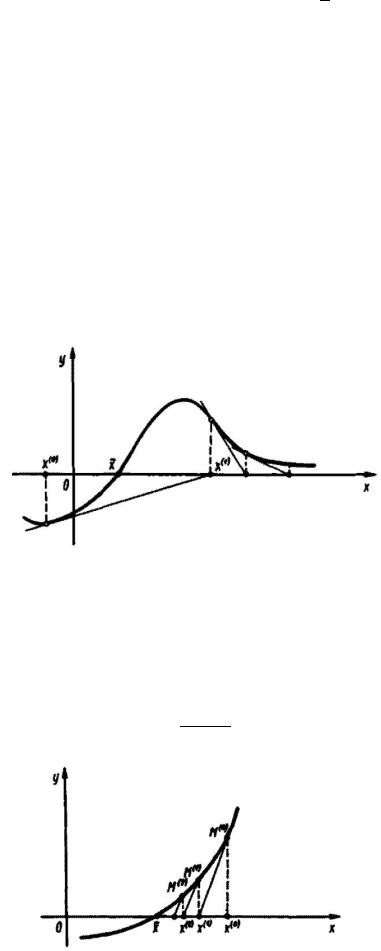
Поэтому применяя неравенство априорной оценки получаем цепочку неравенств
Из которой вытекает апостериорной оценки. Вычисление нужно вести до тех пор, пока не окажется выполнено неравенство
Трудности использования:
1)Иногда невозможно найти аналитическое выражение для f(x) (взять производную).
2)Метод Ньютона обладает только локальной сходимостью, то есть область его
сходимости является некоторая малая σ окрестность корня и для гарантии сходимости необходимо выбирать хорошее начальное приближение. Неудачный выбор может дать расходящуюся последовательность.
9) Модификации метода Ньютона (упрощенный метод Ньютона, метод ложного положения, метод секущих, метод Стеффенсена). Поиск кратных корней.
Упрощенный метод Ньютона: если производная непрерывна, то ее значение вблизи простого корня почти постоянно. Поэтому можно попытаться вычислить f’ лишь однажды в
точке , а затем заменить в формуле значение постоянной .
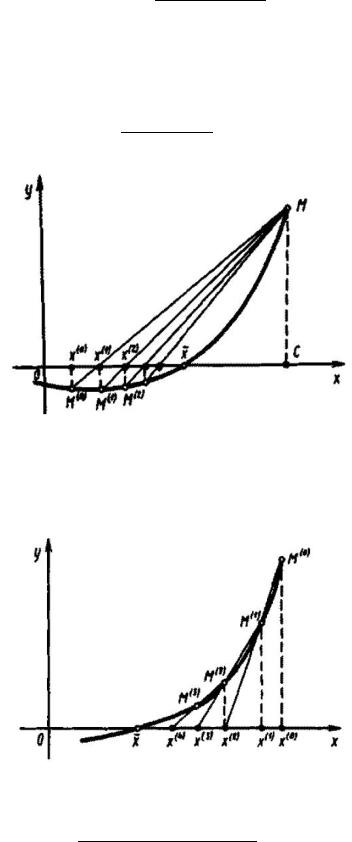
В основе следующих модификаций лежит приближенное равенство
Верно при условии и следует из определения производной. Пусть с – фиксированная точка, в окрестности корня. Заменим производную в формуле метода Ньютона приближенным равенством, полагая . В результате получим метод ложного положения:
Метод секущих: |
приравниваем к |
и получаем расчетную формулу |
||
|
|
|
|
|
Метод Стефенсена: итерационная формула имеет вид
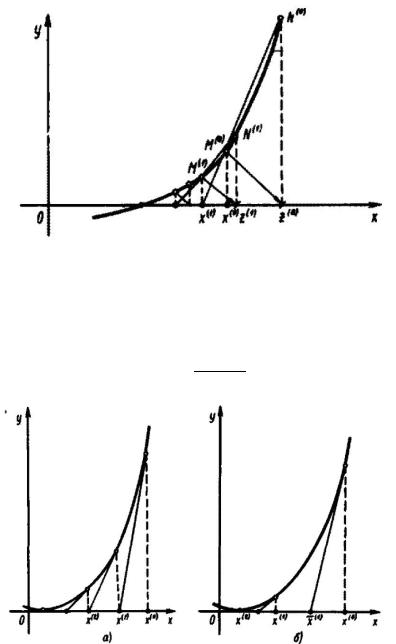
Уточнение метода Ньютона для случая кратного корня
При m>1 скорость сходимости стандартного метода становится линейной. Чтобы сохранить квадратичную скорость, метод Ньютона нужно модифицировать следующим образом:
а) стандартный метод, б) уточненный метод.
10) Решение СЛАУ. Постановка задачи. Нормы векторов и матриц. Понятие о прямых и итерационных методах решения.
Ввычислительной линейной алгебре традиционно выделяют четыре основные задачи:
1)Решение систем линейных алгебраических уравнений
2)Вычисление определителей
3)Нахождение обратных матриц
4)Определение собственных значений и собственных векторов
В последнее время к ним добавились еще две:
5)Линейная задача метода наименьших квадратов
6)Вычисление сингулярных чисел и сингулярных векторов.

Норма вектора: говорят, что в |
задана норма, если каждому вектору x из |
сопоставлено |
|
вещественное число |
, называемое нормой вектора х и обладающее следующими свойствами: |
||
1), причем равно нулю тогда и только тогда, когда х=0
2) |
для любого вектора х и любого числа a |
3) |
для любых векторов х и у. |
Наиболее употребительные нормы:
Справедливы неравенства: |
. |
|
|
Норма матрицы: Величина |
называется нормой матрицы А, |
подчиненной норме векторов, введенной в . |
|
|
|
Свойства те же, что и у норм векторов, но дополнительно к этому: |
|
4) |
для любых матриц А и В |
|
5) |
Для любой матрицы А и любого вектора х справедливо неравенство |
|
Вычисление норм:
Понятие о прямых и итерационных методах решения
Прямой метод решения систем линейных алгебраических уравнений с вещественными коэффициентами
В матричной форме записи эта система имеем вид Ax=b. Суть прямого метода – отыскание вектора х, являющегося решением системы, по входному данному – вектору b.
Итерационные методы применяются главным образом для задач большой размерности, когда использование прямых методов усложнено.
11) Обусловленность задачи решения СЛАУ (с доказательством). Свойства нормального числа обусловленности матрицы.

Лемма: для погрешности приближенного решения системы справедлива оценка
Где r=b-Ax* - невязка, отвечающая x*.
Теорема: пусть х* - точное решение системы Ax*=b, в которой правая часть b* является приближенным к b. Тогда верны следующие оценки абсолютной и относительной погрешностей:
Где |
|
|
|
|
. |
|
|
|
|
||||
|
Доказательство: в рассматриваемом случае r=b-Ax*=b-b* и неравенство из леммы |
|||||
принимает вид (1). Разделив теперь обе части (1) на |
и записав в виде приходим к оценке (2). |
|||||
Вычислим максимальное значение естественного числа обусловленности, использовав определение нормы матрицы
Полученную величину принято называть стандартным числом обусловленности матрицы А и обозначать v(A) или cond(A). Таким образом
Следствие: в условиях теоремы о погрешностях справедлива оценка
Для ее доказательства достаточно воспользоватся относительной оценкой и заметить, что в силу равенства (3) верно неравенство .
Систему и матрицу А принято называть плохо обусловленными, если cond(A)>>1.
Свойства числа обусловленности:
1)Для единичной матрицы cond(E)=1
2)Справедливо неравенство
3)Число обусловленности матрицы А не меняется при умножении матрицы на произвольное число не равное нулю.
Если с погрешностью заданы как правая часть, так и сама матрица, то
12) Метод Гаусса (схема единственного деления). Трудоемкость метода.

Метод Гаусса состоит из двух основных этапов: прямой ход и обратный. Прямой ход заключатся в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Схема единственного деления:
Прямой ход состоит из m-1 шагов исключения.
1й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами
i=2,3,4,...,m. Предположим, что коэффициент |
не равен нулю. Будем называть его главным |
|
элементов 1го шага. Найдем величины |
|
|
|
|
|
Называемые множителями 1го шага. Вычтем последовательно из второго, третьего,…,m-го уравнения системы первое уравнение, умноженные на соответствующие величины, обращая в нуль все коэффициенты при во всех уравнениях, кроме первого.
2й шаг. Проделываем то же самое, только для и для i=3,4,…,m.
Аналогично проводятся остальные шаги. После (m-1)-го шага исключения получим систему уравнений, матрица которой является верхней треугольной. На этом вычисление прямого хода заканчивается.
Обратный ход. Из последнего уравнения системы находим . Подставляя найденное
значение |
в предпоследнее уравнение, получаем |
. Осуществляя обратную подстановку, |
|
далее последовательно находим |
. Вычисление неизвестных производится по |
||
формулам: |
|
|
|
Трудоемкость метода: Подсчитаем приближенно общее число Q арифметических операций прямого хода, считая размерность системы m достаточно большой:
Нетрудно увидеть, что для реализации обратного хода по формулам обратного хода нужно всего операций, что при больших m пренебрежимо мало по сравнению с числом операций прямого хода. Таким образом для реализации метода Гаусса требуется примерно (2/3) арифметических операций.
13) Метод Гаусса с выбором главного элемента (полный и частичный выбор). Трудоемкость.
Частичный выбор
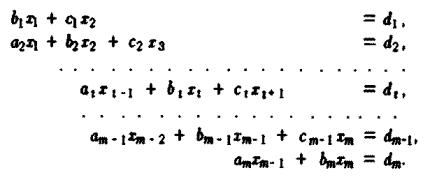
Описание метода: на k-m шаге прямого хода коэффициенты уравнений системы с номери i=k+1,…,m преобразуются по формулам
Во избежание сильного роста коэффициентов системы и связанных с этим погрешностей
нельзя допускать появления больших множителей . |
|
|
В методе Гаусса с выбором главного элемента по столбцу гарантируется, что |
для |
|
всех k=1,2,…,m-1 и i=k+1,…,m. Отличие этого варианта метода Гаусса от схемы единственного |
|
|
деления в том, что на k-м шаге исключения в качестве главного элемента выбирается |
|
|
максимальный по модулю коэффициент |
при неизвестной в уравнениях с номерами |
|
i=k,k+1,…,m. |
|
|
Полный выбор
В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1м шаге метода среди элементов матрицы определяют максимальный по модулю
элемент |
. Первое уравнение системы и уравнение с номером меняют местами. Далее |
||
стандартным образом производят исключение неизвестного из всех уравнений, кроме |
|||
первого. |
|
|
|
На k-м шаге метода среди коэффициентов |
при неизвестных в уравнениях системы с |
||
номерами i=k,…,m выбирают максимальный по модулю коэффициент |
. Затем k-е уравнение |
||
и уравнение, содержащее найденный коэффициент меняют местами и исключают неизвестное из уравнений с номерами i=k+1,…,m.
Гарантия хорошей обусловленности достигается ценой значительных затрат на выбор
главных элементов. Для этого, дополнительно к |
|
арифметическим действиям требуется |
|
|
|||
произвести примерно |
операций сравнения. |
|
|
14) Трехдиагональные СЛАУ. Метод прогонки: вывод расчетных формул, трудоемкость, условия применения (без доказательства).
Вывод расчетных формул. Преобразуем первое уравнение системы к виду

Где |
, |
. Подставим полученное для выражение во второе уравнение |
системы: |
|
|
Преобразуем к виду
Где |
, |
. |
Это выражение подставляем в третье уравнение системы и т.д. На i-м шаге этого процесса 1<i<m i- е уравнение системы преобразуется к виду
Где |
, |
. |
|
|
На m-м шаге подстановка в последнее уравнение выражения |
дает |
|
Откуда можно определить значение
Алгоритм прогонки: сделанные преобразования позволяют организовать вычисление методом прогонки в два этапа:
Прямой ход: вычисление прогоночных коэффициентов:
Обратный ход дает значения неизвестных. Сначала |
, а затем значения остальных |
неизвестных вычисляют по формуле |
|
Для реализации вычислений по формулам требуется примерно 8m арифметических
операций, тогда как в методе Гаусса это число составляет примерно .
Теорема: пусть коэффициенты системы удовлетворяют следующим условиям диагонального преобладания:
Тогда |
и |
для всех i=1,2,…,m. |
15) Метод простой итерации (Якоби) решения СЛАУ. Приведение к виду, удобному для итераций, достаточное условие сходимости, априорная и апостериорная оценки (с доказательствами), критерий окончания.
Приведение к виду, удобному для итераций
Для того чтобы применить метод простой итерации к решению системы линейных алгебраических
уравнений |
с квадратной невырожденной матрицей А, необходим перобразовать эту |
||
систему к виду x=Bx+c. Здесь B квадратная матрица с элементами |
c- |
||
вектор столбец с элементами |
. |
|
|
В развернутой форме записи система имеет следующий вид:
Самый простой способ приведения системы к виду удобному для итераций состоит в следующем. Из первого уравнения системы выразим неизвестное
Из второго уравнения выразим неизвестное
И.т.д. в результате получим систему
Сходимость метода простой итерации
Теорема: Пусть выполнено условие
Тогда |
|
|
|
||
1)Решение |
|
, системы существует и единственно |
|
|
|
|
|
|
|
||
2)при произвольном начальном приближении |
метод простой итерации сходится и |
||||
справедлива оценка погрешности |
|
|
|
||
|
|
|
|
|
|
Доказательство:

1)из курса линейной алгебры известно, что система линейных алгебраических уравнений имеет единственное решение при любой правой части тогда и только тогда, когда соответствующая однородная система имеет только нулевое решение. Пусть х – решение однородной системы x=Bx
тогда |
|
. Так как по условию |
|
|
|
|
|
это неравенство возможно только |
||
при |
и тем самым первое утверждение теоремы доказано. |
|||||||||
2)Вычитая из равенства |
равенство |
|
=B |
|
|
+c, получаем |
||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Вычисляя норму левой и правой частей этого равенства и используя неравенство
имеем
т.к. это неравенство верно для всех k |
то |
||
|
|
|
|
Справедливость неравенства(оценки погрешности) установлена. Учитывая, что |
|
|
не |
|||
зависит от n а |
получаем из него, что |
|
при |
. |
|
|
|
|
|||||
Апостериорная оценка погрешности
Если выполняется ||B|| то справедлива апостериорная оценка погрешности
Доказательство: k = n-1
Тогда
Для завершения доказательства осталось заметить, что полученное неравенство эквивалентно неравенству, что написанному выше.
Критерий окончания
16.Метод Зейделя решения СЛАУ. Достаточные условия сходимости, априорная и апостериорная оценки ( с доказательствами), критерий окончания. Геометрическая интерпретация для системы двух уравнений. Метод релаксации.
