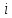Алгоритм
Шаг 1.
Положить
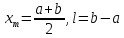 .
Вычислить
.
Вычислить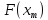 .
.
Шаг 2.
Положить
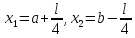 .
Заметим, что точки
.
Заметим, что точки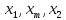 делят интервал
делят интервал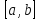 на
на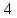 равные части. Вычислить значения
равные части. Вычислить значения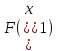 и
и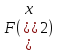 .
.
Шаг 3.
Сравнить
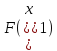 и
и .
.
Если
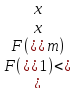 ,
исключить интервал
,
исключить интервал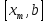 ,
положив
,
положив .
При этом средней точкой нового интервала
поиска становится точка
.
При этом средней точкой нового интервала
поиска становится точка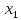 ,
следовательно, необходимо положить,
что
,
следовательно, необходимо положить,
что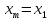 .
Перейти к шагу 5.
.
Перейти к шагу 5.
Если
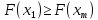 ,
перейти к шагу 4.
,
перейти к шагу 4.
Шаг 4.
Сравнить
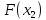 и
и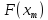 .
.
Если
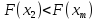 ,
исключить интервал
,
исключить интервал ,
положив
,
положив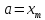 .
Т.к. в середине нового интервала
оказывается
.
Т.к. в середине нового интервала
оказывается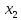 ,
положить
,
положить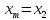 .
Перейти к шагу 5.
.
Перейти к шагу 5.
Если
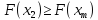 ,
исключить интервалы
,
исключить интервалы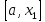 и
и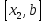 ,
положив
,
положив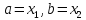 .
Заметим, что
.
Заметим, что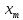 продолжает оставаться средней точкой
нового интервала. Перейти к шагу 5.
продолжает оставаться средней точкой
нового интервала. Перейти к шагу 5.
Шаг 5.
Вычислить
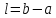 .
Если величина
.
Если величина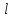 меньше заданной точности
меньше заданной точности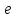 ,
закончить поиск. В противном случае
перейти к шагу 2.
,
закончить поиск. В противном случае
перейти к шагу 2.
Пример
Пусть
 определена на отрезке
определена на отрезке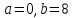 .
Найти
.
Найти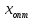 с точностью
с точностью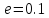 .
.
Итерация 1.
Шаг 1.
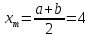
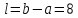
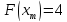
Шаг 2.
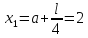

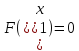

Шаг 3.
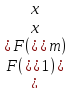 следовательно, исключается интервал
следовательно, исключается интервал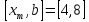 ,
поэтому
,
поэтому
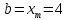
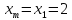
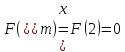
Переходим к шагу 5.
Шаг 5.
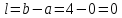
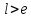 следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком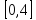 ,
при этом
,
при этом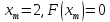 .
.
Итерация 2.
Шаг 2.
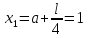

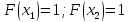
Шаг 3.
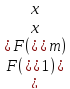 следовательно, переходим к шагу 4.
следовательно, переходим к шагу 4.
Шаг 4.
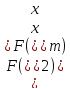 следовательно, исключаются интервалы
следовательно, исключаются интервалы ,
поэтому новое значение
,
поэтому новое значение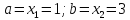 ,
старые значения сохраняются для
,
старые значения сохраняются для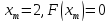 .
Переходим к шагу 5.
.
Переходим к шагу 5.
Шаг 5.

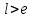 следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком ,
при этом
,
при этом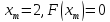 .
.
Итерация 3.
Шаг 2.
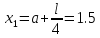


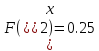
Шаг 3.
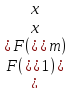 следовательно, переходим к шагу 4.
следовательно, переходим к шагу 4.
Шаг 4.
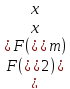 следовательно, исключаются интервалы
следовательно, исключаются интервалы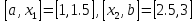 ,
поэтому новое значение
,
поэтому новое значение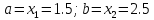 ,
старые значения сохраняются для
,
старые значения сохраняются для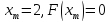 .
Переходим к шагу 5.
.
Переходим к шагу 5.
Шаг 5.
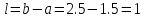
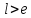 следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком .
.
Последующие
итерации аналогичны проделанным и далее
не рассматриваются. Окончание процедуры
происходит при выполнении условия
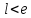 на шаге 5.
на шаге 5.
Выводы
В нашем
примере за 3 итерации (т.е. при шести
вычислениях функции
 )
исходный интервал поиска сузился с 8 до
1. Как видите, метод дихотомии позволяет
довольно быстро попасть в область
экстремума. Так для определения положения
экстремума с точность в
)
исходный интервал поиска сузился с 8 до
1. Как видите, метод дихотомии позволяет
довольно быстро попасть в область
экстремума. Так для определения положения
экстремума с точность в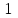 от длины начального интервала надо
сделать всего 14 измерений показателя
качества (это 7 итераций дихотомии), т.к.
от длины начального интервала надо
сделать всего 14 измерений показателя
качества (это 7 итераций дихотомии), т.к.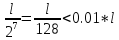 .
Это намного лучше, чем метод сканирования,
который требует 101 измерение.
.
Это намного лучше, чем метод сканирования,
который требует 101 измерение.
Алгоритм получения границ начального интервала неопределённости
Если начальный интервал, содержащий точку мининмума, неизвестен, его можно получить. Поиск граничных точек начального интервала производится обычно с помощью эвристических методов. Рассмотрим один из них.
Алгоритм полученияначального интервала состоит из двух этапов:
Выбор «удачного» направления
Движение в этом направлении до получения точки минимума
Исходными
данными являются начальная точка
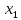 и величина шага
и величина шага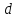 .
Рассмотрим шаги первого этапа алгоритма
получения начального интервала.
.
Рассмотрим шаги первого этапа алгоритма
получения начального интервала.
Шаг 1.
Вычислить
значение функции в начальной точке
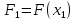
Шаг 2.
Вычислить
значения аргумента и функции после шага
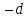 .
.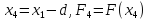 .
.
Шаг 3.
Вычислить
значения аргумента и функции после шага
 .
.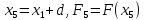
Шаг 4.
Шаг 4.1
Если
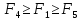 ,
то шаг
,
то шаг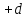 удачное направление. Оставляем его и
обозначим
удачное направление. Оставляем его и
обозначим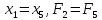 .
.
Шаг 4.2
Если
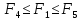 ,
то шаг
,
то шаг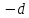 удачное направление. Оставляем его и
обозначим
удачное направление. Оставляем его и
обозначим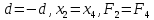 .
.
Шаг 4.3
Если
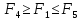 ,
то начальный интервал уже найден: точка
минимума лежит между
,
то начальный интервал уже найден: точка
минимума лежит между и
и .
.
Шаг 4.1
Если
 ,
то функция
,
то функция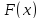 не является унимодальной и задачу надо
решать другим методом.
не является унимодальной и задачу надо
решать другим методом.
На втором этапе – движения в выбранном направлении до получения интервала, содержащего точку минимума, -делается ряд шагов увеличивающейся длины. Алгоритм второго этапа для получения начального интервала неопределённости.
Шаг 1.
Переприсвоение:
 .
.
Шаг 2.
Расчёт
новой длины шага:
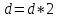 .
.
Шаг 3.
Расчёт
аргумента и функции в третьей точке:
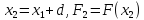 .
.
Шаг 4.
Сравнение
 и
и :
:
если
 ,
перейти к шагу 1
,
перейти к шагу 1если
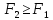 ,
окончание поиска: интервал неопределённости
равен
,
окончание поиска: интервал неопределённости
равен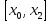
Эффективность поиска граничных точек непосредственно зависит от величины шага. Если шаг велик, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если шаг мал, то для определения граничных точек может потребоваться достаточно большой объём вычислений. Несомненным достоинством методов такого рода является то, что они основаны лишь на вычислении значений функции. При этом не требуется, чтобы исследуемые функции были дифференцируемы. Более того, допустимы случаи, когда целевую функцию нельзя даже записать в аналитическом виде.
Единственным
требование является возможность
определения значений
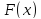 в заданных точках
в заданных точках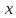 с помощью прямых расчётов или имитационных
экспериментов.
с помощью прямых расчётов или имитационных
экспериментов.
Пример
Решим вместе
с вами задачу на установление границ
начального интервала. Найти начальный
интервал неопределённости для функции
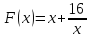 с начальной точкой
с начальной точкой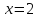 и величиной шага
и величиной шага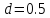 .
.
Выполним шаги первого этапа алгоритма.
Шаг 1.
Вычислим
значение функции в начальной точке:
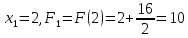 .
.
Шаг 2.
Вычислим
значение аргумента и функции слева от
начальной точки:
 .
.
Шаг 3.
Вычислим
значения аргумента и функции справа от
начальной точки:
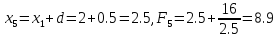 .
.
Шаг 4.
Сравним
значения функции в трёх точках:
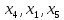 .
Получим
.
Получим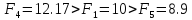 .
Т.е. функция убывает в направлении шага
.
Т.е. функция убывает в направлении шага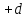 ,
а значит, это правильное направление и
нам надо двигаться в право по оси
,
а значит, это правильное направление и
нам надо двигаться в право по оси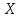 .
Принимаем:
.
Принимаем: .
.
Выполним второй этап алгоритма – движение в выбранном направлении до получения отрезка, содержащего точку минимума.
Итерация 1
Шаг 1.
Выполняем
присвоение:
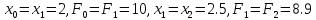 .
.
Шаг 2.
Расcчитываем
новую длину шага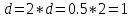 .
.
Шаг 3.
Находим в
третьей точке:
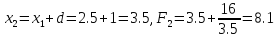 .
.
Шаг 4.
Сравниваем
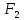 и
и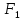 .
.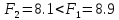 следовательно, надо вновь идти на шаг
1 и делать вторую итерацию.
следовательно, надо вновь идти на шаг
1 и делать вторую итерацию.
Итерация 2
Шаг 1.
Выполняем
присвоение:
 .
.
Шаг 2.
Расcчитываем
новую длину шага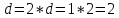 .
.
Шаг 3.
Находим в
третьей точке:
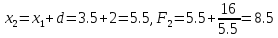 .
.
Шаг 4.
Сравниваем
 и
и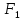 .
. .
Поскольку
.
Поскольку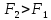 ,
процедуру поиска начального интервала
заканчиваем. Начальный интервал:
,
процедуру поиска начального интервала
заканчиваем. Начальный интервал: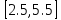 .
.
Метод сканирования
Метод
сканирования – это численный метод
оптимизации, в котором не требуется
знание априорной информации об исследуемой
функции. Будем считать, что с аналитическими
методами решения задач одномерной
оптимизации вы знакомы из курса
математического анализа. Мы же остановимся
именно на численных методах. Для
определённости будем рассматривать
задачу минимизации, поскольку известно,
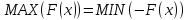 .
.
Существует
множество численных методов одномерной
оптимизации. Среди них есть более простые
и более сложные. Сложность метода зависит
от априорной информации о показателе
качества
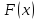 .
Если о функции
.
Если о функции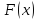 известно только то, что она имеет
экстремальный характер, и никакой другой
априорной информации нет, то при отыскании
экстремума единственным разумным
действием в такой ситуации будет
последовательное нахождение значения
критерия при всех допустимых значениях
известно только то, что она имеет
экстремальный характер, и никакой другой
априорной информации нет, то при отыскании
экстремума единственным разумным
действием в такой ситуации будет
последовательное нахождение значения
критерия при всех допустимых значениях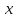 .
.
Поскольку
таких значений на отрезке
 бесконечное множество, то практически
перед решением задачи задаются точностью
определения оптимального значения
переменной
бесконечное множество, то практически
перед решением задачи задаются точностью
определения оптимального значения
переменной .
Обозначим данную точность через
.
Обозначим данную точность через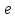 .
Тогда для отыскания экстремума следует
определить
.
Тогда для отыскания экстремума следует
определить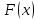 в
в равноотстоящих друг от друга на величину
равноотстоящих друг от друга на величину точках где целое число
точках где целое число задаётся округлением значения
задаётся округлением значения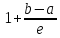 до ближайшего большего целого значения.
При этом значение реализуемой точности
решения
до ближайшего большего целого значения.
При этом значение реализуемой точности
решения определяется как:
определяется как: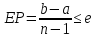 .
.
Значения
аргумента в
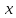 точках расчёт определяется по следующей
формуле:
точках расчёт определяется по следующей
формуле: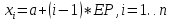 .
Крайние точки отрезка получаются при
.
Крайние точки отрезка получаются при и
и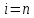 .
Из полученных значений функции выбирается
наименьшее значение. Номер наименьшего
значения и определяет оценку положения
экстремума с точностью не хуже, чем
заданная величина
.
Из полученных значений функции выбирается
наименьшее значение. Номер наименьшего
значения и определяет оценку положения
экстремума с точностью не хуже, чем
заданная величина .
.
Пример
Пусть
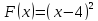 определена на отрезке
определена на отрезке .
Найти
.
Найти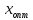 с точностью
с точностью .
Рассчитаем необходимое число точек,
для этого вычислим выражение
.
Рассчитаем необходимое число точек,
для этого вычислим выражение .
Округлив до ближайшего целого получаем
.
Округлив до ближайшего целого получаем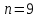 .
Реализуемая точность равна
.
Реализуемая точность равна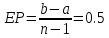 ,
что лучше заданной точности
,
что лучше заданной точности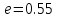 .
.
Рассчитаем
значение аргумента в 9 точках по формуле:
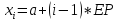 .
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
Рассчитаем значения функции в каждой точке:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
|
|
9 |
6.25 |
4 |
2.25 |
1 |
0.25 |
0 |
0.25 |
1 |
Сравнивая
значения функции в 9 точках, находим:
 .
.