Метод Фибоначчи

В этом разделе рассматривается метод Фибоначчи. Этот метод довольно часто используется не только в случае одномерной оптимизации, но и в процессе решения задач математического программирования, например, в многомерных задачах минимизации по заданному направлению.

С помощью численной процедуры, описанной в данном учебном курсе, непосредственно ищется минимум функции в некотором интервале, в котором предположительно лежит этот минимум. При этом метод Фибоначчи относятся к методам исключения интервалов, на которых заведомо отсутствует оптимум исследуемой функции. Кроме того в данных методах предполагается, что оптимизируемая функция является унимодальной.

В процессе применения методов исключения интервалов можно выделить две фазы:

• Фаза установления границ интервала, на котором реализуется процедура поиска. Это могут быть границы достаточного широкого интервала заведомо содержащего точку оптимума. В поисковых задачах оптимизации отрезок, на котором находится точка минимума, называют интервалом неопределённости.

• Фаза уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины (точности поиска экстремума).

На втором этапе, этапе уменьшения интервала, как раз и применяется метод Фибоначчи. В общем виде задача оптимизации ставится следующим образом: «Найти минимум унимодальной функции на замкнутом интервалепри заданном числе вычислений функции».

Краткое описание метода Фибоначчи

Предположим, что нужно определить минимум как можно точнее, т.е. с наименьшим интервалом неопределённости, но при этом можно выполнить только вычислений функции. Как следует расположить этиточек? Ясно, что надо сделать так, чтобы в последующих итерациях использовались точки, использованные на предыдущих итерациях. Предположим, что на интервале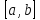известно значение функции в точке. Если можно вычислить значение функции только один раз (т.е.), то где поместить точку, для того чтобы получить наименьший интервал неопределённости после отбрасывания интервала, в котором оптимум не расположен?

Рассмотрим рисунок. Точки фиксированы. Предположим, что, а точкарасположена на интервале. Возможны два случая:

• , то интервал, на котором расположен оптимум, будетдлиной;

• , то новый интервал неопределённости –длиной;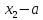

Поскольку не известно, какая ситуация справедлива, точку надо выбрать так, чтобы минимизировать наибольшую из длин:или. Достигнуть этого можно, сделав эти длины равными, т.е. поместивсимметрично относительно точки(в любом другом случае новый интервал будет большей величины).

Кроме того, при (прина последнем интервале) длина последнего интервала минимальна, если предпоследний интервал разделить пополам. Действительно, при этоми последний интервал неопределённости равен. Однако притрудно выбрать нужный интервал неопределённости, поскольку. Обычно точкииотстоят друг от друга на достаточном расстоянии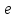, чтобы чётко зафиксировать, в какой точке интерваланаходится интервал неопределенности.

Предположим теперь, что можно вычислить значение функции раз. В этом случае стратегия поиска ясна с самого начала. Нужно поместить следующую точку внутри интервала симметрично относительно уже находящейся там точки. Парадоксально, но, чтобы понять, как следует начинать процедуру вычисления, необходимо разобраться в том, как следует кончать её.

Уже было показано, что на последнем -ом вычислении -ю точку (на поясняющем рисунке) следует поместить симметрично по отношению кточке (точке) на расстояниеиз условия различимостив этих точках.– это интервал нечувствительности на последней итерации, т.е. разница между аргументамиидвух экспериментов, при которых можно отличить значения функцийи.

Замечание: на первом этапе можно считать и точкурасположить в середине отрезка, а затем точку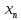расположить справа или слева от первой точки на достаточно малом расстояниине равном 0.

Из рисунка следует, что интервал неопределённости имеет длину . Тогда. На предыдущем этапе точкиидолжны быть смещены симметрично внутри интервалана расстояниеот концов. Следовательно,. Аналогично показывается, что. В общем случае, при. Таким образом:

В общем случае , где,- последовательность чисел Фибоначчи, определяемая как:для.

Если начальный интервал , то конечный:. Следовательно, произведявычислений функции, начальный интервал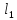уменьшается враз (пренебрегая малой величиной). Это наилучший результат. Если поиск начат с начальным интервалом, то его несложно продолжить, используя правило симметрии: на отрезкенеобходимо найти положение первой точки, которая размещается на расстоянииот правого конца интервала(ближе к точке), а вторая точка (точка) – на таком же расстоянииот левого конца интервала (ближе к точке). Значениеравно.

После того как найдено положение точек и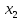, числа Фибоначчи больше не нужны. Используемое значениеможет определяться из практических соображений, но в любом случае должно выполняться:В противном случае на вычисление функциибудет напрасно тратиться время.