- •51.1. Понятие системы счисления. Позиционные и непозиционные системы счисления. Методы перевода чисел из одной системы счисления в другую.
- •52.1 Представление чисел с фиксированной и плавающей запятой. Диапазон и точность представления
- •52.2 Типы звеньев данных. Понятие звена данных.
- •52.3 Системы искусственного интеллекта. Методы представлениязнаний. Рассужденияизадачи.
- •53.1 Выполнение операции алгебраического сложения с плавающей запятой
- •53.2 Локальные вычислительные сети. Особенности. Основные распространенные протоколы, методы доступа
- •53.3 Определение базы данных. Уровни представления данных, принцип независимости данных. Схема базы данных
- •54.1 Умножение чисел со старших разрядов в прямом коде
- •Умножение с младших разрядов в дополнительном коде
- •Умножение со старших разрядов в дополнительном коде
- •55.1 Методы выполнения операции деления.
- •2 Деление двоичных чисел с фиксированной запятой
- •2.8. Деление двоичных чисел с плавающей запятой
- •55.2 Язык программирования php. Синтаксис. Основные операторы.
- •56.1 Основные положения и законы алгебры логики
- •56.2 Dhtml. JavaScript. Возможности и области применения
- •2. Моделированиеэкспоненциальнойслучайнойвеличины
- •1. Алгоритм реализации датчика дискретной с.В.
- •2. Пуассоновская с.В
- •58.1.Минимизация логической функции.
- •59.1 Синтез комбинационных логических схем в различных базисах.
- •59.2 Интерфейс программного обмена данными. Структура системной шины.
- •59.3. Реляционная алгебра. Sql
- •60.1.Основные характеристики и параметры интегральных логических элементов. Виды интегральных схем по функциональному назначению.
- •Итнернет технологии
- •2.1 Как работают механизмы поиска
- •60.3 Проектирование реляционной бд, функциональные зависимости, декомпозиция отношений, нормальные формы.
- •62.1 Законы Кирхгофа и преобразование электрических цепей на их основе.
- •63. 1 Электрические источники вторичного питания.
- •Трансформаторный (сетевой) источник питания
- •Габариты трансформатора
- •Достоинства трансформаторных бп
- •Недостатки трансформаторных бп
- •Импульсный источник питания
- •Достоинства импульсных бп
- •Недостатки импульсных бп
- •68.3 Понятие и принципы построения математической модели, параметры и ограничения. Задачи математического программирования, классификация.
- •69.1Аналого-цифровые преобразователи.
- •70.1Цифро-аналоговые преобразователи.
- •70.2 Логические единицы работы многозадачных операционных систем и их использование
- •71.1Источники опорного напряжения и тока.
- •Ион на полевых транзисторах
- •72.3 Общие положения стандарта шифрования данных гост 28147-89 и режим простой замены в стандарте шифрования данных гост 28147-89.
- •73.1 Принципы конвейерной обработки информации в эвм.
- •73.2. Способы адресации и их использование в ассемблерных программах.
- •2. Непосредственная адресация
- •73.3 Понятие политики безопасности: общие положения, аксиомы защищённых систем, понятия доступа и монитора безопасности.
- •1 Человек-пользователь воспринимает объекты и получает информацию о состоянии ас через те субъекты, которыми он управляет и которые отображают информацию.
- •2 Угрозы компонентам ас исходят от субъекта, как активного компонента, изменяющего состояние объектов в ас.
- •3 Субъекты могут влиять друг на друга через изменяемые ими объекты, связанные с другими субъектами, порождая субъекты, представляющие угрозу для безопасности информации или работоспособности системы.
- •74.1Организация памяти эвм. Горизонтальное и вертикальное разбиение. Расслоение обращений. Организация памяти эвм. Горизонтальное и вертикальное разбиение памяти. Расслоение обращений.
- •74.2 Сравнение программных возможностей современных операционных систем ( Windows, Unix).
- •По удобству использования и наличию особых режимов
- •Вопрос 1
- •Вопрос 2
- •Понятие энтропии Энтропия как мера неопределенности
- •Свойства энтропии
- •75.1 Подходы к организации эвм. Эвм, управляемые данными. Эвм, управляемые запросами.
- •Методика построения помехоустойчивых кодов. Информационный предел избыточности
- •1.1. Принципы помехоустойчивого кодирования
- •761 Организация ввода-вывода информации в эвм. Программный обмен, обмен через прерывания, режим прямого доступа к памяти.
- •Организация ввода/вывода информации в эвм. Программный обмен, обмен через прерывания, режим прямого доступа к памяти.
- •Глава II
- •11.1. Проблемы организации систем ввода-вывода
- •11.2. Прямой доступ к памяти
- •9.16. Принципы организации системы прерывания программ.
- •76.2 Динамические структуры данных. Основные виды, способы построения.
- •76.3 Системный анализ, определение и этапы. Сущность системного подхода и его применение при проектировании асоиу.
- •2 Системный анализ. Определение и этапы.
- •77.1 История развития и современное состояние в области микропроцессорных систем.
- •77.2 Стандартные и структурированные типы данных.
- •77.3 Математическое описание объектов управления. Цель и задача управления. Принцип отрицательной обратной связи.
- •2.1. Математические методы построения оптимальных и адаптивных систем управления
- •2.1.1. Математическое описание объектов управления
- •2.1.2. Цель и задача управления
- •2.1.3. Задача оптимального управления и критерии качества
- •78.1 (Он же 80.1) Организация микроЭвм на базе микропрограммируемого микропроцессорного комплекта, типовые циклы функционирования.
- •78.2 Жизненный цикл программных средств. Этапы разработки программного обеспечения.
- •Программное обеспечение
- •Прог. Комплекс Документы
- •78. 3 Критерий качества. Методы решения задач оптимального управления
- •79.2 Нисходящее проектирование алгоритмов на примере моделирования арифметических операций сложения, вычитания, с плавающей запятой.
- •79.3 Понятия управляемости, достижимости и наблюдаемости динамических систем.
- •80.1 Организация микроЭвм на базе микропрограммируемого микропроцессорного комплекта, типовые циклы функционирования.
- •80.2 Восходящий метод проектирования алгоритмов и программ. Спроектировать схему универсального алгоритма перевода чисел из любой системы счисления в любую другую.
- •80.3 Методология структурного проектирования sadt.
62.1 Законы Кирхгофа и преобразование электрических цепей на их основе.
Законы Кирхгофа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Законы Кирхгофа являются основными в теории цепей.
Первый закон – закон токов Кирхгофа (ЗТК) формулируется по отношению к узлам электрической цепи и отражает тот факт, что в узлах не могут накапливаться заряды. Он гласит: алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю.
![]() ,
,
где m – число ветвей, сходящихся в узле.
В этом уравнении токи, одинаково ориентированные относительно узла, имеют одинаковые знаки. Например, знаки выходящих токов можно считать положительными, а входящих – отрицательными.
Число независимых уравнений, составляемых по ЗТК, равно числу независимых узлов электрической цепи.
Второй закон – закон напряжений Кирхгофа (ЗНК) формулируется по отношению к контурам и гласит: алгебраическая сумма напряжении ветвей в любом контуре цепи равна нулю.
![]() ,
,
где n – число ветвей, входящих в контур.
В этом уравнении напряжения, совпадающие с направлением обхода контура, записываются со знаком «+», а не совпадающие – со знаком «–».
Рассмотрим пример, в котором рассчитываются токи ветвей схемы резистивной цепи, изображенной на рисунке 2.1, по методу уравнений Кирхгофа. Схема имеет nу = 4 узла, nв = 6 ветвей. Выберем узел 4 в качестве базисного и составим nу - 1 = 3 уравнения по ЗТК: для 1-го узла -i1 + i3 + i4 = 0; для 2-го узла -i2 - i3 + i5 = 0; для 3-го узла i2 - i4 + i6 = 0. По ЗНК составляем nв - nу + 1 = 3 уравнения для контуров, показанных на рисунке стрелками: для 1-го контура -uг1 + u1 + u3 + u5 = 0; для 2-го контура uг2 + u2 - u3 + u4 = 0; для 3-го контура -uг2 - u2 + u6 - u5 = 0. Или с учетом закона Ома:
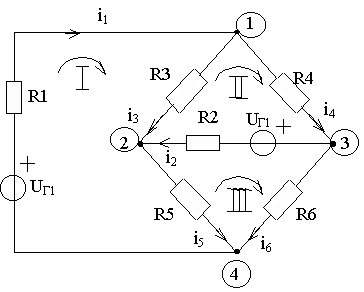
Рисунок 2.1 – Схема, отражающая применение ЗТК и ЗНК
-uг1 +R1i1 + R3i3 + R5i5 = 0 ;
uг2 + R2i2 - R3i3 + R4i4 = 0 ;
-uг2 -R2i2 + R6i6 - R5i5 = 0 .
Решая совместно эти системы уравнений, находят искомые токи.
Преобразование электрических схем
Преобразования электрических схем применяются для упрощения расчетов. Наиболее типичные методы преобразования следующие.
Последовательное соединение элементов. Согласно ЗТК при последовательном соединении элементов через них протекает один и тот же ток (рисунок 2.2).
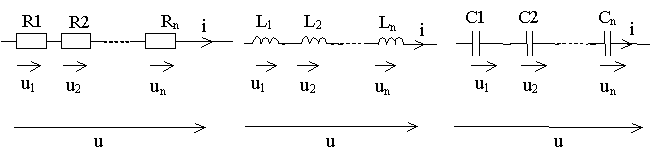
Согласно ЗНК напряжение, приложенное ко всей цепи:
![]()
Тогда для последовательного соединения резистивных элементов R1, R2, ..., Rn будем иметь:
![]() .
.
Для последовательного соединения индуктивных элементов:
![]() .
.
Для последовательного соединения емкостных элементов:
![]() .
.
При n = 2:
С = С1C2/(С1 + С2).
Таким образом, цепь из n последовательно соединенных резистивных, индуктивных или емкостных элементов может быть заменена одним эквивалентным резистивным, индуктивным или емкостным элементом.
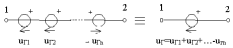
При последовательном соединении независимых источников напряжения, они заменяются одним эквивалентным источником напряжения с задающим напряжением uг, равным алгебраической сумме задающих напряжений отдельных источников. Причем со знаком «+» берутся задающие напряжения совпадающие с задающим напряжением эквивалентного источника, а со знаком «–» – несовпадающие.
Параллельное соединение элементов. При параллельном соединении элементов согласно ЗНК к ним будет приложено одно и то же напряжение.

Согласно ЗТК для тока каждой из схем, изображенных на рисунке выше, можно записать:
![]() .
.
На основании этого уравнения для параллельного соединения резистивных элементов получаем:
![]() .
.
Для параллельного соединения емкостных элементов:
![]() .
.
Для параллельного соединения индуктивных элементов:
![]() .
.
При n = 2:
R = R1R2/(R1 + R2); L = L1L2/(L1 + L2) .
Следовательно, цепь из n параллельно соединенных резистивных, индуктивных или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом.
Параллельно соединенные независимые источники тока можно заменить одним эквивалентным источником тока с задающим током, равным алгебраической сумме задающих токов отдельных источников. Причем со знаком «+» берутся задающие токи, совпадающие по направлению с задающим током эквивалентного источника, а со знаком «–» – не совпадающие.
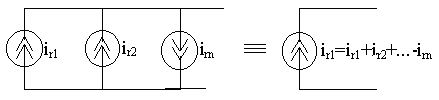
При расчете электрических цепей часто возникает необходимость преобразования источника напряжения с параметрами uг и Rг, в эквивалентный источник тока с параметрами iг и Gг, или наоборот – преобразование источника тока в эквивалентный источник напряжения. Эти преобразования осуществляются в соответствии с формулами:
iг = uг/Rг ; Gг = 1/Rг
Пример преобразования “звезда—треугольник”. Кроме последовательного и параллельного соединений элементов весьма распространенными являются соединения элементов треугольником и звездой.
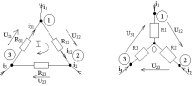
Существуют формулы преобразования соединения треугольника в звезду:
![]() ;
;
![]() ;
;![]() .
.
Обратный переход можно получить по формулам, которые получены из предыдущих:
R12 = R1 + R2 + R1R2/R3 ; R23 = R2 + R3 + R2R3/R1 ; R31 = R3 + R1 + R3R1/R2
62.2 Структура канала связи. Какие его компоненты наиболее сильно влияют на качественные характеристики тракта передачи данных. Что необходимо знать о канале связи при его использовании в сети передачи данных.
|
Канал связи – это совокупность технических и программных средств обеспечивающих передачу сообщения от источника к потребителю. Классификация каналов связи: 1. По назначению - телефонные - телеграфные - телевизионные - радиовещательные 2. По направлению передачи - симплексные (передача только в одном направлении) - полудуплексные (передача поочередно в обоих направлениях) - дуплексные (передача одновременно в обоих направлениях) 3. По характеру линии связи - механические - гидравлические - акустические - электрические (проводные) - радио (беспроводные) - оптические 4. По характеру сигналов на входе и выходе канала связи - аналоговые (непрерывные) - дискретные по времени - дискретные по уровню сигнала - цифровые (дискретные и по времени и по уровню) 5. По числу каналов на одну линию связи - одноканальные - многоканальные
Структура канала связи
ИС - источник сообщения ПС - получатель сообщения Т – передатчик (transmitter) R- приемник (reciever) ЛС - линия связи ИП - источник помех ЛС (тракт) – физическая среда, по которой распространяется сигнал от передатчика к приемнику S(t) – исходное сообщение X(t) – сообщение подготовленное передатчиком и переданное по линии связи x(t) – сообщение, принятое приемником s(t) – сообщение, восстановленное приемником для получателя сообщения. В связи с тем, что на канал связи действуют различные помехи – X(t) не равно x(t) и S(t) не равно s(t) Характеристики качества каналов и трактов связи Основным видом каналов связи является стандартный канал тональной частоты КТЧ. Качество таких каналов определяется следующими основными параметрами и характеристиками: - шумовой защищённостью каналов аш [дБ]; - достоверностью передачи дискретных сообщений Q; - надёжностью линии связи по замираниям Н [%]; -характеристиками канала ТЧ: остаточным затуханием, амплитудной, амлитудно-частотной, фазочастотной;
Нормы на эти параметры и характеристики указываются в технических условиях для конкретных образцов систем связи.
Характеристики Канал связи характеризуется ёмкостью (объёмом) Vk[1], который определяется по формуле: Vk = TkFkDk, где Tk — время возможной передачи информации через канал; Fk — полоса пропускания канала; Dk — динамический диапазон канала: Dk = Ps / Pi, где Ps — допустимая в канале мощность передаваемого сигнала, а Pi — мощность помехи в канале. |
62.3 Оценка точности и достоверности результатов статистического моделирования (планирование эксперимента). Методы понижения дисперсии: ускоренный расчет интегралов; метод существенной выборки, метод стратифицированной выборки.
Планирование статистического эксперимента
Пусть X = (x1 , ... ,xk) - вектор случайных величин, имеющий распределение PX. Во многих случаях цель статистического эксперимента может быть сведена к определению математического ожидания с.в. y = g(X), где g(x) - заданная функция с.в. X. Поэтому типовая схема статистического эксперимента имеет вид рис.
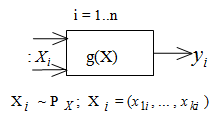
Здесь
оценка
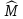 y
приближается к точному значению My с
ростом числа опытов n.
y
приближается к точному значению My с
ростом числа опытов n.
1. Прямая задача планирования: известно число опытов, требуется определить погрешность M;^y.
Оценка M;^y является случайной величиной, т.к. представляет cобой функцию от случайных величин:
M;^y
=
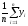
В типовой схеме статистического эксперимента используются независимые реализации xi, поэтому с.в. yi в формуле также независимы. Из центральной предельной теоремы вытекает, что с.в. M;^y при больших n имеет нормальное распределение, т.е. M;^y ~ N[m,]. Определим параметры этого распределения:
m
= M(M;^y) = M( )
=
)
=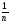 M(
M( )
=
)
=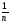
 M(
M(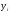 )
=
)
=
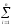 My
= My
My
= My
σ2
= D(M;^y) = D(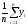 )
=
)
= D(
D(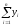 )
=
)
=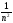
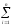 D(
D(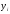 )
=
)
=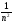
 Dy
=
Dy
=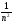 n
Dy
=
n
Dy
=
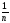 Dy
Dy

Таким
образом, при увеличении числа опытов
на порядок
уменьшается в
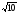
 3
раза. На рис. схематически показан вид
распределения оценки M;^ в зависимости
от n.
3
раза. На рис. схематически показан вид
распределения оценки M;^ в зависимости
от n.
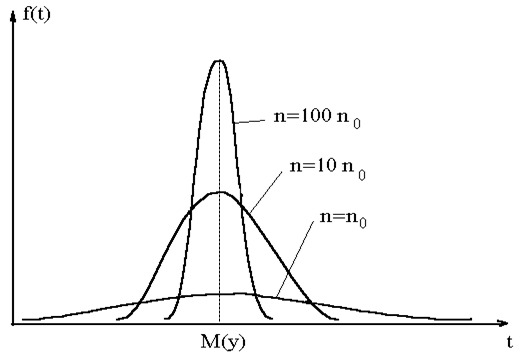
Диапазон
вероятных отклонений оценки от точного
значения M(y) сужается пропорционально
 .
Параметр
используют как показатель точности
оценки. Поскольку M;^y имеет нормальное
распределение, то практически достоверно,
что M;^y отклоняется от искомого M;^(y)
не более, чем на 3.
Можно сказать, что
является аналогом абсолютной погрешности,
а 3
- самой абсолютной погрешностью.
.
Параметр
используют как показатель точности
оценки. Поскольку M;^y имеет нормальное
распределение, то практически достоверно,
что M;^y отклоняется от искомого M;^(y)
не более, чем на 3.
Можно сказать, что
является аналогом абсолютной погрешности,
а 3
- самой абсолютной погрешностью.
2. Обратная задача планирования: известна погрешность 3(M;^y), надо найти число опытов n.
∆ =
3(M;^y)
=
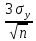 =
=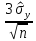 (с.к.о. неизвестна, поэтому берём её
оценку).
(с.к.о. неизвестна, поэтому берём её
оценку).
 =
=
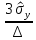
n
= ( )2
)2
Понижение дисперсии
Под аналитико-статистическим подходом будем понимать изобретение всевозможных усовершенствований схемы статистического эксперимента с целью уменьшить число опытов N, необходимое для достижения заданной точности расчетов.
При этом усовершенствования схемы эксперимента выполняются путем ее формального, т.е. аналитического преобразования. Сам же эксперимент остается статистическим.
Идея понижения дисперсии. Она состоит в следующем.
Поскольку при заданной точности v число опытов N определяется формулой
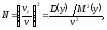
то
N можно уменьшить за счет снижения
дисперсии D(y) выходной с.в. y. Точнее
говоря, вместо y предлагается разыгрывать
"немножко другую" с.в.
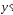 с тем же значением искомого м.о. M(
с тем же значением искомого м.о. M( )
= M(y), но с меньшей дисперсией D(
)
= M(y), но с меньшей дисперсией D(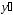 )
<< D(y).
)
<< D(y).
Расчёт интегралов
I
= h(t)dt =
h(t)dt =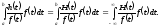
H(t)
= h(t), при
t (a,b)
(a,b)
H(t) = 0, в противном случае.
От выбора функции f(t) зависит скорость сходимости оценки I' к точному значению интеграла I.
Скорость сходимости I' к I определяется главным образом дисперсией с.в. y = H(x)/f(x). Чем меньше D(y), тем скорее сходится статистическое среднее I'= = (y1 + ... + yn )/n.
Поэтому рекомендуется подбирать f(t) так, чтобы с.в. H(x)/f(x) была по возможности ближе к константе, т.к. при y = const было бы D(y) = 0. Но H(x)/f(x) = const означает, что f(x) = const H(x). Следовательно, нужно стремиться, чтобы функция f была "подобна" функции H.
Метод взвешивания
Для простоты изложения метода рассмотрим статистический эксперимент с одномерной входной с.в. x (рис. 6.1).
x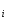 ~
f(t) i = 1..N
~
f(t) i = 1..N
y(x)
y M;^y
M;^y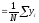



Рис. 6.1. Исходная схема эксперимента
Формально искомое м.о. M(y) определяется выражением:
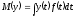 (6.1)
(6.1)
Метод взвешивания основан на аналитическом преобразовании выражения (6.1) и на соответствующем изменении схемы эксперимента.
Разделим и умножим подынтегральное выражение в (6.1) на произвольную п.р.в. p(t), не равную нулю в пределах интегрирования. В результате мы увидим, что
 (6.2)
(6.2)
где
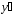 = y(x) f(x) / p(x), а x ~ p(t). Следовательно,
вместо расчета оценки M;^ можно выполнять
расчет оценки M;^y'.
Схема расчетаM;^y'
представлена на рис. 6.2. Такой переход
от исходной схемы рис. 6.1 к схеме рис.
6.2 называется методом взвешивания. Обе
схемы эквивалентны с точки зрения м.о.
выходной с.в., но различны с точки зрения
ее дисперсии.
= y(x) f(x) / p(x), а x ~ p(t). Следовательно,
вместо расчета оценки M;^ можно выполнять
расчет оценки M;^y'.
Схема расчетаM;^y'
представлена на рис. 6.2. Такой переход
от исходной схемы рис. 6.1 к схеме рис.
6.2 называется методом взвешивания. Обе
схемы эквивалентны с точки зрения м.о.
выходной с.в., но различны с точки зрения
ее дисперсии.
i = 1..N Перемножение
x ~
p(t)
y
~
p(t)
y



y(x)
*





f(x)/p(x)
M;^y'


Рис. 6. 2. Преобразованная схема
Описанный
одномерный вариант метода легко
распространяется и на случай многомерной
с.в. Для этого достаточно в (6.2) вместо
скаляров x,t записать соответственно
векторы X = (x ,
... , x
,
... , x ),
T = (t
),
T = (t ,
... , t
,
... , t ). Обобщение на случай дискретной с.в.
X осуществляется путем замены интеграла
на сумму, а плотностей - на вероятности.
). Обобщение на случай дискретной с.в.
X осуществляется путем замены интеграла
на сумму, а плотностей - на вероятности.
Искусство
применения метода взвешивания сводится
к подбору такой функции p, чтобы было
D(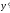 )
<< D(y). Тогда получится N' << N. Можно,
например, подбирать п.р.в. p так, чтобы
с.в.
)
<< D(y). Тогда получится N' << N. Можно,
например, подбирать п.р.в. p так, чтобы
с.в.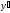 =
y f / p была по возможности ближе к
константе, хотя бы в каком-нибудь
интуитивном смысле, т.к. при
=
y f / p была по возможности ближе к
константе, хотя бы в каком-нибудь
интуитивном смысле, т.к. при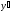 = =const должно быть D(
= =const должно быть D(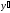 )
= 0.
)
= 0.
Основное достоинство метода взвешивания - в простоте преобразования схемы эксперимента. Программа вычисления функции y(x), т.е. модель исследуемой системы не меняется. Добавляется только расчет множителя f/p (веса), да генератор входной с.в. с распределением f заменяется на генератор с распределением p.
Метод расслоения
Необходимо
рассчитать надёжность неприводимой
системы при малых (и одинаковых)
вероятностях отказа элементов: pk =
p = 2·10–4
(k = 1, …, 7).
Поскольку система отказывает только
при одновременном отказе минимум двух
элементов, то вероятность Q
отказа системы имеет порядок величины
p2,
и поэтому для вычисления оценки
 придётся проводить опыты, число которых
составляет сотни миллионов.
придётся проводить опыты, число которых
составляет сотни миллионов.
Чтобы сократить необходимое число опытов, усовершенствуем схему статистического эксперимента. В соответствии с методом расслоения рассмотрим множество всех возможных значений входной с.в. Х.
В исходном (непосредственном) статистическом эксперименте входная с.в. Х определяется в виде
Х = (x1, ..., x7), (2.34)
где компоненты x1, ..., x7 {0, 1} обозначают состояния элементов системы (0 – элемент работает, 1 – элемент отказал). Вероятности отказа элементов известны: Р{xk = 1} = 2∙10–4. Выходная с.в. (состояние системы) y {0, 1} является определённой функцией от с.в. Х: y = y(Х). Искомая вероятность отказа системы Q = Р{y = 1} = M(y). Для входной с.в. Х пространство возможных исходов состоит из 27 = 128 значений двоичного вектора Х:
= {(0000000), (0000001), ..., (1111110), (1111111)}. (2.35)
Чтобы выполнить эффективное расслоение эксперимента, слой j определим как подмножество таких значений с.в. Х, которые содержат ровно j единиц. Определяемый таким образом слой j содержит те исходы, в которых отказывают ровно j элементов системы (j = 0, 1, ..., 7). Искомое м.о. М(у) выходной с.в. у можно выразить через условные м.о. следующим образом:
M(y) = w0M0 + w1M1 + ... + w7M7, (2.36)
где Мj = М(y|X j) – условное м.о. величины у (т. е. условная вероятность отказа системы) в слое j; wj – вероятность слоя j (т. е. вероятность того, что в системе откажут ровно j элементов).
Формула (2.36) определяет общую схему разделения исходного статистического эксперимента на эксперименты в отдельных слоях j. Рассматривая слагаемые в правой части формулы (2.36) по отдельности, её можно существенно упростить.
Из надёжностных графов системы (табл. 2.5) видно, что система может отказать только тогда, когда откажут два или более элементов. Поэтому в формуле (2.36) заведомо М0 = 0 (вероятность отказа системы при условии, что отказало 0 элементов, равна нулю) и М1 = 0 (вероятность отказа системы при условии, что отказал ровно 1 элемент, тоже равна нулю). С учётом этого соотношение (2.36) принимает вид:
M(y) = w2M2 + ... + w7M7. (2.37)
Вычислим для выражения (2.37) вероятности с w2 по w4:
w2 = Р{2} = 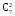 p2(1–p)5 = 21.0,00022.0,99985 = 8,3916.10–7;
p2(1–p)5 = 21.0,00022.0,99985 = 8,3916.10–7;
w3 = Р{3} = 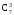 p3(1–p)4 = 35.0,00023.0,99984 = 2,7977.10–10; (2.38)
p3(1–p)4 = 35.0,00023.0,99984 = 2,7977.10–10; (2.38)
w4 = Р{4} = 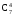 p4(1–p)3 = 35.0,00024.0,99983 = 5,5966.10–14.
p4(1–p)3 = 35.0,00024.0,99983 = 5,5966.10–14.
Вероятности wj быстро убывают с номером слоя j, поэтому в правой части соотношения (2.37) можно, видимо, всеми слагаемыми, кроме двух-трёх первых, пренебречь. Чтобы уточнить это предположение, найдём ещё (для первого слагаемого) грубую оценку условной вероятности M2.
Учитывая,
что в системе имеются два критических
элемента, при одновременном отказе
которых система обязательно откажет,
заключаем: вероятность M2
(условная) отказа системы не может быть
меньше вероятности 1/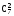 0,05
(условной) того, что откажет именноэтапара
критических элементов. Таким образом:
0,05
(условной) того, что откажет именноэтапара
критических элементов. Таким образом:
M2 0,05; w2M2 0,05w2 4,2.10-8. (2.39)
Отсюда видно, что слагаемое w2M2 в выражении (2.37) превосходит величину слагаемого w4M4 (даже если M4 = 1) примерно в миллион раз. Очевидно также, что слагаемые w5M5, ..., w7M7 еще менее значимы и, следовательно, выражение (2.37) можно переписать в виде практически точного равенства:
M(y) =w2M2 + w3M3 , (2.40)
в котором, кстати, второе слагаемое тоже, как минимум, в сто раз меньше первого.
Заменяя
в равенстве (2.40) математические ожидания
их статистическими оценками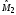 и
и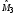 ,
получаем следующую формулу для расчёта
вероятности отказа системы через её
условные вероятности отказа в слоях2
и 3:
,
получаем следующую формулу для расчёта
вероятности отказа системы через её
условные вероятности отказа в слоях2
и 3:
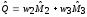 . (2.41)
. (2.41)
Это основная формула расслоенного эксперимента для нашей системы.
Из проведённого расчёта можно сделать общий вывод, что чем надёжнее элементы системы, тем быстрее убывают вероятности слоёв в формулах (2.38), тем меньше остаётся слоёв в выражении (2.37) и, следовательно, тем меньше их остаётся в формуле расслоенного эксперимента (2.41). Тем самым высокая надёжность системы – причина, усложняющая применение непосредственного статистического моделирования – становится фактором, повышающим эффективность метода расслоения.