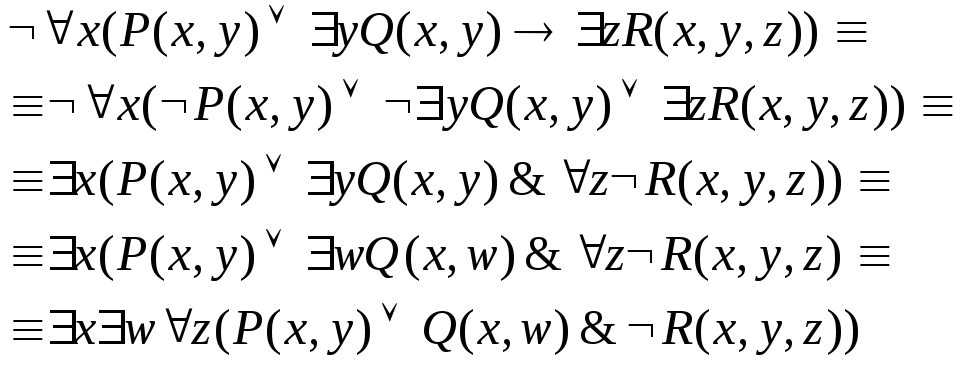3.5. Приведенная форма представления предикатов

Формула, в которой из логических символов встречаются только ⌐, &, , причем отрицание должно стоять перед символами предикатов, называется приведенной формой.

Приведенная форма называется нормальной(ПНФ), если она не содержит символов кванторов или все символы кванторов стоят в начале формулы за скобками (кванторная приставка).

Алгоритм построения ПНФ

1. Исключить связки →, ~ с помощью законов преобразования логики предикатов.

2. Перенести знак ⌐ внутрь формулы.

3. Если нужно переименовать связанные переменные.

4. Используя законы преобразования логики предикатов перейти к КНФ.

Пример.

	Исключаем импликацию
	Переносим знак ⌐ внутрь формулы
	Переименовываем связанные переменные.

Чтобы избавиться от кванторов применяют процедуру сколемизации (от фамилии математика Skolem). Сколемизация позволяет получить запись предикатов, не содержащих свободных переменных в форме без кванторов.

. Чтобы выполнить сколемизацию надо:

1. Отбросить кванторы существования для чего

• если левее нет кванторов общности, то соответствующая переменная заменяется на константу Сколема (а_с);

• иначе переменная заменяется функцией Сколема (fc) от переменных, на которые навешаны кванторы общности, стоящие левее данного квантора существования.

2. Отбросить кванторы общности.

Пример :

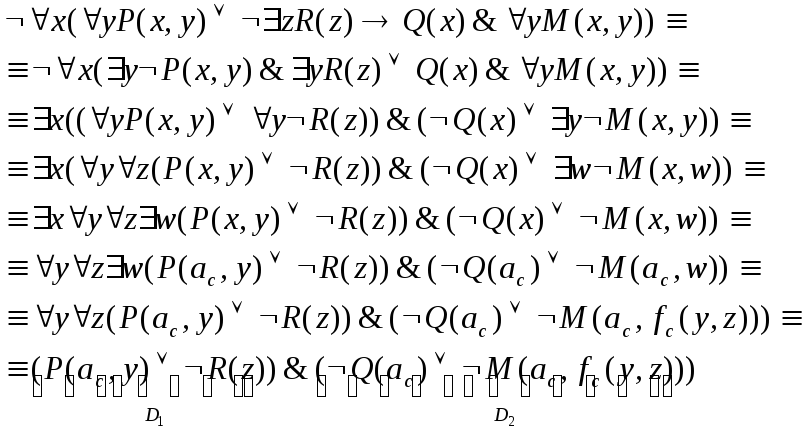
Тема 4. Автоматическое доказательство теорем

Автоматическое доказательство теорем – это основа логического программирования. Классическим методом АТД является метод резолюции.

4.1. Постановка задачи

Алгоритм, который проверяет отношение для формулыS, множества формул Г и теорииназывается алгоритмом автоматического доказательства теорем (АТД).

В общем случае такой алгоритм невозможен, т. е. не существует алгоритма, который для любых S, Г ивыдавал бы ответ «ДА», если Г |-Sи «НЕТ» в противном случае. Но в некоторых случаях можно построить алгоритм, который применим не ко всем формулам теории (т. е. частичный алгоритм). Для некоторых простых формальных теорий (например, теории высказываний) алгоритмы АТД известны.

Пример.Для исчисления высказываний известно, что теоремами являются тавтологии, т. е. можно проверить является ли формула тавтологией с помощью таблиц истинности. Этот пример является примером доказательства теорем в теории £, но не является алгоритмом автоматического поиска вывода теорем из аксиоматической теории £.

Наиболее известный классический алгоритм АТД называется методом резолюций (МР). Для любого прикладного исчисления предикатов 1 порядка он дает ответ «ДА», если Г |- Sи «НЕТ» или не выдает ответа в противном случае.

4.2. Доказательство от противного

В основе МР лежит идея доказательства от противного.

Теорема.Если, гдеFпротиворечие, то Г |-S.

Доказательство (для теории £).

1. По теореме дедукции, если Г – множество формул, А и BГ иA|-_£B, то Г|-А→В.

2. , следовательно.

3. Следствие из теоремы дедукции: А |- B, то |-AB.

4. Из 2 и 3 получаем . Т.к.F– противоречие, т. е.F=0, то

5. По теореме дедукции ГS, следовательно, Г|-S.

Пустая формула не является истинной или ложной ни в какой интерпретации и, по определению, является противоречием. В качестве формулы Fпри доказательстве от противного по МР принято использовать пустую формулу ().

МР работает с особой стандартной формой формул, которая называется предложением или дизъюнктом.

Дизъюнкт - безкванторная ДНФ.