
ВМ26
.pdf
13. Интегрирование тригонометрических и иррациональных выражений
Интегралы вида |
|
|
вычисляются с помощью универсальной тригономет- |
|
рической подстановки |
t = tg |
x |
. Этой подстановкой интеграл преобразуется в интеграл |
|
2 |
||||
|
|
|
от рациональной функции переменной t.
Иногда ее использование приводит к интегрированию громоздких рациональных дробей. Поэтому в ряде случаев более удачно используют частные подстановки:
1)если подынтегральная функция нечетна относительно sin x, то подстановка t = cos x,
2)если подынтегральная функция нечетна относительно cos x, то подстановка t = sin x,
3)если подынтегральная функция четная относительно sin x и cos x,то подстановка t = tg x.
При вычислении интегралов вида |
∫sinn x cosm xdx (m,n Z; m ≥ 0; n ≥ 0) используем |
следующие правила: |
|
1)если хотя бы одно из чисел m или n нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin2 x + cos2 x = 1, оставшуюся четную степень через кофункцию, приходим к табличному интегралу,
2)если же m и n – четные неотрицательные числа, то степени понижаются посредством перехода к двойному аргументу с помощью тригонометрических формул:
3)если m и n – четные и хотя бы один из них отрицательный, то замена tg x = t. Интегралывида ∫sin mx cosnxdx вычисляютсяпутемразложенияподынтегральнойфункции
на слагаемые по формулам: 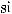
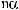
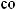
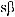

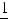
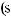
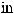
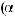
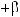
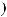

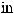
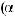

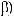
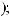
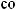
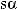
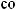
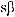


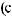
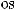
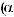
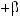
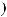
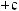

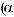


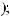

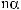
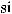
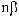


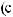
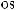
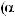

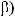

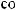
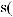
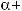
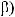
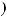 .
.
Интегралы вида 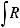
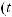
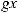
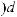
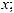
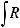

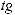
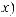
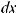 можно найти с помощью замены tgx = t; ctgx = t. Подынтегральное выражение в полученных интегралах будет рациональной функцией от t.
можно найти с помощью замены tgx = t; ctgx = t. Подынтегральное выражение в полученных интегралах будет рациональной функцией от t.
Интегралы вида ∫R(x; n1 xm1 ; n2 xm2 ...)dx(m,n Z ) вычисляются подстановкой x = ts, где s – общий знаменатель дробей
xm2 ...)dx(m,n Z ) вычисляются подстановкой x = ts, где s – общий знаменатель дробей 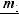


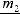

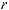

 , т.е. интеграл приводится к рациональной
, т.е. интеграл приводится к рациональной
функции от переменной t: 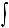
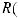
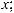

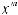



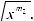

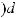
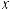

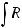
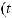

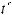

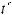


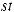
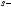
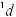
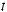 .
.
При вычислении интегралов вида |
|
|
|
|
|
исполь- |
||
|
|
|
||||||
зуют подстановкой |
ax +b |
= t s , где s – общий знаменатель дробей |
m1 |
; m2 .... |
||||
|
cx +d |
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
1 |
2 |
Интегралы вида |
|
|
|
|
|
|
|
вычисляются |
путем выделением полного квадрата в подкоренном выражении и соответствующей подстановки.
30

Для вычисления интегралов вида |
применяют следующие правила: |
а) квадратный трехчлен ax2 + bx + c путем выделения полного квадрата и замены переменной может быть представлен в виде u2 ± k2. Таким образом, интеграл будет сведен к одному
из интегралов: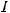

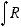
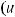


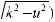
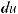

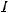

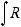



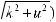


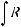
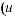


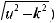
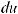 .
.
б) интеграл I1 подстановкой u = ksint (u = kcost) сводится к интегралу от рациональной функции относительно sint и cost.
u = ksint (k > 0) → du = kcostdt → 
 k 2 −u2 = k cos t;
k 2 −u2 = k cos t; 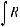
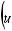


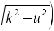
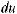

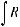
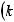
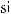

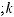
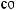
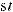
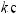
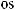
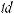
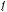 .
.
Аналогично интегралы I2 и I3 подстановками подстановкой u = ktgt (u = kctgt) и u = |
|
k |
|||||||||||||||||||
|
cost |
||||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
соответственно сводятся к интегралам от рациональной функции относительно |
|||||||||||||||||||||
u = |
|
|
|||||||||||||||||||
|
|||||||||||||||||||||
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sint и cost. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интегралы вида 
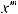
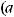
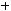
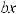

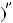
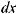 (m, n, p, a, b – рациональные числа) называются интег-
(m, n, p, a, b – рациональные числа) называются интег-
ралами от дифференциального бинома 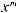
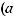
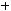
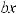

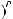 . Они выражаются через элементарные функции только в следующих трех случаях:
. Они выражаются через элементарные функции только в следующих трех случаях:
1)если p Z, то u = ts, где S – знаменатель дробей m и n;
2)если mn+1 Z, то a + bxn = ts, где S – знаменатель дроби p = Sk ;
3)если mn+1 + p Z, то ax-n + b= ts, где S – знаменатель дроби p = Sk .
Во всех остальных случаях интегралы от дифференциального бинома не выражаются через элементарные функции.
Вычислите интегралы: |
|
Задачи |
|
|
|
13.1. |
13.2. |
13.3. |
13.4. |
13.5. |
13.6. |
13.7. |
13.8. |
13.9. |
13.10. |
13.11. |
13.12. |
13.13. |
13.14. |
13.15. |
13.16. |
13.17. |
13.18. |
13.19. |
13.20. |
13.21. |
13.22. |
13.23. |
13.24. |
|
|
31 |
14. Определенный интеграл. Методы вычисления определенного интеграла
Пустьнаотрезке[a;b] определенафункцияf (x).Разобьемотрезок[a;b] наn частейточками a = x0 < x1 < x2 < ... < xn = b. Из каждого интервала [xi-1; xi] возьмем произвольную точку ζi
и составим сумму |
где xi = xi – xi-1. Полученная сумма называется интегральной |
суммой,аеепределприmax |
xi →0,еслионсуществуетиконечен,называетсяопределенным |
интегралом от функции f (x) в пределах от a до b и обозначается:
Функция f (x) в этом случае называется интегрируемой на отрезке [a;b].
Если функция f (x) непрерывна на [a;b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [a;b] на элементарные отрезки и от выбора точек ζi. Числа a и b соответственно называются нижним и верхним пределами интегрирования.
Простейшие свойства определенного интеграла
1. |
|
|
. |
|
|
|
|
|
|
|
|||
2. |
. |
|
|
|
||
3. |
|
|
, где |
|||
4. |
|
|
|
. |
|
|
5. |
|
|
, где C – постоянная. |
|||
|
|
|
Правила вычисления определенного интеграла |
|||
1. |
Формула Ньютона-Лейбница: ∫b |
f (x)dx = F(x) |
|
ba = F(b)− F(a),где F (x) – первообразная |
||
|
||||||
|
|
|||||
|
|
|
a |
|
|
|
для функции f (x) т.е. F' (x) = f (x).
b b
2. Интегрирование по частям: ∫udv = uv ba −∫vdu, где u = u(x) v = v(x) – непрерывно диф-
a a
ференцируемые функции на отрезке [a;b].
bβ
3.Замена переменной: ∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt, где φ (t) – функция, непрерывная вместе
aα
со своей производной φ' (t) на отрезке α ≤ t ≤ β (a = φ(α) b = φ(β)), f (φ(t)) – функция непрерывная на [α;β].
4.Если f (x) – нечетная функция, т.е. f (-x) = -f (x) то ∫a f (x)dx = 0.
−a
5.Если f (x) – четная функция, т.е. f (-x) = -f (x) то ∫a f (x)dx = 2∫a f (x)dx.
−a 0
32

Задачи
Вычислите интегралы: |
|
|
|
|
14.1. |
14.2. |
14.3. |
14.4. |
|
14.5. |
14.6. |
14.7. |
14.8. |
|
14.9. |
14.10. |
14.11. |
14.12. |
|
14.13. |
14.14. |
14.15. |
14.16. |
|
14.17. |
14.18. |
14.19. |
14.20. |
|
14.21. |
14.22. |
14.23. |
14.24. |
|
14.25. |
14.26. |
14.27. |
14.28. |
|
14.29. |
14.30. |
14.31. |
14.32. |
|
14.33. |
14.34. |
14.35. |
14.36. |
|
14.37. |
14.38. |
14.39. |
14.40. |
. |
|
|
ОТВЕТЫ |
|
|
14.1. 19; 14.2. 20; 14.3. 21 |
8 |
; 14.4. |
|
|
; 14.5. 8 |
3 |
; 14.6. |
2 |
9 |
; 14.7. |
|
|
|
; 14.8. 4е; 14.9. 2; |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
−1 |
; 14.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
14.10. 0,25; 14.11. |
|
|
3 |
|
; 14.13. ln(1+ |
|
|
|
); 14.14. ln |
|
+3π |
|
; 14.15. 2; 14.16. 1 ; |
|||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
8 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
14.17. 1; 14.18. |
π |
12 |
; 14.19. 2е(е–1); 14.20. 0; 14.21. π3 |
|
; 14.22. 0,2; 14.23. 2 |
3 |
; 14.24. 0,4; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
192 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14.25. |
1−ln 2 |
; |
14.26. ln |
4 |
|
|
; |
14.27. |
0; 14.28. ln |
|
|
− π |
|
|
|
|
; |
|
14.29. 32 ; 14.30. |
2(1+ln 2); |
||||||||||||||||||||
3 |
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2e |
|
; 14.35. 2 In 2 – 1; 14.36. 4 −π ; |
||||||||||||||||||||||||||||
14.31.1,5(ln4 −1); 14.32. π |
3 |
− |
3 |
2 |
; 14.33. 2 – In 2; 14.34. ln |
|
|
|||||||||||||||||||||||||||||||||
|
e +1 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||
14.37. –2; 14.38.1− |
2; 14.39. 2 In 2 – 1; 14.40. 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
33

15. Несобственные интегралы
Несобственными интегралами называются интегралы с бесконечными пределами и интегралы от неограниченных функций.
Интегралы с бесконечными пределами
+∞∫ f (x)dx = alim→−∞ ∫c |
f (x)dx +blim→+∞ ∫b |
f (x)dx, где c (a;b). |
|
−∞ |
a |
c |
|
Интегралы от разрывных функций
Если функция f (x) имеет бесконечный разрыв в точке c отрезка [a;b] и непрерывна для всех остальных значений x [a;b], то по определению полагают:
∫b |
f (x)dx = limε→0 c∫−ε |
f (x)dx +limε→0 |
∫b |
f (x)dx. |
a |
a |
|
c+ε |
|
Если функция f (x) имеет разрыв при x = a, а во всех других точках отрезка [a;b] непрерывна,
то ∫b |
f (x)dx = limε→0 |
∫b |
f (x)dx. |
|
a |
|
a+ε |
|
|
Аналогично, если x = b – точка разрыва функции f (x), то ∫b |
f (x)dx = limε→0 b∫−ε f (x)dx. |
|||
|
|
|
a |
a |
Несобственный интеграл называется сходящимся, если определяющие его пределы существуют и конечны. Если же хотя бы один из пределов не существует или равен бесконечно-
сти, то интеграл расходится.
Задачи
Вычислите несобственные интегралы или доказать их расходимость:
15.1. |
|
|
|
|
|
|
|
|
|
|
15.2. |
|
|
|
|
|
15.3. |
|
|
|
|
|
|
|
|
|
|
|
15.4. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
15.5. |
|
|
|
|
|
|
|
|
|
|
15.6. |
|
|
|
15.7. |
|
|
|
|
|
|
|
|
|
|
|
15.8. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
15.9. |
|
|
|
|
|
|
|
|
|
|
15.10. |
|
|
|
|
15.11. |
|
|
|
|
|
|
|
|
|
|
|
15.12. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.13. |
|
|
|
|
|
|
|
|
|
|
15.14. |
|
|
|
15.15. |
|
|
|
|
|
|
|
|
|
|
|
15.16. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15.1.1; 15.2.расходится; 15.3.расходится; 15.4.1; 15.5.расходится; 15.6.-1; 15.7. 3 |
4 |
; 15.8.π; |
|||||||||||||||||||||||||||||||||||||||||
15.9. π; 15.10. расходится; 15.11. π; 15.12. 4; 15.13. 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
; 15.14. |
3(3 |
|
+1); 15.15. расходится; |
|||||||||||||||||||||||||||||||||||||
3 |
2 |
||||||||||||||||||||||||||||||||||||||||||
15.16. расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
34

16. Приложения определенного интеграла
Вычисление площади плоской фигуры
В прямоугольной системе координат площадь криволинейной трапеции, ограниченной кривой y = f (x) ( f (x) ≥ 0), прямыми x = a, x = b и осью OX, вычисляется по формуле:
S = ∫b f (x)dx.
a
Если f (x) < 0, то S = −∫b f (x)dx.
a
Площадь фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x) ( f1 (x) ≤ f2 (x)) и прямыми x = a, x = b, находится по формуле:
S = ∫b (f2 (x)− f1 (x))dx.
a
Площадь криволинейной трапеции, ограниченной кривой x = φ (y) (φ (y) ≥ 0), прямыми y = c, y = d и осью OY выражается формулой:
S = ∫d ϕ(y)dy.
c
Площадь фигуры, ограниченной кривыми x = φ1 (y) и x = φ2 (y) (φ1 (y) ≤ φ2 (y)) и прямыми y = c, y = d, находится по формуле:
S = ∫d (ϕ2 (y)−ϕ1 (y))dy.
c
Если кривая задана параметрически уравнениями x = x (t), y = y (t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x = a, x = b и осью OX, выражается формулой:
t2
S = ∫y(t)x'(t)dt,
t1
где t1 и t2 определяются из уравнений a = x (t1), b = x (t2) (y (t) ≥ 0 при t1 ≤ t ≤ t2). В полярной системе координат площадь криволинейного сектора, ограниченного кривой,
заданной уравнением ρ = ρ (φ) и двумя полярными радиусами φ = α, φ = β (α < β), находится по формуле:
S = 1 ∫β ρ2 dϕ.
2 α
Площадь фигуры, ограниченной кривыми ρ = ρ1 (φ) и ρ = ρ2 (φ) (ρ1 (φ) ≤ ρ2 (φ)) и двумя полярными радиусами φ = α, φ = β (α < β) выражается формулой:
S = |
1 |
∫β (ρ22 − ρ12 )dϕ. |
|
2 |
α |
Вычисление длины дуги плоской кривой
Если кривая задана в прямоугольной системе координат уравнением y = f (x), a ≤ x ≤ b, то длина дуги этой кривой вычисляется по формуле:
l = ∫b 
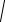 1+(y')2 dx.
1+(y')2 dx.
a
35

При параметрическом задании кривой x = x (t), y = y (t) (x = x (t), y = y (t) – непрерывнодифференцируемые функции) длина дуги кривой, соответствующая монотонному изменению параметра t от t1 до t2, находится по формуле:
t2
l = ∫
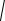 (x')2 +(y')2 dt.
(x')2 +(y')2 dt.
t1
Если кривая задана в полярных координатах уравнениемρ = ρ (φ),α ≤ φ ≤ β, то длина дуги равна:
β
l = ∫
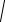 ρ2 +(ρ')2 dϕ.
ρ2 +(ρ')2 dϕ.
α
Вычисление объема тел
Если площадь сечения тела плоскостью, перпендикулярной оси OX, может быть выражена как функция от x, т.е. в виде S = S (x) (a ≤ x ≤ b), то объем части тела, заключенной между перпендикулярными оси OX плоскостями x = a и x = b, находятся по формуле:
V = ∫b S(x)dx .
a
Если криволинейная трапеция, ограниченная кривой y = f (x), прямыми x = a, x = b, y = 0, вращается вокруг оси OX, то объем тела вращения вычисляется по формуле:
V =π∫b y2dx.
a
Если фигура, ограниченная кривыми y = f1 (x) и y = f2 (x) (0 ≤ f1 (x) ≤ f2 (x)) и прямыми x = a, x = b, вращается вокруг оси OX, то объем тела вращения равен:
b
V =π∫(y22 − y12 )dx.
a
Если криволинейная трапеция, ограниченная кривой x = φ (y), прямыми x = 0, y = c, y = d вращается вокруг оси OY, объем тела вращения выражается формулой:
V =π ∫d x2dy.
c
Если фигура, ограниченная кривыми x = φ1 (y) и x = φ2 (y) (0 ≤ φ1 (y) ≤ φ2 (y)) и прямыми y = c, y = d, вращается вокруг оси OY, то объем тела вращения находится по формуле:
d
V =π∫(x22 − x12 )dy.
c
Вычисление площади поверхности вращения
Если дуга кривой y = f (x) (a ≤ x ≤ b), вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле:
S = 2π ∫b y
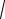 1+ (y')2 dx.
1+ (y')2 dx.
a
Если кривая задана параметрическими уравнениями x = x (t), y = y (t) (t1 ≤ t ≤ t2 ), то:
t2
S = 2π∫y
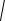 (x')2 +(y')2 dt.
(x')2 +(y')2 dt.
t1
Если кривая задана в полярных координатах уравнением ρ = ρ (φ) (α ≤ φ ≤ β), то:
β
S = 2π ∫ρ
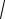 ρ2 + (ρ' )2 dϕ.
ρ2 + (ρ' )2 dϕ.
α
36

Задачи
Вычислите площадь фигуры, ограниченной линиями, заданными в прямоугольной системе координат:
16.1. |
|
|
|
|
|
16.2. |
16.3. |
|||||||||
|
|
|||||||||||||||
16.4. |
|
|
|
|
|
|
|
|
|
|
|
|
16.5. |
16.6. |
||
|
|
|
|
|
||||||||||||
16.7. |
|
|
|
|
|
|
16.8. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
16.9. |
|
|
|
16.10. |
|
|
||||||||||
Вычислите площадь фигуры, ограниченной кривыми, заданными в полярной системе координат:
16.11. |
16.12. |
|
|
|
|
16.13. |
||||
16.14. |
|
16.15. |
|
|
|
|
16.16. |
|||
|
||||||||||
Вычислите длину дуги плоской кривой: |
|
|
||||||||
16.17. |
16.18. |
|
|
|
|
|
16.19. |
|||
|
|
|||||||||
16.20. |
|
|
16.21. |
|
|
|
|
16.22. |
||
|
|
|
|
|
|
|||||
Вычислите объем тела, полученного вращением фигуры ограниченной линиями:
16.23. |
|
|
|
вокруг оси |
16.24. |
|
|
|
|
вокруг оси |
|
16.25. |
|
|
|
|
16.26. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16.27. |
|
|
|
|
16.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.29. |
|
|
|
|
16.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.31. |
|
|
|
|
16.32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Определите площадь поверхности, образованной вращением кривой:
16.33.


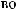


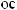
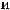
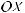
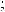
16.34.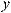

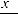
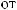


16.35.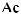

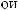
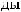
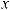

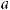
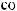

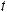
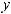

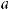
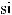
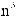
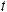
16.36.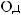
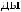
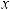

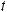

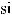
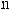
ОТВЕТЫ
16.1. 36; 16.2. 8 In 2; 16.3. 12; 16.4. |
|
; 16.5. 0,5; 16.6. |
|
; 16.7. 2; 16.8. |
|
; |
|
|
|
16.9. π / 2 – 1; 16.10. 2 – 1 / In 2; 16.11. 6π; 16.12. 9π / 2; 16.13. π / 4; 16.14. π / 4 + 2; 16.15. 5π 6−
6−
 3; 16.16. 4π
3; 16.16. 4π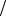 3 +2
3 +2
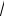 3; 16.17. 278 (10
3; 16.17. 278 (10
 10 −1); 16.18. π
10 −1); 16.18. π 
 2
2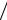 2; 16.19. 8; 16.20. 3 /2 16.21.
2; 16.19. 8; 16.20. 3 /2 16.21. 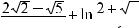
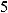
 16.22. 16; 16.23. 32π/3; 16.24. 18π; 16.25. 12π; 16.26.
16.22. 16; 16.23. 32π/3; 16.24. 18π; 16.25. 12π; 16.26. 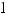
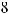
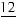

16.27. 2048π/35; 16.28. 64π/3; 16.29. 16π; 16.30. 10,6π; 16.31. 128π/3; 16.32. 5π2; 16.33. 16π; 16.34. 14π/3; 16.35. 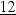

 16.36. 64π/3.
16.36. 64π/3.
37

17. Комплексные числа, действия над ними
Комплексным числом называется число вида: z = x + iy, где x, y R и i 2 = –1, x = Re z, y = Im z – соответственно действительная и мнимая части комплексного числа.
Данное число можно записать в тригонометрической форме z = r (cosφ + isinφ), где r и φ –
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
модуль и аргумент комплексного числа. Они находятся по формулам: r = |
|
z |
|
= x2 + y2 , |
|||||||||||||
|
|
||||||||||||||||
|
|
cosϕ = |
x |
|
sin ϕ = |
y |
|
tgϕ = |
y |
|
|
|
|
|
|
|
|
ϕ = |
π , |
, |
, |
, причем главное значение аргумента |
|||||||||||||
r |
r |
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
определяется следующим образом:
Существует также показательная форма записи комплексного числа:
z = reiϕ, где 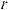

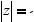
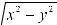
Действия над комплексными числами
Пусть z1 = x1 + iy1 и z2 = x2 + iy2 – комплексные числа, тогда: 1. 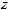



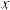


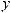

2.z1 + z2 = (x1 + x2) + i (y1 + y2).
3.z1 – z2 = (x1 – x2) + i (y1 – y2).
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z n = r n (cosnφ + isinnφ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
6. |
|
z1 |
= |
x1x2 + y1 y2 |
+i |
y1x2 − x1 y2 |
= |
r1 |
|
(cos(ϕ −ϕ |
|
)+isin(ϕ −ϕ |
|
)). |
|||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
||||||||||||||||||||||
|
|
z |
2 |
|
x2 |
+ y2 |
|
x2 |
+ y2 |
|
|
|
|
|
1 |
2 |
|
|
1 |
|
2 |
|
|||||||||
|
|
|
2 |
2 |
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи |
|
|
|
|
, k = 0.1, ..., n–1. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
17.1.Найдите 2z1 +3z2 ; z2 −4z1; z1 z2 , если z1 = 3 +4i, z2 |
= 2 −5i. |
|
|
|
|||||||||||||||||||||||||||
17.2. |
Вычислите |
|
3 −i |
|
|
2 |
|
|
|
|
33 |
|
((11++i)(3 +i) |
|
(1 |
−i)(3 −i) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
; (2 − 2i) |
|
; (1− |
|
3ii));; |
|
|
3 −i |
|
− |
|
|
. |
|
||||||||||||||||
|
4 +5i |
|
|
|
|
|
|
|
3 +i |
|
|||||||||||||||||||||
17.3.Представьтеследующиечиславтригонометрическойформе:z1 = 1 +i;z2 =3i; z3 = −2
 3 + 2i; z4
3 + 2i; z4
2i; z4 =1− |
|
|
; |
3i. |
|||||||||||
33ii; |
|||||||||||||||
17.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17.5.Решите уравнение а) |
z2 +6z +10 = 0; б) z3 +1 = 0; в) z4 −16i = 0 . |
||||||||||||||
ОТВЕТЫ
17.1. 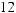




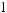


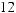
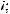


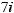
 17.2.
17.2.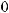
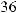

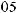
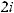

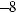
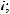

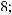
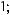 17.3.
17.3.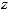


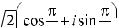


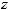

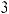

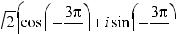
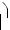
 .
.
38
Библиографический список
1.Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов /
Н.С. Пискунов. – В 2 т. Т. 1. – М.: Наука, 1975. – 456 с.
2.Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. – В 3 ч.
Ч. 1. – М.: Айрис-пресс, 2004. – 256 с.
3.Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевников. – 6-е изд. – В 2 ч. Ч.1. – М.: Издательство «Мир и Образование», 2005. – 304 с.
|
Содержание |
|
Введение................................................................................................................................. |
3 |
|
1. |
Функция, ее область определения и значений, график и свойства........................... |
4 |
2. |
Кривые второго порядка............................................................................................... |
6 |
3. |
Предел функции............................................................................................................. |
8 |
4. |
Замечательные пределы. Сравнение бесконечно малых и бесконечно больших |
|
|
функций.......................................................................................................................... |
10 |
5. |
Непрерывность функции. Точки разрыва................................................................... |
12 |
6. |
Производная функции. Правила и формулы дифференцирования.......................... |
14 |
7. |
Логарифмическое дифференцирование. Дифференциал функции. Производная |
|
|
параметрически заданных функций............................................................................ |
16 |
8. |
Производная неявных и параметрически заданных функций. Производные |
|
|
и дифференциалы высших порядков........................................................................... |
18 |
9. |
Применение производной к решению задач............................................................... |
20 |
10. |
Понятие и свойства неопределенного интеграла. Непосредственное интегри- |
|
|
рование........................................................................................................................... |
24 |
11. |
Методы интегрирования: метод подведения под знак дифференциала, метод |
|
|
замены переменной и метод интегрирования по частям........................................... |
26 |
12. |
Интегрирование рациональных функций................................................................... |
28 |
13. |
Интегрирование тригонометрических и иррациональных выражений.................... |
30 |
14. |
Определенный интеграл. Методы вычисления определенногоинтеграла............ |
32 |
15. |
Несобственные интегралы............................................................................................ |
34 |
16. |
Приложения определенного интеграла....................................................................... |
35 |
17. |
Комплексные числа, действия над ними..................................................................... |
38 |
Библиографический список............................................................................................... |
39 |
|
39
