
ВМ26
.pdf
9. Применение производной к решению задач
Функцияy = f (x) возрастает(убывает)намножествеX,еслидлялюбыхx1,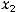
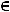
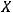 ,таких,
,таких,
что x1< x2 , выполняется неравенство f (x1) < f (x2) (f (x1) > f (x2)).
Если на каком-то промежутке функция y = f (x) возрастает (убывает) и дифференцируема на этом промежутке, то f ' (x) ≥ 0 (f ' (x) ≤ 0), причем равенство нулю не может быть на промежутке ненулевой длины.
Верно и обратное утверждение: если на каком-то промежутке f ' (x) ≥ 0 ( f ' (x) ≤ 0), причем равенство f ' (x) = 0 достигается лишь в конечном числе точек этого промежутка, то функция y = f (x) на этом промежутке возрастает (убывает). Отсюда следует, что если производная в точке x0 меняет знак с «+» на «-» (с «-» на «+»), то функция y = f (x) в этой точке меняет возрастание на убывание (убывание на возрастание). Тогда точку x0 называют точкой максимума (минимума), а значение функции y = f (x) в этой точке функция – максимумом
(минимумом).
Значение f (x0) функции f (x) в точке x0 называется наибольшим (наименьшим) значением этой функции, если для любого x из D( f ) выполняется неравенство f (x0)>f (x) (f (x0)<f (x)).
Дифференцируемая на (а; b) и непрерывная на [а; b] функция y = f (x) достигает своего наибольшего (наименьшего) значения на границе отрезка [а; b] или в одной из точек экстремума на интервале (а; b).
График дифференцируемой функции y = f (x) называется выпуклым вниз (или вогнутым)
на (а; b), если дуга кривой y = f (x) x (a;b) расположена выше любой касательной, проведенной к графику этой функции.
График дифференцируемой функции y = f (x) называется выпуклым вверх (или выпуклым)
на (а; b), если дуга кривой y = f (x) x (a;b) расположена ниже любой касательной, проведенной к графику этой функции. Точки М (x0 ; f (x0)) графика дифференцируемой функции y = f (x), в которой направление выпуклости меняется на противоположное,
называется точкой перегиба.
Если функция y = f (x) на (а; b) дважды дифференцируема и f ' (x) > 0 х (a,b) , то график этой функции на (а; b) вогнутый (выпуклый вниз), а если f ' (x) < 0 х (a,b), то график этой функции на (а; b) выпуклый. Если для функции y = f (x), вторая производная f '' (x) в некото-
рой точке x0 обращается в ноль или не существует и при переходе через нее меняет свой знак, |
||
то М (x0 ; f (x0)) является точкой перегиба. |
|
|
Применяя производные, можно раскрывать неопределенности вида |
и |
. Заметим, |
что если функции y = f (x) и y = φ (x) непрерывны и дифференцируемы в окрестности точки x0 и обращаются в ноль в этой точке f (x0) = φ (x0) = 0, причем φ' (x) ≠ 0 в окрестности точки
x или в этой окрестности |
lim f (x)= lim ϕ(x)= ∞, φ' (x) ≠ 0, то |
lim |
f (x) |
= lim |
f ′(x) |
=l . Эта |
||||
ϕ(x) |
|
ϕ (x) |
|
|||||||
0 |
x→x0 |
x→x0 |
x→x0 |
x→x0 |
|
|||||
|
|
′ |
|
|||||||
формула имеет место и в тех случаях, если а) функции y = f (x) и y = φ (x) не определены
в точке x0 , но |
lim f (x)= 0 и lim ϕ(x)=0 , б) если x → ∞, в) ее можно применять еще раз, если |
|
|
x→x0 |
x→x0 |
f ' (x0) = φ' (x0) = 0 и производные f ' (x) и φ' (x) удовлетворяют тем же условиям что и функция f (x) и φ (x). Это так называемое правило Лопиталя.
Асимптотой графика функции y = f (x) называется прямая линия, обладающая тем свойством, что расстояние от точки на графике до прямой стремится к нулю при неограниченном удалении точки по графику от начала координат. Различают асимптоты вертикальные (параллельные 0y) и наклонные. Частным случаем наклонной асимптоты является горизонтальная асимптота. Прямая x = x0 называется вертикальной асимптотой графика функции y = f (x), если хотя бы
20

один из односторонних пределов в точке x0 |
равен бесконечности, то есть lim f (x)= ±∞ |
|
x→x0 −0 |
или lim f (x)= ±∞ . Для того чтобы график функции y = f (x) имел наклонную асимптоту |
|||||||
x→x0 +0 |
|
f (x) |
|
|
|
||
y = kx + b,необходимоидостаточно,чтобысуществовали |
lim |
= k |
и |
lim (f (x)−kx)=b. |
|||
x |
|
||||||
|
k→±∞ |
|
|
k→±∞ |
|||
Общая схема исследования функции и построение ее графика
Исследование функции y = f (x) целесообразно вести в определенной последовательности:
1.Найти область определения функции.
2.Выяснить, является ли функция четной, нечетной или общего вида. Указать период функции, если она периодическая.
3.Найти (если это возможно) точки пересечения графика с осями координат.
4.Найти область непрерывности функции, точки разрыва и вертикальные асимптоты.
5.Найти наклонные асимптоты графика функции.
6.Найти интервалы монотонности и точки экстремума функции.
7.Найти интервалы выпуклости и точки перегиба графика функции.
Задачи
Найдите интервалы монотонности и экстремумы функций:
|
|
|
|
|
|
9.3. y = 3 |
|
. |
9.2. |
|
|
|
|
|
(x2 −6x +5)2 |
||
|
|
|
|
|
Найдите наибольшее и наименьшее значения функции на отрезке:
9.4. y = 2x3 +3x2 −12x; |
x [−1;2] |
9.5. y = x +33 |
|
; x [−1;1] |
||||||||||||
x |
||||||||||||||||
Найдите точки перегиба, |
|
|
|
|
|
и вогнутости графика функции: |
||||||||||
9.6. y = x3 −3x2 −9x +7; |
|
|
|
|
|
|
|
|
|
|
|
9.8. y = arctgx− x. |
||||
Найдите асимптоты графика функции: |
|
|
|
|
|
|
|
|
|
|
||||||
9.9. |
|
|
|
|
9.10. |
|
|
|
|
|
|
|
|
|
|
9.11. y = xe1x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проведите полное исследование функции и построить ее график:
9.12. y = x3 −3x2 ; |
9.13. |
y = x2 + |
2 |
; |
9.14. |
|
|
|
9.15. y = x ex . |
|
x |
||||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
9.16.Найти высоту конуса наибольшего объема, который можно вписать в шар радиусом R.
9.17.Через точку М (1; 4) провести прямую так, чтобы сумма величин положительных отрезков, отсекаемых ею на осях координат, была наименьшей. Записать уравнение этой прямой.
9.18.Три пункта А, В, и С расположены так, что угол АВС равен 60°. Из А в В движется автомобиль со скоростью 80 км/час, из В в С – поезд со скоростью 50 км/час. Через сколько времени расстояние между поездом и автомобилем будет наименьшим, если движение началось одновременно и АВ = 215 км?
9.19.Окно имеет форму прямоугольника, завершенного полукругом. Периметр равен р.
Каковы должны быть размеры окна, чтобы оно пропускало наибольшее количество света? Вычислите пределы с помощью правила Лопиталя:
9.20. |
|
|
|
|
|
|
|
9.21. |
|
|
|
9.22. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.23. |
|
|
|
|
9.24. |
|
|
9.25. |
|||||
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||
21

Формулы Тейлора и Маклорена
Если функция f (x) определена в некоторой окрестности точки x0 и имеет в ней производные до (n+1)-го порядка включительно, то для любого х из этой окрестности найдется точка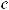
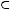


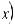
такая, что справедлива формула:
f (x)= f (x |
|
)+ |
f ′(x0 ) |
(x − x |
|
)+ |
f ′′(x0 ) |
(x − x |
|
)2 |
+...+ |
f n (x0 ) |
(x − x |
|
)n + |
f (n−1)(c) |
(x − x |
|
)n+1 |
|
0 |
|
1! |
|
0 |
|
2! |
|
0 |
|
|
n! |
0 |
|
(n+1)! |
0 |
|
||
где c = x0 +θ(x − x0 ),θ (0;1).
Эта формула называется формулой Тейлора для функции f (x). Эту формулу можно записать в виде:
|
|
|
|
|
|
f (x)= Pn(x)+ Rn(x), |
|||
где P (x)= |
f (x |
)+ |
f ′(x0 ) |
(x − x |
)+...+ |
f (n)(x0 ) |
(x − x |
0 |
)n – многочлен Тейлора; |
|
|
||||||||
n |
|
0 |
1! |
|
0 |
n! |
|
||
|
|
|
|
|
|
|
|||
Rn(x)= f (n+1)(c)(x − x0 )n+1 – остаточный член формулы Тейлора в форме Лагранжа.
Rn(x) – есть погрешность приближенного равенства f (x)≈ Pn(x).
Таким образом, формула Тейлора дает возможность заменить функцию y = f (x) многочленом)≈ Pn(x)с соответствующей степенью точности.
При x0 = 0 получаем частный случай формулы Тейлора – формулу Маклорена:
|
f (0) |
|
f (0) 2 |
f |
(n) |
(0) |
n |
f |
(n+1) |
(c) |
n+1 |
||||
f (x)= f (0)+ |
′ |
x + |
′′ |
x +...+ |
|
|
|
|
x + |
|
|
|
x |
, |
|
1! |
|
2! |
|
n! |
|
(n+1)! |
|||||||||
где c =θ x,θ (0;1).
Рассмотреннаяранееформуладляприближенныхвычислений f (x)≈ f (x0 )+ f ′(x0 )(x − x0 ) является частным случаем более точной формулы:
f (x)≈ f (x |
)+ |
f ′(x0 ) |
(x − x |
0 |
)+ |
f ′′(x0 ) |
(x − x |
0 |
)2 |
+...+ |
f n (x0 ) |
(x − x |
0 |
)n |
|
0 |
1! |
|
|
2! |
|
|
|
n! |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Задачи
9.26.Разложите многочлен P(x)= x3 +4x2 −6x −8 по степеням x + 1.
9.27.Разложите по формуле Тейлора функцию f (x)= 1x в точке x + 1.
9.28.С точностью до 0,0001 вычислите sin10, использую формулу Маклорена.
9.29.Используя формулу Маклорена, докажите неравенство ln(1+ x) < х.
9.30.Используя формулу Маклорена, вычислите пределы:
|
|
|
|
|
е |
−х2 |
2 |
−cos x |
|
|
х−ln(1+ х) |
|
|
|
|
||||||
|
а) |
|
lim |
|
|
; |
б) |
lim |
|
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
х |
4 |
x→0 |
|
|
|
|
|
|
||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|||
9.16. |
|
4R |
; |
9.17. y = -2x + 6; 9.18. |
105 |
мин.; |
9.19. |
p |
; |
2 p |
; |
9.20. -2; 9.21. 0; 9.22. 1; |
|||||||||
3 |
π +4 |
π +4 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9.23. 1; 9.24. ∞; 9.25. -0,5; 9.28. 0,0175; 9.30. а) 112 ; б) 0,5.
22
Подготовка к контрольной работе по теме «Производная функции»
Приведены два варианта, идентичные вариантам контрольной работы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 101 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Вариант 100: 1. − |
sin(ln x) |
; |
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 3. |
|
|
9e3x (1− x) |
; 4. |
|
|
|
|
|
1 |
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 −3x)2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(t −2) 1−t |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
4 x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
2x2 y2 − y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−dx |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
5. |
|
|
|
sin |
|
|
|
|
|
|
|
|
xctg |
|
|
|
+ |
4 ln sin |
|
|
; |
6. |
|
|
|
|
|
|
|
|
|
|
; |
7. 30( |
|
|
|
|
5x −1); |
8. |
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
x − x3 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
cos 2x |
|
|
|||||||||||||||||||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
; 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2arctgx |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Вариант |
101: 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 3. |
|
|
|
|
|
|
|
|
; 4. |
; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ x2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
6x sin2 x − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2sin 3x |
|
|
|
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
6. |
|
(2x |
|
−1) |
|
|
|
3cos 3x ln(2x −1) |
+ |
|
|
|
|
|
|
|
; |
7. |
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||
|
|
sin2 |
x(ctgx+2x3 )ln10 |
|
|
|
|
2x −1 |
|
2xe−xy − y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
; 9. 480(3 −4x)4 ; |
10. 4сtg4t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
23

10. Понятие и свойства неопределенного интеграла. Непосредственное интегрирование
Функция F (x) называется первообразной для функции f (x) на некотором промежутке, если для всех значений x из этого промежутка выполняется равенство F ' (x) = f (x) или, что тоже самое, dF (x) = f (x)dx.
Если F (x) – первообразная функции y = f (x), то выражение F (x) + C, где C – произвольная постоянная, называется неопределенным интегралом от функции f (x) и отображается
символом 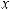
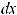 .Функция f (x) называется подынтегральной функцией, переменная x – переменной интегрирования.
.Функция f (x) называется подынтегральной функцией, переменная x – переменной интегрирования.
Основные свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции, то есть:
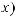
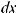

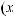
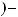
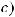

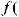
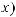 .
.
а. Дифференциал от неопределенного интеграла равен подынтегральному выражению: d(∫ f (x)dx)= d(F(x)+c)= d(F(x))= f (x)dx.
2.Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс постоянная ∫dF(x)= F(x)+c .
3.Постоянный множитель можно вынести из-под знака интеграла, т.е. 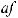
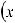
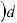
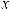

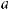
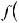
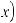
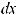 .
.
4.Неопределенный интеграл от алгебраической суммы равен алгебраической сумме интегралов от каждой функции в отдельности 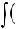
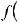
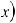
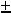
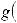
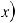
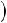
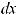
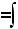
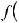
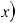
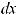
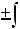
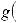
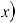
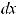 .
.
5.При вычислении неопределенных интегралов бывает полезно использовать следующие правила: если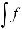
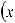
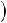
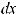
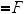
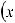
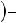
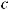 , то:
, то:
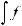
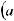
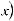
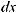

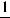
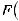

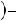
 ;
;
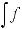
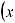
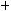
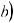
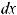

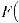
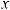
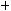
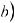
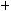
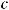 ;
;
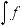
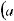
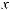
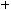
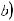
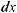

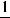
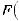
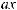
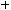
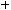
 .
.
6.Пусть дан интеграл, в котором подынтегральное выражение может быть записано в виде f (u)du, где u = φ (x) – любая дифференцируемая функция и, следовательно, d (u) = φ' (x) dx. Иными словами f (u)du = f (φ(x)) φ' (x) dx , тогда:
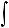
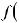
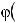
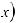
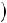

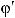

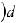


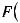
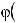
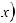
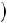
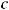 или
или 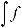

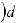
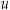

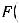
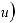
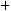
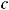 .
.
Таким образом, формула для неопределенного интеграла остается справедливой, независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Таблица основных интегралов
24

|
|
|
|
|
Задачи |
|
|
|
|
|
|
Внесите функции под знак дифференциала: |
|
|
|
|
|
|
|||||
10.1. |
10.2. |
10.3. |
|
|
|
|
10.4. |
||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10.5. |
10.6. |
10.7. |
10.8. |
||||||||
10.9. |
|
|
|
10.10. |
10.11. |
|
|
10.12. |
|||
|
|
|
|
||||||||
Найдите интегралы:
10.13. 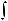
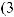
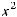

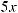
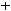
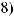
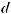 10.16.
10.16. 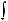
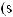

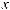

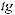
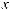

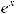 10.19.
10.19. 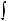
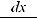
 10.22.
10.22. 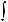
 10.25.
10.25. 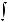
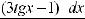

10.28. 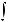
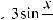

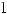

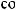
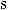 10.31.
10.31. 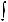

10.34. 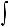
10.37. 
10.14. |
10.15. |
10.17. |
10.18. |
10.20. |
10.21. |
10.23. |
10.24. |
10.26. |
10.27. |
10.29. |
10.30. |
10.32. |
10.33. |
10.35. |
10.36. |
10.38. |
10.39. |
|
ОТВЕТЫ |
10.1. |
1 d(x +5)2 |
; |
10.2. |
|
|
2d |
|
|
|
|
|
|
10.3. |
1 d ln |
|
|
1 d ln |
|
3 |
−2x |
|
; |
10.5. −d cos x; |
||||||||||
x +2; |
4x −1; |
10.4. − |
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
(4x +3)34 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 d sin 3x; |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
10.6. |
|
10.20. |
|
|
|
+C; |
10.21. |
|
+C; |
10.22. |
|
x2 −4 +C; |
|||||||||||||||||||||
|
35−25x |
|
|
||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10.26. |
− |
ln |
|
4ctg3x −1 |
|
|
+C; |
10. |
|
|
|
|
|
|
10.34. |
|
|
− |
|
|
|
1 |
|
+C; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
ln 7(7x−1 +5)7 |
||||||||||||||||||
10.36. |
− 1 arcctg2 |
x |
+C; 10.38. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
6 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25

11. Методы интегрирования: метод подведения под знак дифференциала, метод замены переменной и метод интегрирования по частям
Метод подведения под знак дифференциала
Пусть требуется вычислить интеграл вида ∫ f (ϕ(x)) ϕ′(x)dx. По определению дифферен-
циала ∫ϕ′(x)dx = d(ϕ(x)), тогда ∫ f (ϕ(x)) ϕ′(x)dx = ∫ f (ϕ(x)) d(ϕ(x)) = ∫ f (u)du.
При интегрировании методом «подведения под знак дифференциала» используют свойство дифференциала:
du = d(u +a);du = 1a d(au);udu = 12 d(uu22););cos udu = d(sinu); u1 du = d(lnu)и т д.
С другой стороны, для нахождения неопределенного интеграла и для подведения под знак дифференциала используют табличные интегралы:
∫x2dx = 13 x3 +c x2dx = 13 d(x3 ), 
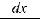
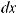

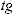
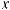
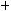
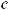



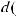

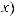 и т.д.
и т.д.
Метод замены переменной
Пусть требуется найти интеграл ∫ f (x)dx . Сделаем замену переменной в подынтегральном
выражении, положив x = φ(t), где φ(t) – непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx = φ'(t)dt и на основании свойства инвариантности формулы интегрирования получаем формулу интегрирования подстановкой:
∫ f (x)dx = ∫ f (ϕ(t)) ϕ′(t)dt.
Функцию x = φ(t) следует выбирать так, чтобы можно было вычислить неопределенный интеграл непосредственно.
Метод интегрирования по частям
Пусть u и v – две дифференцируемые функции от x. Тогда:
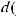
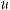

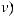

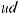
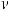
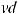



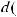
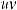
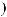


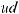
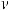
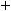

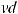
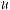

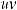


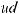
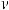

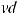
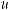 ,
,
или ∫udv =uv −∫vdu – это формула интегрирования по частям.
Иногда для получения окончательного результата нужно метод интегрирования по частям применять последовательно несколько раз.
Часто встречающиеся интегралы, которые вычисляются данным методом:
1. |
Интегралы вида |
∫P(x)ekxdx; ∫P(x)sin kxdx; ∫P(x)cos kxdx, где P(x) |
– |
многочлен, |
|
|
|
kx |
|
|
|
|
|
e |
|
|
|
|
k – некоторое число. Здесь u = P(x) и dv = sin kx dx . |
|
|
||
|
|
|
|
|
|
|
|
cos kx |
|
|
|
2. |
Интегралы вида |
∫P(x)ln xdx; ∫P(x)arcsin xdx; ∫P(x)arctgxdx, где P(x) |
– |
многочлен. |
|
|
|
ln x |
|
|
|
В этом случае dv = P(x)dx и u = arcsin x .
arctg x
26

3.Интегралы вида ∫eax sin bxdx; ∫eax cosbxdx, где a и b – числа. Эти интегралы вычисляются двукратным интегрированием по частям.
Найдите интегралы: |
|
|
|
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
11.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
11.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
11.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
11.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.29. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11.31. |
; |
|
|
|
|
11.32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.33. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
11.34. |
|
|
|
|
11.35. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.36. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
11.37. |
|
|
|
|
|
|
|
|
|
|
|
|
|
11.38. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex +1 |
−1 |
|
|||||
11.19. |
|
2arctg 3x −1 +C; |
11.20.−2 x −8ln |
4 |
− x |
+C; |
11.24. |
|
|
|
|
|
|
ln |
|
|
+C; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ex +1 |
+1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3x (9x2 − |
|
|
|
|
|
x2 +1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
11.28. |
(4x +6)sin |
x |
|
+8cos |
x |
|
+C; 11.30. |
|
6x −7)+C; |
11.32. |
|
arcctgx+ |
x |
+С. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||
27

12. Интегрирование рациональных функций
Всякую рациональную функцию можно представить в виде рациональной дроби, т.е. в виде отношения двух многочленов:
Pn (x) = a0 + a1 x +...+ anxn . Qm (x) b0 +b1 x +...+bm xm
Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае – неправильная. Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:
|
P(x) |
= S(x)+ |
R(x) |
|
, где S(x) – многочлен, а |
|
R(x) |
– правильная дробь. |
|||||||||||
|
Q(x) |
|
|
Q(x) |
|
|
|
|
|
|
Q(x) |
|
|
|
|||||
Правильные рациональные дроби вида: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
I. |
A |
; |
II. |
|
|
|
A |
|
; III. |
Ax + B |
; |
IV. |
|
Ax + B |
|
, |
|
|
|
x − a |
|
(x − a)k |
x2 + px +q |
(x2 + px +q)k |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где k ≥ 2 – целое |
число; |
p2 |
−4q |
< 0 , называются |
простейшими. |
Каждая правильная |
|||||||||||||
|
|
|
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей.
Так как всякий многочлен с вещественными коэффициентами степени выше второй можно разложить единственным образом на линейные и квадратные множители с вещественными коэффициентами, то пусть для определенности:
Q(x) = (x −a1 )k1 (x −a2 )k2 ...(x −as )ks (x2 + p1x +q1 )r1 ...(x2 + pm x +qm )rm .
Разложение знаменателя Q(x) рациональной дроби на множители тесно связаны с разложением дроби на простейшие, при этом необходимо знать:
1. Каждомунеповторяющемусямножителювида(x – a)соответствуетвразложенииодна
A
простая дробь x −a .
2.Каждому множителю (x – a)k отвечает сумма k простых дробей вида
xA−1 a + (x −A2a)2 + (x −A3a)3 +...+ (x −Aka)k .
3.Неповторяющемуся множителю x2 + px + q отвечает в разложении одна дробь вида
Mx + N |
. |
x2 + px +q |
|
4. Каждому множителю (x2 + px + q)r отвечает r простых дробей вида
.
Таким образом, зная разложение Q(x), известны знаменатели всех тех простых дробей, на которыеразлагаетсяданнаядробь QP((xx)) .ОстаетсятолькоопределитькоэффициентыA,M,N.
Наиболее простыми методами определения коэффициентов в разложении правильной дроби на простейшие является метод неопределенных коэффициентов и метод частных значений.
28
Задачи
Вычислите интегралы:
12.1. 
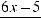
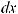
 12.3.
12.3. 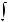


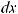

12.5. 
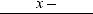
 12.7.
12.7. 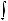

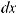
 12.9.
12.9. 

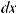
 12.11.
12.11. 
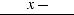
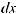
 12.13.
12.13. 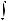

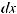
 12.15.
12.15. 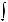
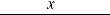
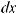
 12.17.
12.17. 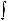
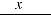
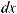
 12.19.
12.19. 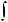

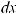
 12.21.
12.21. 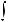

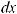
 12.23.
12.23. 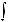

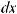

12.2. 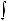


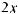
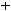
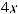
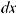
 12.4.
12.4. 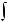


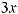

 12.6.
12.6. 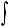
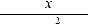
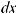
 12.8.
12.8. 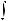

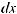

12.10. 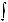
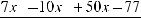
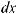
 12.12.
12.12. 

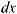
 12.14.
12.14. 
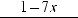
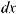
 12.16.
12.16. 
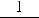
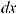
 12.18.
12.18. 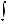

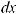
 12.20.
12.20. 

 12.22.
12.22. 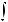
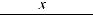
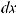
 12.24.
12.24. 

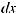

ОТВЕТЫ
12.1. |
−1,2х+0,76ln |
|
1−5х |
|
+С; |
12.2. |
|
1 х3 |
− 3 |
|
х2 |
+7х−7ln |
|
|
х+1 |
|
+С; 12.5. ln |
(х−1) |
|
|
х−2 |
|
|
+С; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
х3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
3 ln |
|
|
|
|
|
|
|
3 ln |
|
|
|
|
− 1 arctgx+C; 12.9. 2 ln |
|
|
|
|
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
12.6. ln |
|
|
− |
|
|
|
|
+C; 12.7. |
|
x −1 |
|
− |
|
x2 |
+1 |
|
|
|
+ |
|
|
+C; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x +1 |
|
x +1 |
|
|
|
|
|
x +2 |
x +2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
12.12. |
4 ln |
|
x −5 |
|
+C; 12.13. 2 arctg |
x +1 |
+C; 12.14. −3,5ln |
|
x2 +7x +13 |
|
−17 |
|
|
arctg |
|
2x +7 |
|
|
+C; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x +2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
7 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
12.15. ln |
|
x +1 |
|
+ |
|
|
|
+C; 12.17. − |
|
|
|
− |
|
|
+C; 12.19. x2 +6x +13 +2ln |
x +3 |
+ |
|
x2 +6x +13 |
+C. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x +2 |
|
x −2 |
|
2(x −2)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
29
