Teoria_uprugosti_Ch2_Ledovskoy_12

Теория упругости. Часть II

УДК539.3/8(07)

Рецензенты:

д-р техн. наук, профессор В. Б. Шпильман (СПбГПУ); канд. техн. наук, доцент Н. Б. Левченко (СПбГАСУ)

Ледовской, И. В.

Теория упругости: учеб.-метод. пособие. В 2 ч. Ч. II / И. В. Ледовской, В. В. Рощин, О. Б. Халецкая, Г. С. Шульман; СПбГАСУ. –

СПб., 2012. – 83 с.

ISBN 978-5-9227-0349-9

Пособиесостоитиздвухчастей:впервой–текстызадачкурсовойработы, во второй – методические указания по решению этих задач.

Предназначено для выполнения курсовой работы студентами, обучающимися по специальностям 270205 – автомобильные дороги и аэродромы и 270201 – мосты и тоннели, а также может быть использовано студентами других строительных специальностей при изучении основ теории упругости.

Табл. 4. Ил. 41. Библиогр.: 6 назв.

РекомендованоРедакционно-издательскимсоветомСПбГАСУ в качестве учебного пособия.

Предисловие

Курсоваяработапотеорииупругостипредполагаетрешениеряда задач, и студенты должны представить эту работу до экзамена (зачета) в установленные сроки. Методические указания должны облегчить выполнение этих задач и повысить эффективность изучения теории упругости.

Вовторойчастиучебно-методическогопособияприведеныпри- меры решения следующих задач:

•исследование напряженно-деформированного состояния

вточке;

•определение статических и кинематических граничных условий на контуре пластинки;

•определение внешних нагрузок, приложенных к телу, в простейших задачах теории упругости обратным методом;

•исследование изгиба прямоугольной полосы;

•исследование поперечного изгиба тонких плит. Теоретический материал, необходимыйдля решения этих задач,

изложен в ряде учебников, список которых приведен в конце второй частиучебногопособия.Таккаквтеорииупругостииспользуютсяразличные обозначения даже в одной и той же системе координат, в методических указаниях приведенасистема обозначений,котораярекомендуется студентам при выполнении указанной работы (см. ч. 1).

Перед выполнением каждой задачи рекомендуется ответить на вопросы по самоконтролю, приведенные в первой части.

Теория упругости. Часть II

Задача 1. ИССЛЕДОВАНИЕ НАПРЯЖЕННОДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА

Цель решения задачи – усвоение основ теории напряжений и деформаций. При этом предполагается, что напряженно-деформи- рованное состояние тела было определено ранее расчетами или экспериментально.

1.1. Напряженное состояние в точке тела

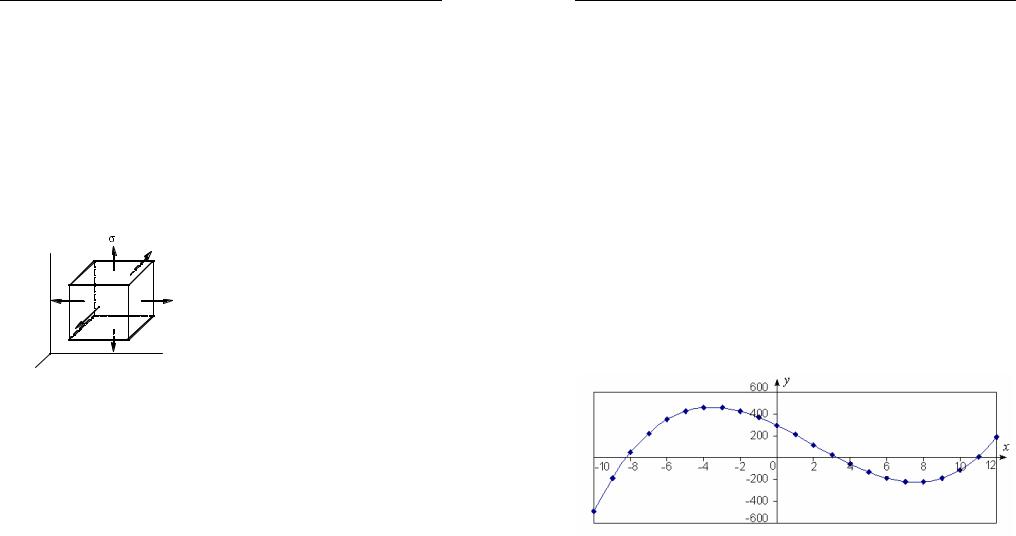
Мысленно вырежем в окрестности произвольной точки М нагруженного телаэлементарный (бесконечно малый) параллелепипед, грани которого перпендикулярны координатным осям x, y, z (рис. 1).

Условиезадачи.Компонентынапряжений,действующиепограням параллелепипеда, равны следующим величинам:

ке полностью определено, если известны шесть компонентов тензо-

ранапряжений σx ,σy , σz , τxy , τyz , τzx (см. рис. 1), т. е., зная эти шесть компонентов напряжений в точке, можно вычислить напряжения на

любой площадке, проходящей через эту точку.

4

Задача 1. Исследование напряженно-деформированного состояния в точке тела

1.1.1. Полное, нормальное и касательные напряжения на наклонной площадке

Найдем напряжения на некоторойнаклонной к осям x, y, z площадке, проходящей через заданную точку. Положение площадки относительно осей координат определяется направляющими косинусами l, m, n внешней нормали ν к этой площадке. Вначале вычисляем значения проекций на оси координат x, y, z полного напряжения pν по формулам

Зная проекции pνx , pνy , pνz полного напряжения, действующегопонаклоннойплощадке,можноопределить нормальное σν и касательное τν напряжения по формулам

σν = pνx l + pνy m + pνz n =

Теория упругости. Часть II

Полезно проверить правильность величин направляющих косинусов подстановкой их в выражение

которое должно превращаться в тождество.

Подставляя значения напряжений и направляющих косинусов в формулы (1.2), получим:

pνx = 40 0 − 40 0,866−50 0,5 = −59,6 МПа;

pνz = −40 0 +0 0,866−60 0,5= −30,0 МПа.

Составляющие полного напряжения, имеющие знак «минус», противоположны направлениям осей x и z . Положительная состав-

ляющая pνy направлена вдоль положительной оси y (см. рис. 2).

Значения pν , σν и τν , вычисленные по формулам

(1.3)–(1.5) с учетом заданных напряжений (1.1) и направляющих косинусов, имеют следующие значения:

pν = 96,2 МПа, σν = 44,8МПa;

τν =85,0 МПа.

Напряжение σν имеет

знак «плюс». Следовательно, Рис. 3 оно будет направлено от сече-

ния (рис. 3).

1.1.2. Вычисление проекции касательного напряжения на заданное направление

Направление касательного напряжения τν в плоскости сечения

свнешнейнормалью ν относительнолюбыхдвухортогональныхосей

ξи χ, лежащих в той же плоскости, определяется следующим образом..

Задача 1. Исследование напряженно-деформированного состояния в точке тела

мер, τνξ – проекцию полного напряжения pν на ось ξ. Обозначим

Здесь l, m, n – направляющие косинусы внешней нормали ν

к площадке, по которой действует касательное напряжение τν . Рассмотрим вновь трехгранную призму, показанную на рис. 3.

Найдем проекцию касательного напряжения τx , действующую по

площадкеВСКнаось ξ, т.е. касательноенапряжение τx ξ (см. рис.3). Внешняя нормаль к площадке ВСК совпадает с положительной

Вычислим касательное напряжение τxξ по формуле (1.9) с уче-

том (1.1), (1.10) и (1.11):

τx ξ = 40 1 0 +80 0 0,5−60 0 (−0,866)−(−40)[1 0,5+0 0] +

+0[0 (−0,866)+0 0] +50[0 0 +(−0,866) 1] = −63,3 МПа.

ле σ1 ≥ pν ≥ σ3 . Величины главных напряжений являются корнями кубического уравнения

I3 = σxσyσz + 2τxyτyzτzx −τ2xyσz −τ2yzσx −τ2zxσy .

I1, I2 , I3 – инварианты напряженного состояния, которые не меняются при повороте координатных осей.

Задача 1. Исследование напряженно-деформированного состояния в точке тела

Используя заданные напряжения (1.1), вычислим инвариан-

ты (1.13):

Чтобыуменьшить величиныкоэффициентов вуравнении(1.15),

воспользуемсяподстановкой σ =10x .Послепреобразованийполучим уравнение

Для отыскания корнейкубического уравнения имеются готовые формулы (см. справочники по математике), но ими пользоваться неудобно. В наше время можно пользоваться какой-либо вычислительной программой, например Mathcad. В этой программе очень просто построить график функции:

f (x) = x3 −6x2 −81x − 296.

Точки пересечения графика этой функции с осью абсцисс дадут корни полинома, т. е. значения, как это показано на рис. 6.

Рис. 6

Если устудента нет компьютераилион неумеетпользоваться комплексом Mathcad, то можно решить уравнение (1.15) «вручную», т. е. сначала путем подбора надо найти одно значение, обращающее в ноль полином в правой части (1.16). Допустим, этоx = 3,29. Затем де-

ление полинома (1.16) на (y −3,29) приводит к квадратномууравнению

Теория упругости. Часть II

Корнями этого уравнения будут два числа: –8,22 и 10,9. Следовательно, корнями уравнения (1.16) являются числа

Выполним проверку найденных значений главных напряжений, вычисливинварианты напряженного состоянияи сравнивих сисходными значениями (1.14):

I1 = σ1 +σ2 +σ3 = 60;

I2 = σ1σ2 +σ2σ3 +σ3σ1 ≈8090;

I3 = σ1σ2σ3 ≈ 296 000.

Разница междуинвариантамиприповороте осейкоординатвозникает за счет приближенного вычисления напряжений (1.18), и в нашем случае она меньше 1 %.

Если площадка, наклонная к осям x, y, z , является главной, то полное напряжение, действующее по этой площадке, будет перпен-

дикулярно к ней, т. е. pν = σν и его составляющие по осям координат

где l, m, n – направляющие косинусы нормалиν к главной площадке. Направляющие косинусы нормали ν к главной площадки найдем следующим образом. Подставим в уравнения (1.5) вместо pνx ,

pνy , pνz их выражения в виде (1.19) и получим систему уравнений

τzx l + τzy m + (σz −σν) n = 0.

Тривиальное решение системы уравнений (1.20) в виде l = m = n = 0 не может быть искомым решением, так как не будет выполняться соотношение (1.6)

Задача 1. Исследование напряженно-деформированного состояния в точке тела

l 2 + m2 + n2 =1.

Найдем искомые значения l, m, n , решая систему, состоящую из уравнения (1.6) и любых двух уравнений (1.20) (например, первых двух) при условии, что σν = σ1 =109МПа, а компоненты напряжения имеют значения в виде (1.1):

−40l +(80−109,3) m = 0.

Используя два последних уравнения (1.21), выразим l и n через m иподставим ихв первое уравнение (1.21). Такимобразом, получим квадратное уравнение относительно m, из которого определяем два значения m. После определения l и n из двух последних уравнений (1.20) получим окончательное решение системы уравнений (1.21) в виде

Возникновение двух наборов направляющих косинусов в качестве решения уравнений (1.21) связано с тем, что при повороте на 180° нормали к любой главной площадке изменяются только знаки направляющих косинусов этойнормали(рис.7).Точ-

ность вычисления l, m, n – направляющих косинусов нормали к первой главной площадке – проверяется путем подстановки в урав-

нение (1.6).

Таким образом, два набора направляющих косинусов соответствуют противоположным граням

элементарного параллелепипеда. Рис. 7

Теория упругости. Часть II

1.2. Деформированное состояние в точке тела

При нагружении в теле возникнут не только напряжения, но и деформации – изменения взаимногорасположения точектела. Рас-

смотрим деформации элементарного параллелепипеда со сторонами dx, dy, dz в окрестности точки тела М (рис. 8), по граням которого

действуют заданные компоненты тензора напряжений (1.1).

Связь между деформациями и напряжениями определяется линейными соотношениями обобщенного закона Гука:

где E – модуль упругости материала; µ – коэффициент Пуассона,

модуль сдвига G = 2(1E+µ).

По формулам(1.22) компоненты деформации в точке при задан-

ныхкомпонентахнапряжений(1.1)и E = 2 105 МПa, µ = 0,25 имеют следующие значения:

Согласно результатам вычислений отрезки MK и MD, направленные соответственно вдоль осей x и y на рис. 8, удлинятся, а отрезок МА укоротится; прямой угол между ребрами параллелепипеда вплоскости xy увеличится, вплоскости xz уменьшится, а в плоскости yz останется без изменений.

Рис. 8

Задача 1. Исследование напряженно-деформированного состояния в точке тела

Если известны три компоненты линейнойдеформации εx , εy , εz итрикомпо-

ненты угловой деформации γxy , γyz , γzx

в данной точке, то можно определить линейную деформацию в любом направлении и искажение угла между любыми взаимно перпендикулярными бесконечно малыми отрезками, проведенными из этой

точки. Рис. 9 Например,пустьизнекоторойточкиM

(рис. 9) нагруженного тела проведены три луча ν1,ν2 ,ν3 , имеющие соответствующие направляющие косинусы:

ν1(l1, m1, n1), ν2 (l2 , m2 , n2 ), ν3 (l3 , m3 , n3 ).

Ни один из этих лучей не параллелен осям x, y, z и, кроме того, лучи ν2 иν3 взаимноперпендикулярны,т.е.имеетместосоотношение

l2 l3 + m2 m3 + n1 n2 = 0.

Линейная деформация εν1 в направлении луча ν1 вычисляется по формуле

1.2.1. Определение линейной, угловой и объемной деформаций

Компоненты деформаций в точке тела M имеют, например, значения (1.23) и (1.24). Требуется вычислить линейную деформацию в

направлении ν1 (см. рис. 9), заданном направляющими косинусами относительно осей x, y, z (см. табл. 1.2 пособия, ч. 1):

Теория упругости. Часть II

Подставляявформулу(1.25)значениякомпонентовдеформации (1.23) и направляющих косинусов (1.27), получим

εν =1,75 10−4 0,82 + 4,25 10−4 0,52 − 4,5 10−4(−0,332)2 − −5 10−4 0,8 0,5+6,25 10−4 0,5(−0,332) = −1,35 10−4.

Знак «минус»означает, что в направлении ν1 произойдет укоро-

чение бесконечно малого отрезка, проведенного из точки М.

ДляопределенияугласдвигамеждуотрезкамиBAи BCна рис. 2

Подставляязначениякомпонентовдеформацииинаправляющих косинусов в (1.26), получим

γηξ = 2[1,75 10−4 0(−1)+ 4,25 10−4 0,5 0 −4,5 10−4(−0,866)0] −

−5 10−4[0 0 +(−1)0,5] +6,25 10−4[(−0,866)(−1)+ 0 0] = 7,91 10−4.

По закону Гука (1.22)

τηξ = Gγηξ = 0,8 10+5 7,9125 10−4 = 63,3 MПа.

напряжение τxξ = −63,3 МПа (см.рис.3),прикоторомуголмеждуося-

ми х и ξ увеличился. Так как ось η имеет направление, противоположное направлению оси х, то и

τηξ = −τxξ.

Задача 1. Исследование напряженно-деформированного состояния в точке тела

не зависит от ориентации осей x, y, z . Если подставить в (1.28) вместо εx , εy , εz их значения в виде (1.23), то получим εV =1,5 10−4 . Так

как эта деформация оказалась положительной, то в окрестности рассматриваемой точки произойдет увеличение объема.

Теория упругости. Часть II

Задача 2. ПОСТАНОВКА КИНЕМАТИЧЕСКИХ И СТАТИЧЕСКИХ ГРАНИЧНЫХ УСЛОВИЙ

Задачей теории упругости является определение напряжений, деформаций и перемещений в любой точке тела, возникающих при заданных объемных и поверхностных нагрузках, а также кинематических граничных условиях на его поверхности.

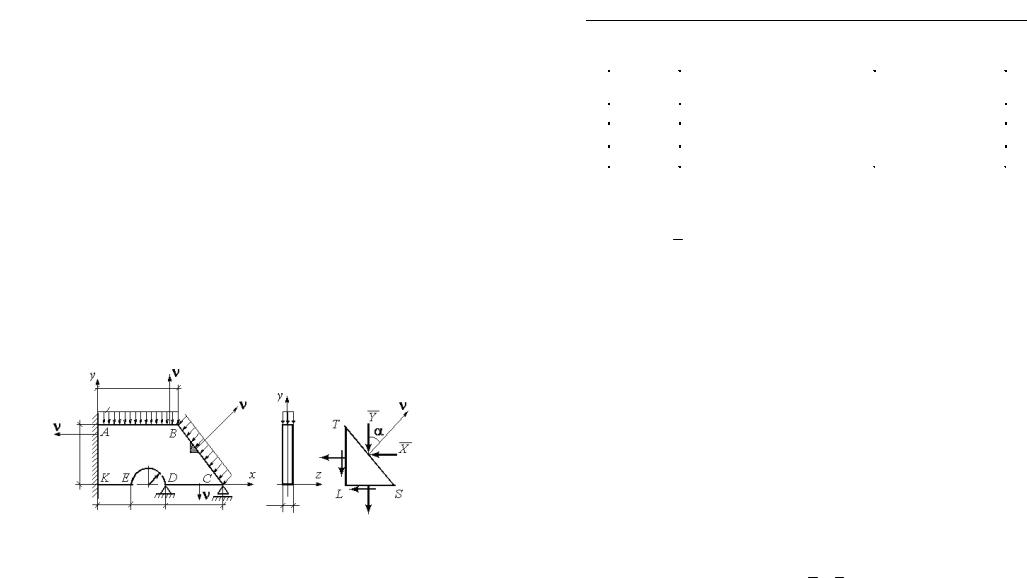
Рассмотрим вопрос о том, как задаются граничные условия на поверхности тела.

На тонкую пластинку, показанную на рис. 11, наложены связи, препятствующие перемещению пластинки как жесткого тела в плоскости xy . Любые перемещения точек пластинки происходят лишь за счет ее деформации. Эти перемещения разложим на составляющие u, v, w, параллельные соответствующим осям координат x, y, z . Ограничения, которыесвязинакладываютнаперемещенияточекконту-

ра пластинки, называют кинематическими граничными условиями.

Рис. 11

На участке AK контура пластинки (рис. 11, а) имеется жесткая связьпластинкиснеподвижнымиабсолютнотвердымтелом,длявсех точекконтактаобоихтелсоблюдаютсяусловия u = v = 0 .Контурпластинки в точках C и D имеет дискретные связи с тем же абсолютно твердымтелом.ПеремещенияточкиD контурапластинкиравнынулю, т. е. u = v = 0 . Из двух перемещений точки C в плоскости пластинки лишь одно, параллельное оси y , равно нулю, а другое, параллельное осиx,врезультатедеформацийпластинкиможетиметьместо(табл.2.1).

Задача 2. Постановка кинематических и статических граничных условий

Кпластинке приложены поверхностные нагрузки, параллельные

ееплоскости ираспределенныеравномерно по ее толщинеt (рис. 11,б). Проекция интенсивности поверхностных нагрузок вдоль оси z равна

нулю, т. е. Z = 0 ; кроме того, равны нулю и объемные силы X =Y = Z = 0 . В связи с этим напряженное состояние в любой точке

определяется только тремя компонентами напряжения: σx ,σy , τxy , лежащимиводнойплоскости.Этинапряженияможносчитатьпостоянными по толщине (составляющие напряжения σz , τzx , τzy равны

нулю в точках, прилегающих к боковым поверхностям пластинки, и без существенной ошибки можно предположить, что они обращаются в нуль и по толщине пластинки). Таким образом, в пластинке имеет место плоское напряженное состояние.

В дальнейшем обсуждении толщина пластинки не имеет значения, и этот размер полагается равным единице. Компоненты напря-

жения σx ,σy , τxy меняются непрерывно от точки к точке по всей

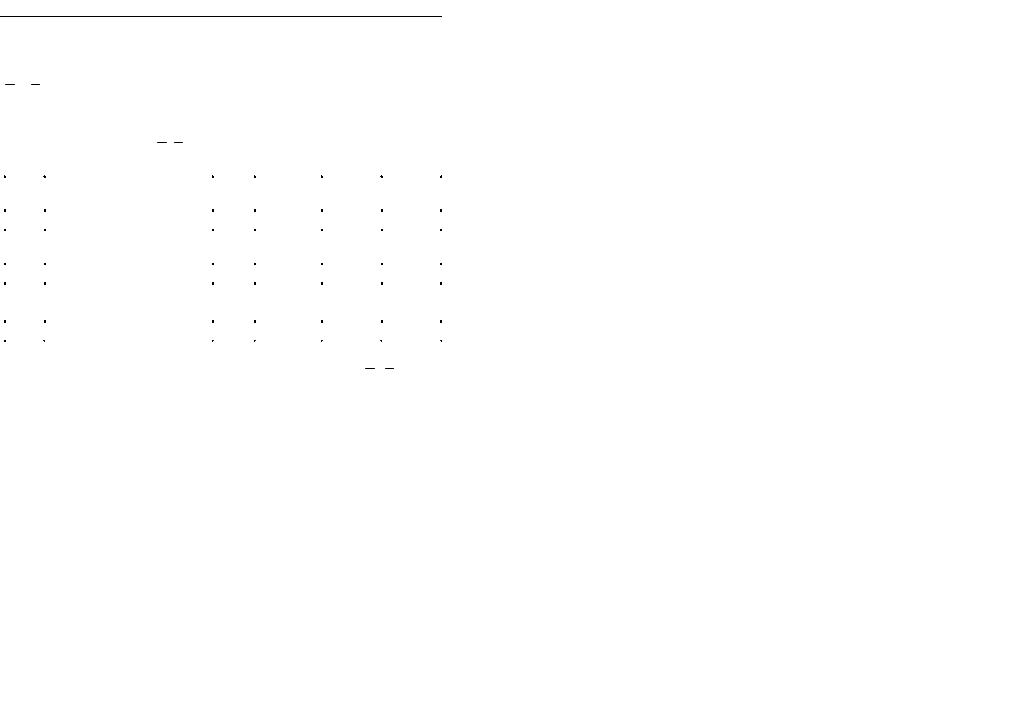
пластинке; при достижении границ последней они должны быть такими, чтобы уравновесить внешние силы, приложенные по контуру. Рассмотрим малую трехгранную призму TSL (рис. 11, в). Ее грань TS совпадаетсграницейпластинки(см.рис.11,а).Проекциинаоси x и y интенсивности поверхностных нагрузок, приложенных к контуру

пластинки,равнысоответственно X иY .Условияравновесиянаконтуре пластинки будут иметь следующий вид (см. рис. 11, в):

где l и m – направляющие косинусы нормали ν к контуру пластинки.

Теория упругости. Часть II

Уравнения (2.1) называютсястатическимиграничнымиусловиями.

Контур пластинки состоит из пяти прямолинейных участков и полуокружности. Значения проекции поверхностных нагрузок

X иY и направляющих косинусов l и m нормалей ν к отдельным

участкам контура пластинки приведены в табл. 2.2.

Таблица 2.2

Значения X,Y , l, m наконтурепластинки

Проекция интенсивности поверхностных нагрузок X (Y ) имеет знак «плюс», если совпадает с положительной осью координат x (y), и знак «минус», если противоположна положительной оси x (y).

Такимобразом,рольграничныхусловийвтеорииупругостизаключается в следующем:

•при помощи статических граничных условий(2.1) обеспечивается равновесие внутренних и внешних сил на поверхности нагруженного тела (см. рис. 11, в);

•при помощи кинематических граничных условий соблюдается совместимость перемещений точек тела в результате деформаций с наложенными на тело связями (см. рис. 11, а);

•при интегрировании дифференциальных уравнений теории упругости появляются постоянные интегрирования (или функции интегрирования), которые определяются из граничных условий.

Задача 3. РЕШЕНИЕ ПРОСТЕЙШИХ ЗАДАЧ В ТЕОРИИ УПРУГОСТИ ОБРАТНЫМ МЕТОДОМ. ОПРЕДЕЛЕНИЕ НАГРУЗОК, ПРИЛОЖЕННЫХ К ТЕЛУ

3.1.Основные уравнения теории упругости

1.Статические уравнения (дифференциальные уравнения равновесия внутри тела – уравнения Навье):

При выводе уравнений (3.1) использованы допущения о сплошности материала и малости деформаций.

2. Геометрические уравнения (соотношения между деформациями и перемещениями – уравнения Коши):

При выводе уравнений (3.2) также использованы допущения о сплошности материала и малости деформаций.

Таккакшесть компонент деформацийвыражаютсятолькочерез три компоненты смешения u, v, w, то деформации не могут быть независимымидруготдруга.Зависимости,выражающиенепрерывность деформаций тела без трещин, – это условия сплошности Сен-Венана в виде шести уравнений совместности деформаций: