Курсовая работа

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный архитектурно-строительный университет»

Строительный факультет

Кафедра прикладной математики и информатики

Курсовая работа по теме:

«Решение краевой задачи методом конечных разностей»

Выполнила:

Студентка группы 7-П-2

Лодочкина А. А.

Санкт-Петербург

2011

Оглавление

1. Теоретическая часть…………………………………………………3

2. Решение, полученное в результате выполнения ручного счета……………………………………………………………………………….4

3. Решение, полученное в результате машинных вычислений…….6

4. Сравнения результатов ручных и машинных вычислений……...11

5. Коэффициенты интерполирующего полинома Лагранжа……..12

6. Коэффициенты линейной и квадратичной аппроксимирующих функций…………………………………………………………………………..13

1. Теоретическая часть

   1. Постановка решаемой задачи

В практике строительных расчетов многие математические модели, используемые для расчета конструкций, приводятся к линейным дифференциальным уравнениям второго порядка, имеющим следующий вид:

y’’ + p(x)y’ + q(x)y = f(x), (1)

где х – параметр, определяющий некоторую координату исследуемого объекта, р(х), q(x), f(x) – заданные функции.

Для решения задачи, определяемой (1), необходимо задать дополнительные условия, определяющие состояние исследуемого объекта при некоторых заданных значениях координатной переменной х. Условия, определяющие состояние объекта в заданных точках х, называются граничными.

Таким образом, для нахождения решения уравнения (1) необходимо определить граничные условия. Например, следующим образом:

y(x₀) = Y₀, y(x_k) = Y_k,

где Y₀, Y_k – фиксированные числовые значения Y₀ и Y_k, определяющие значения исследуемой координаты.

2. Описание метода конечных разностей

Одним из численных методов, применяемых для решения таких уравнений (1), является метод конечных разностей, называемый также методом сеток. Основой этого метода является замена непрерывной области пространства изменения аргумента х на дискретное множество – «сетку» точек x_i, в которых определяются значения y(x_i).

При использовании метода конечных разностей решение задачи осуществляется в результате последовательной реализации четырех этапов:

1. дискретизация области изменения аргументы х;

2. переход от непрерывной дифференциальной математической модели к конечно-разностной модели исследуемого объекта;

3. оформление разностного аналога краевых условий задачи;

4. решение полученное в результате выполнения первых трех шагов математической системы линейных алгебраических уравнений.

2. Решение, полученное в результате выполнения ручного счета

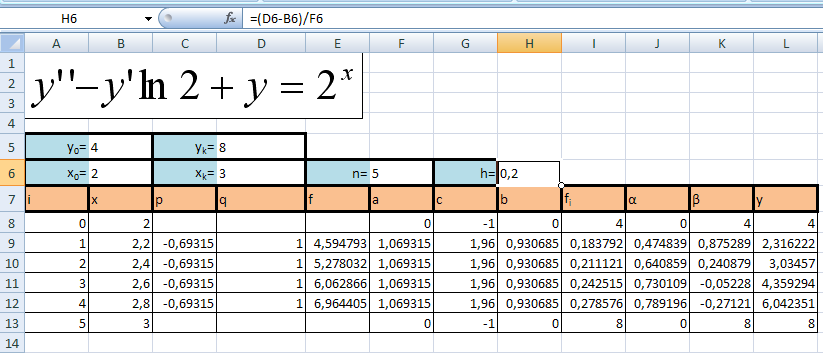
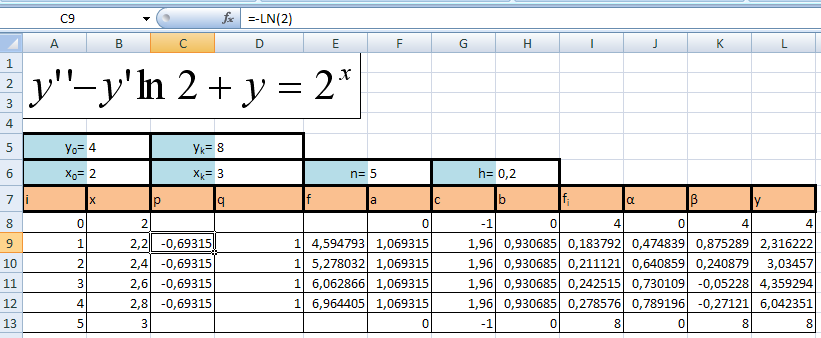
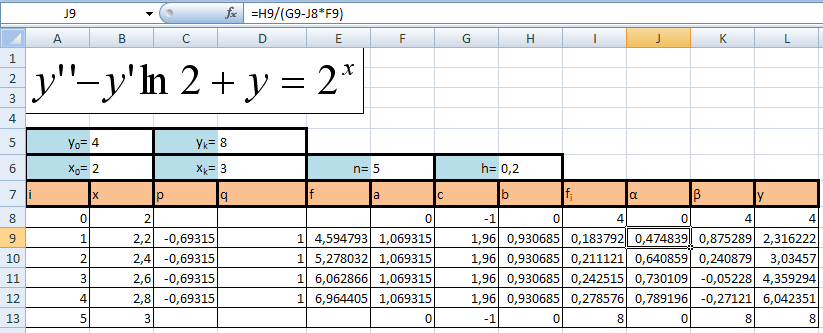
y’’ – y’ln2 + y = 2^x

Y(2)=4; Y(3)=8; n=5

i	x	p	q	f	a	c	b	fi	α	β	y
0	2				0	-1	0	4	0	4	4
1	2,2	-0,693	1	4,594	1,069	1,96	0,931	0,183	0,475	0,876	2,318
2	2,4	-0,693	1	5,278	1,069	1,96	0,931	0,211	0,641	0,241	3,035
3	2,6	-0,693	1	6,063	1,069	1,96	0,931	0,243	0,73	-0,052	4,359
4	2,8	-0,693	1	6,964	1,069	1,96	0,931	0,279	0,789	-0,271	6,042
5	3				0	-1	0	8	0	8	8

1. h=(x_k-x₀)/n; h=0,2;

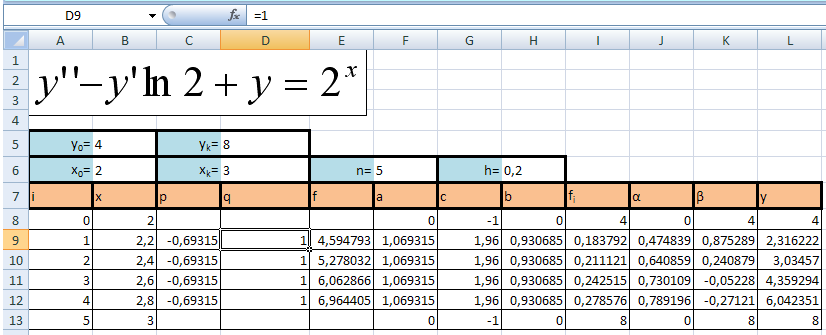
2. x_i=x₀+i*h;

x₀=2

x₁=2+1*0,2=2,2;

x₂=2+2*0,2=2,4;

x₃=2+3*0,2=2,6;

x₄=2+4*0,2=2,8;

x₅=2+5*0,2=3;

p=-ln2=-0,693=const;

q=1=const;

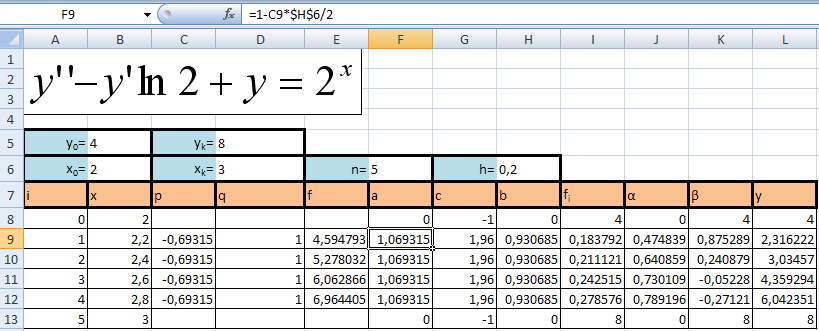
a_i=1-p(x_i)*h/2;

a₀=0;

a₁=1+0,693*0,1=1,069=const=a₂=a₃=a₄;

c_i=2-q(x_i)*h²;

c₀=-1;

c₁=2-1*0,04=1,96=const=c₂=c₃=c₄;

b_i=1+p(x_i)*h/2;

b₀=0;

b₁=1-0,693*0,1=0.931=const=b₂=b₃=b₄;

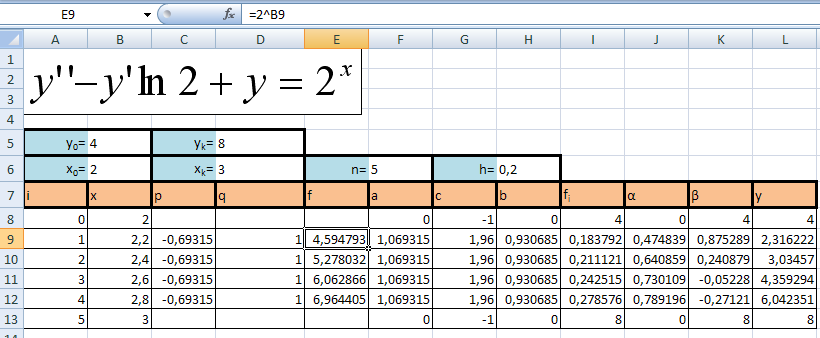
f_i=f(x_i)*h²;

f₀=4;

f₁=4,594*0,04=0,183;

f₂=5,278*0,04=0,211;

f₃=6,063*0,04=0,243;

f₄=6,964*0,04=0,279;

f₅=8;

Y₀ =4

1,069Y₀ +1,96Y₁ +0,931Y₂ =0,183

1,069Y₁ +1,96Y₂ +0,931Y₃ =0,211

1,069Y₂ +1,96Y₃ +0,931Y₄ =0,243

1,069Y₃ +1,96Y₄ +0,931Y₅ =0,279

Y₅ =8

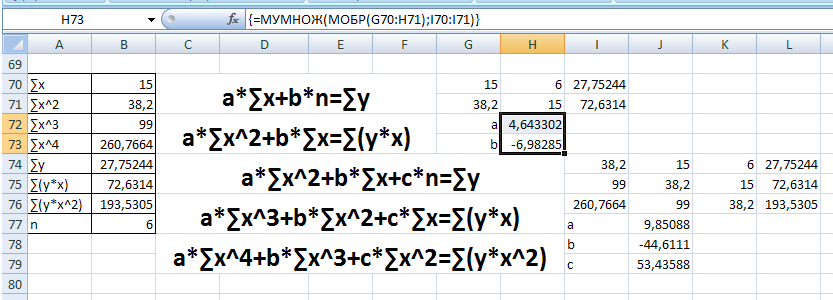
Мы получили линейную алгебраическую систему уравнений с ленточной матрицей. Эффективным методом решения систем уравнений такого типа является метод прогонки.

Получим прогоночные коэффициенты.

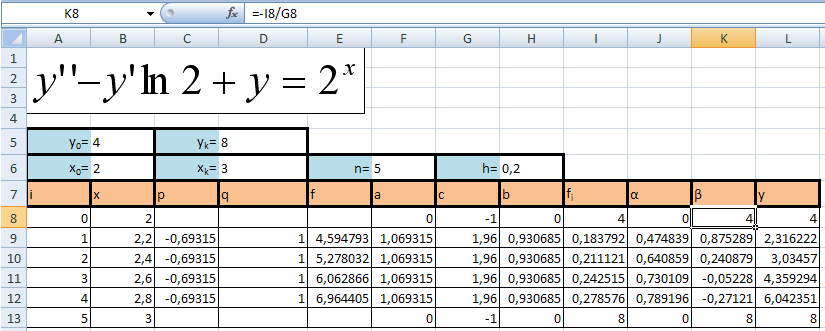
Α₀=b₀ / c₀;

α₀=0/(-1)=0;

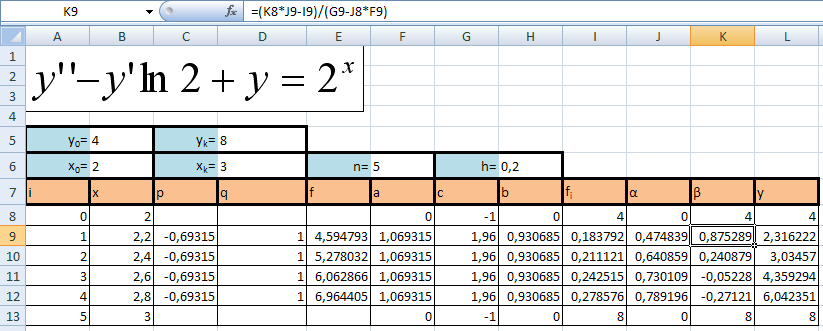
α_i=b_i / (c_i – α₀a_i);

α₁=0,931/(1,96-0*1,069)=0,475;

α₂=0,931/(1,96-0,475*1,069)=0,641;

α₃=0,931/(1,96-0,641*1,069)=0,73;

α₄=0,931/(1,96-0,73*1,069)=0,789;

α₅=0/(-1-0,789*0)=0;

β₀ = -f₀ / c₀;

β₀=-4/(-1)=4

β_i = (β_i-1α_i – f_i) / (c_i – α_i-1a_i);

β₁=(4*0,475-0,183)/(1,96-0*1,069)=0,876;

β₂=(0,876*0,641-0,211)/(1,96-0,475*1,069)=0,241;

β₃=(0,241*0,73-0,243)/(1,96-0,641*1,069)=-0,052;

β₄=(-0,052*0,789-0,279)/(1,96-0,73*1,069)=-0,271;

β₅=(-0,262*0-8)/(-1-0,789*0)=8;

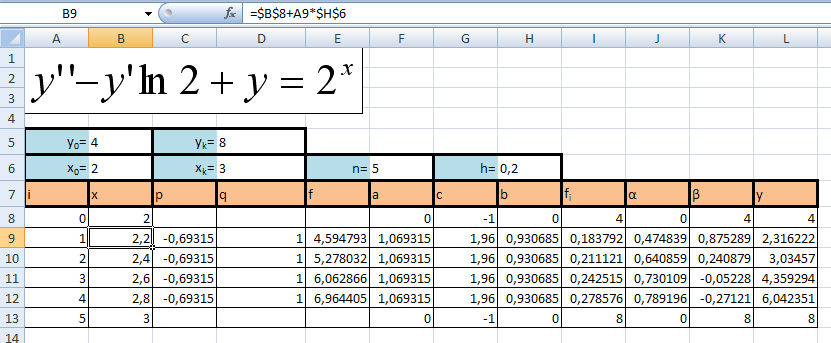
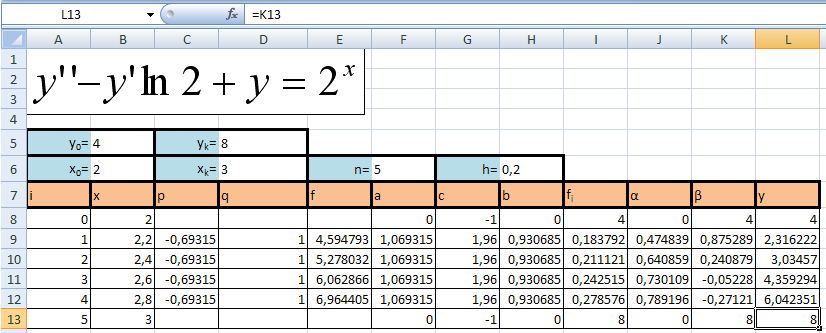
y₅=β₅

y₅=8;

y_i = α_iy_i+1 + β_i;

y₄=0,789*8-0,271=6,042;

y₃=0,73*6,042-0,052=4,359;

y₂=0,641*4,359+0,241=3,035;

y₁=0,475*3,035+0,876=2,318;

y₀=0*(2,318)+4=4.

3. Решение, полученное в результате машинных вычислений

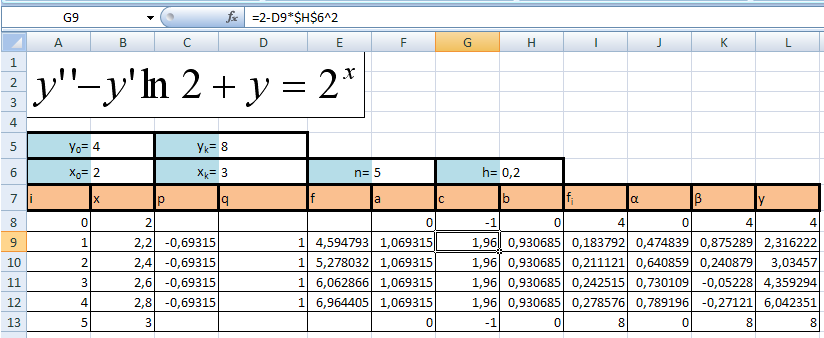
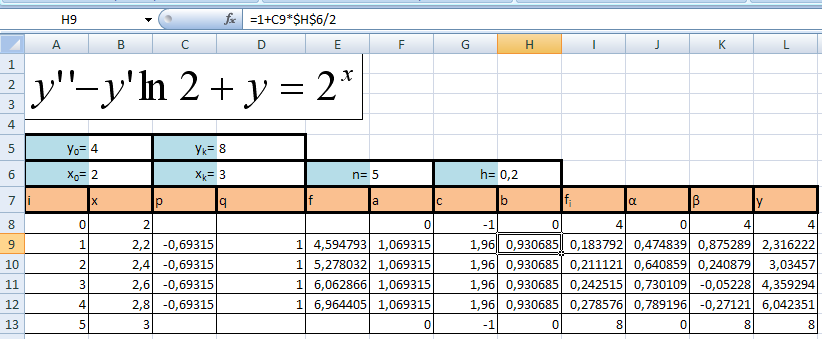
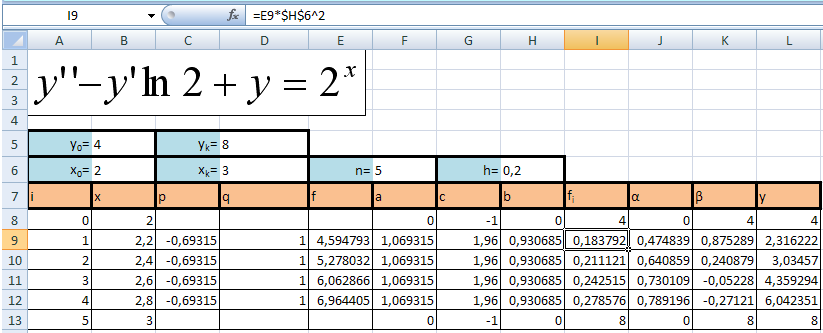
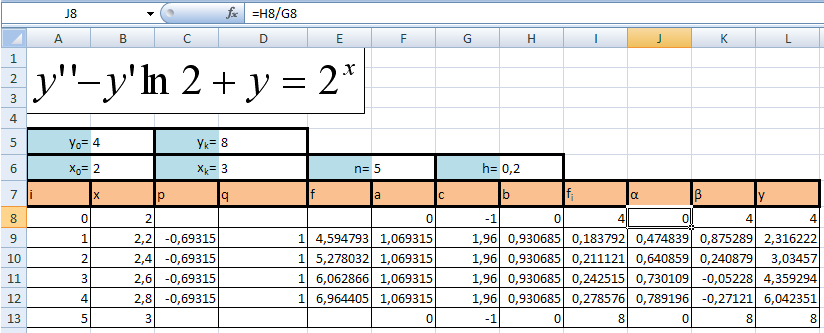
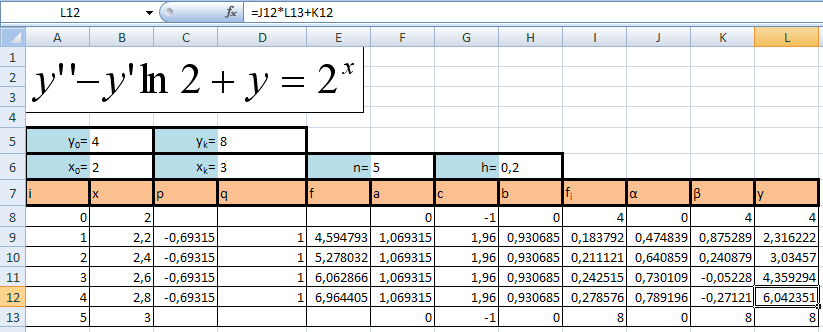
4. Сравнение результатов ручных и машинных вычислений

Результаты, полученные в результате машинного вычисления точнее результатов, полученных в результате ручного счета.

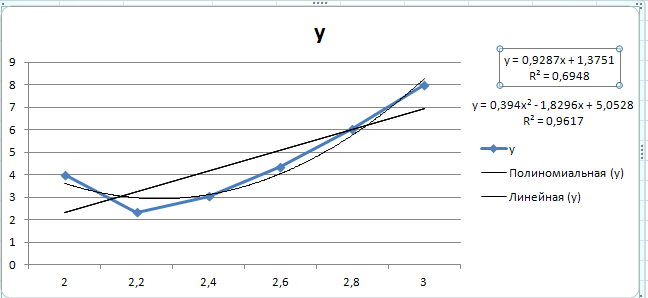
5. Коэффициенты интерполирующего полинома Лагранжа

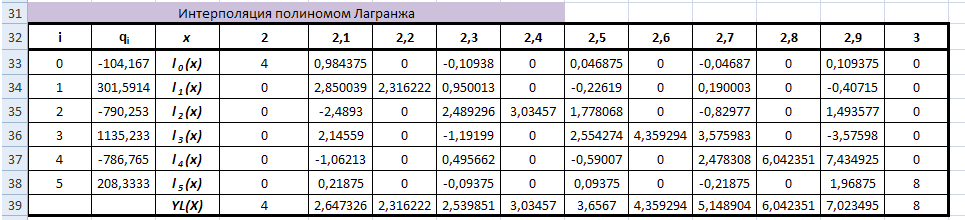
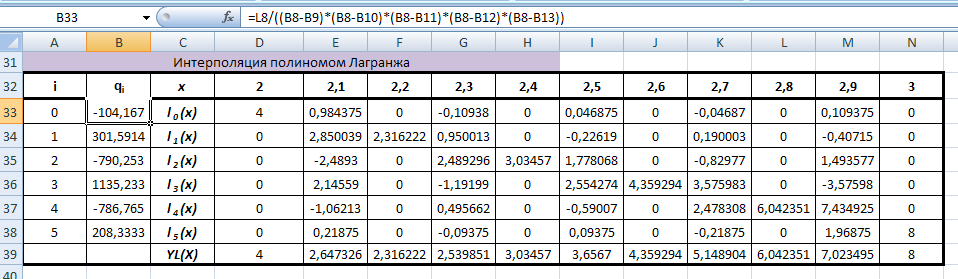
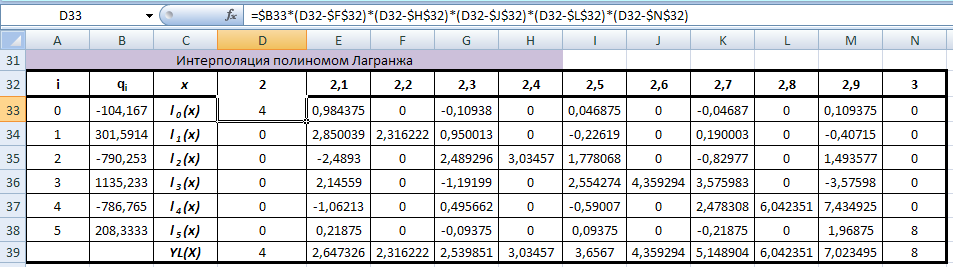
6. Коэффициенты линейной и квадратичной аппроксимирующих функции