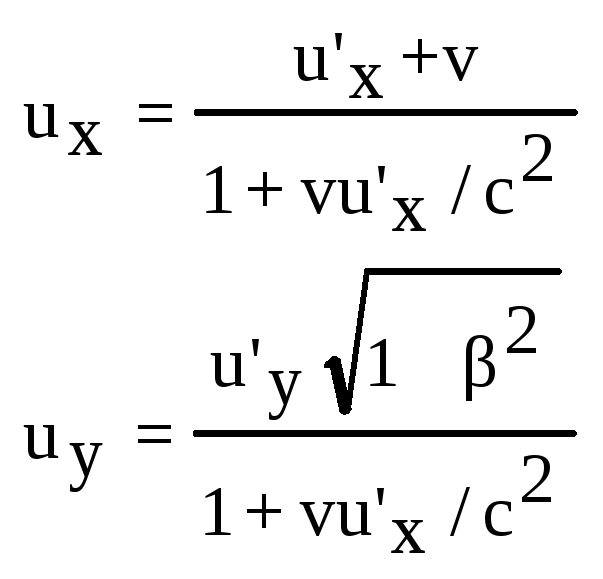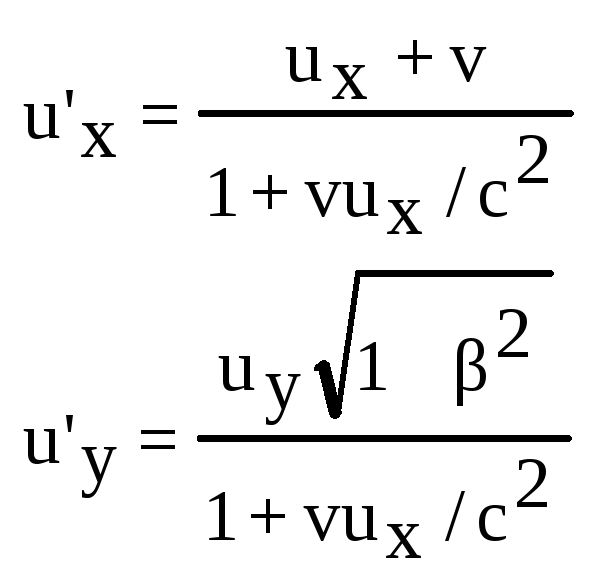Fizika_1_semestr
.doc|
1 |
2-3 |
5-17-21 |
|
Любое движение тела можно представить как совокупность поступательного и вращательного движения. Под материальной точкой понимают не атомы и не молекулы, а микроскопические частицы. Поступательное движение – движение, при котором любая прямая, жестко связанная с телом, остается параллельной своему первоначальному положению. Движение тела проходит в пространстве и времени. Тело отсчета – положение материальной точки относительно другого тела. Система отсчета – совокупность тела отсчета и связанных с ним системой координат и часов.
В Декартовой системе координат положение тела определяется тремя координатами: r = xi + yj + zk, где i, j, k – единичные по модулю и взаимно перпендикулярные векторы – орты системы координат.
При движении материальной точки ее координаты изменяются с течением времени, в общем случае имеем следующее уравнение: х = х (t) y = y (t) r = r (t) z = z (t)
Эти уравнения называются кинематическими движениями материальной точки. Число независимых координат, определяющих положение точки в пространстве, называется числом степеней свободы. |
С Пусть матер. точка движется по какой-то траектории и в момент времени t0 ей соотв. Радиус вектор r0, а в момент времени t0 + t = r, т.е. за время t точка пройдет путь S и получит перемещение r. Вектор средней скорости – отношение вектора перемещения к интервалу времени = r/t. Мгновенная скорость – векторная величина, равная первой производной радиус-вектора движущейся точки по времени. = || = | lim r/t | = lim S/t = dS/dt, = dS/dt Ускорение – физическая величина, характеризующая быстроту изменения скорости по модулю и направлению. Среднее ускорение неравномерного движения в интервале от t до t+t – это векторная величина, равная отношению изменения скорости v к интервалу времени t. a = v/t. Мгновенное ускорение материальной точки в момент времени t есть предел среднего ускорения: a = lim a = lim v/t = dv/dt, при t 0.
Тангенсальная составляющая ускорения: характеризует быстроту изменения скорости по модулю ат = lim a = lim v/t = dv/dt, при t 0.
Нормальная составляющая ускорения: характеризует быстроту изменения скорости по направлении. an = lim vn/t = v2/r
Полное ускорение: a = dv/dt = aт + an. |
При вращательном движении точки лежащая на одном радиусе будут иметь разные линейные скорости, поэтому линейная скорость не может быть характеристикой вращательного движения, такой характеристикой является угол поворота.
T Для характеристики быстроты изменения угла вводят понятие угловой скорости , где = d/dt. Тогда формула для расчета угла поворота будет следующей: = dt.
Перемещение dr можно взять в любом направлении. В частности, вдоль координатных осей X, Y, Z: FX = - dU/dX, FY = - dU/dY, FZ = - dU/dZ. Отсюда легко найти сам вектор F: F = FXi + FYj + FZk, где i, j, k – орты (единичные векторы) декартовых координат. Преобразуем уравнение и получим следующее: F = - (dU/dX i + dU/dY j + dU/dZ k) = - dU. Величину, стоящую в скобках, называют градиентом скалярной функции т обозначают U. U можно рассматривать как произведение символического вектора Набла на скаляр U. И связь между силой поля и потенциальной энергией как функция координат запишется: F = - U. Т.е. сила поля равна со знаком «-» градиенту потенциальной энергии частицы в данный точке поля. |
|
53 |
7 |
8 |
|
Рассмотрим явления, экспериментально подтверждающие основ-ные положения и выводы молекулярно-кинетической теории. Броуновское движение. Наблюдая под микроскопом взвесь цветочной пыльцы в воде, Броун обнаружил, что частицы пыльцы оживленно и беспорядочно двигались. Это движение вызывается ударами молекул среды, в которой частицы взвешены. Так как молекулы движутся хаотически, то броуновские частицы получают толчки с разных сторон, поэтому и совершают движения столь странной формы. Таким образом, броуновское движение является подтверждением выводов молекулярно-кинетической теории о хаотическом (тепловом) движении атомов. Опыт Штерна. Его исследования позволили оценить распределе-ние молекул по скоростям. Схема установки Штерна представляла следующее: вдоль оси внутреннего вращающегося цилиндра натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откаченном воздухе. При этом серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю сторону второго цилиндра, формируя размытое изображение. Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя изображение, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Опыт Ламмерт. Позволил более точно установить скорость движения частиц. Молекулярный пучок должен был пройти через две вращающиеся пластинки с прорезями. Опытно определение постоянной Авогадро. Воспользовавшись идеей распространения молекул по высоте, Перрен эксперимент-ально определил значение пост. Авогадро. Исследуя под микроскопом броуновское движение, он убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. |
1-й закон Ньютона (закон инерции): всякая материальная точка сохраняет свое состояние покоя или равномерное прямолинейное движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. 2-й закон Ньютона: ускорение, приобретаемое материальной точкой, пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки. 3-й закон Ньютона: взякое действие материальных точек друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Поступательное движение – движение, при котором любая прямая, жестко связанная с телом, остается параллельной своему первоначальному положению. Таким образом, за определенное время dt радиусы векторов всех точек поступательно движущегося тела изменяются на одну и туже величину dr. И соответственно скорости и ускорения всех точек должны быть одинаковы. va = vb, aa = ab, v = dr/dt, a = dv/dt.
Поэтому для кинематического описания движения тела достаточно рассмотреть движение одной материальной точки. Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движения.
Вращательное движение – движение, при котором все точки движущегося тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. |
В механике Галилея-Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс.
Центр масс (центр инерции) – воображаемая точка, положение которой характеризует распределение массы этой системы. Импульс системы равен произведению массы системы на скорость ее центра масс (p = mvc).
Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
Для каждого тела механической системы равнодействующая сила будет равна: d/dt (mnvn) = F’n + Fn. Для всех тел системы соответственно: dp/dt = F1 + F2 + … + Fn, где p = mv – импульс системы.
Подставим выражение p = mvc в уравнение dp/dt = F1 + … + Fn.
Закон движения центра масс выглядит так: m dvc/dt = F1 + F2 + … + Fn. |
|
9 |
10-14 |
11-12 |
|
М
Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяем векторным произведением: L = | rp | = | r, m |, где r – радиус вектор из точки О в точку А; p=mv импульс материальной точки. Модуль вектора момента импульса L = r p Sin = m r Sin = p l; - угол между векторами r и p. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
Момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость Lz = Iz . M = dL/dt - основной закон динамики вращательного движения. |
В
Выражение справа – это тендер момента инерции и он характеризует инертные свойства тела при вращении. Т.к. тендер является симметричным, он может быть приведен к диагональному виду. В общем случае, тендер – это упорядоченная совокупность девяти величин, заданная в каждой системе координат.
Момент импульса твердого тела относительно оси – сумма моментов импульса отдельных частиц L = mivi, где v = r L = mivi2 = J, получим L = J. Таким образом, момент импульса тела относительно оси L равен произведению момента инерции тела относительно той же оси на угловую скорость: dL/dt = J d/dt = J = M, следовательно dL/dt = M. Это выражение – есть еще одна форма динамики вращательного движения твердого тела относительно неподвижной оси. Это уравнение (dL/dt = M) известно как уравнение моментов. Закон сохранения момента импульса является фундаментальным законом природы. |
Момент инерции. Опыт показывает, что скорость вращения зависит не только от приложения силы от точки ее приложения, но и от того, как распределена масса относительно оси вращения этот факт и учитывает понятие момент инерции:
Момент инерции является мерой инертности при вращательном движении (чем больше I, тем труднее раскрутить тело). Не всегда тела вращаются вокруг собственной оси.
Так как тело твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно-малый угол d точка проходит путь dS, равный rd и работа равна произведению проекции силы на направление смещения на величину смещения этого смещения: dA = F Sin dS = F Sin r d, т.к. F = Fl = M, имеем: dA = Mzd. Таким образом, работа при вращении тела равна произведению момента силы М относительно данной оси на угол поворота d. Работа при вращении тела ведет на увеличение его кинетической энергии, но: dT = d(Jz2/2) = Jzd, dA = dT, то Jzd = Mzd. При d/dt = получим: M = Jz . Это и есть основное уравнение динамики вращательного движения. |
|
19-22 |
15-23 |
20-28 |
|
Если в каждой точке пространства на помещенную туда частицу действует сила, то говорят, что частица находится в поле сил. Поле, остающееся постоянным во времени, называют стационарным. Стационарное поле в одной системе отсчета может оказаться нестационарным в другой системе отсчета. Работа, которую совершают силы поля при перемещении частицы из точки 1 в 2, зависит от пути между этими точками. В месте с тем, имеются и стационарные силовые поля, в которых работа, совершаемая над частицей силами поля, не зависит от пути между точками. Силы, обладающие такими свойствами, называют консервативными. Это свойство консервативных сил можно сформулировать иначе. Силы поля являются консервативными, если в стационарном случае их работа на любом замкнутом участке равна 0. Все силы, не являющиеся консервативными, называют неконсервативными. Это силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положениями частицы.
Центральная сила – если она направлена к одной и той же точке или от одной и той же точки и зависит лишь от расстояния до этой точки, называемой силовым центром. Примером может служить сила гравитационного притяжения, с которой солнце действует на планету. Или сила электростатического взаимодействия двух точечных зарядов. Центральную силу можно представить: F(r) = f(r)er, где первый сомножитель – зависящий от расстояния, второй – единичный вектор, задающий направление. Центральные силы являются консервативными. |
Пусть частица под действием силы F совершает перемещение по траектории 1-2. В общем случае сила F в процессе движения может меняться как по модулю, так и по направлению. Рассмотрим элементарное перемещение dr, в пределах которого силу F можно считать постоянной. Действие силы F на перемещение dr характеризуется величиной dA, равной скалярному произведению F на dr, которую называют элементарной работой dА силы F. Записать можно так: dA = F dS Cos = FsdS, |dr| = dS. Величина элементарной работы dA является алгебраической величиной и в зависимости от угла может быть положительной или отрицательной. Можно разбить путь 1-2 на бесконечно малые. Если сложить все эти элементарные работы и перейти к пределу, устремив к 0 длины всех элементарных перемещений, а число их к бесконечности, то такой предел обозначается символом: A = FsdS и называется криволинейным интегралом вектора F вдоль траектории 1-2. Элементарная работа двух или нескольких сил равна сумме элементарных работ этих сил: dA = dA1 + dA2.
Измеряя работу консервативных сил, приложенных к системе, можно найти разность значений потенциальной энергии в двух ее состояниях. В каждой конкретной задаче для получения однозначной зависимости энергии от ее конфигурации, выбирают нулевую конфигурацию, в которой потенциальную энергию системы полагают равной 0. Потенциальная энергия механической системы – физическая величина, равная работе, которую совершают все действующие на систему потенциальные силы при переводе системы. Полная механическая энергия системы Е – энергия ее механического движения и взаимодействия, т.е. полная механическая энергия равна сумме кинетической и потенциальной системы. |
Рассмотрим стационарное поле консервативных сил, которым мы перемещаем из разных точек поле в точку O. Т.к. работа сил поля не зависит от пути, то остается ее зависимость от положения точки P при фиксированной точке O. Это значит, что данная работа будет некоторой функцией радиус-вектора r точки P. Обозначив эту функцию U(r), можно записать: АPO = F dr = U(r) – потенциальная энергия частицы в данном поле. Работа на пути 1-0-2 может быть представлена: А12 = F dr = U1 – U2 (убыль потенциальной энергии). Установим связь между потенциальной энергией и силой поля. Точнее, определим поле сил F(r), т.е. силовое поле по заданной потенциальной энергии U(r) как функция положения в поле. Работа может быть представлена как убыль потенциальной энергии или Fdr = - dU. Зная, что скалярное произведение FSdS = - dU, получим: FS = - dU/dS, |dr| = dS. Проекция силы поля F в данной точке на направление перемещения dr равна взятой с обратным знаком производной потенциальной энергии U по данному направлению.
Эйнштейн заложил основы специальной теории относительности. Ее часто называют релятивистской теорией. В основе СТО лежат постулаты Эйнштейна: 1. (Принцип относительности) Никакие опыты (электрические, механические, оптические и т.д.), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнару-жить, покоится ли эта система или движется равномерно и прямо-линейно. Все законы природы инвариантны, т.е. не изменяются при переходе от одной инерциальной системы отсчета к другой. 2. (Принцип инвариантности скорости света) Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. |
|
13-25 |
26-27-29 |
30-33 |
|
Рассмотрим систему материальных точек с массами mi и движущихся со скоростями vi. Пусть Fi’ – равнодействующая внутренних консервативных сил на частицу. Fi – равнодействую-щая внешних сил. При скоростях v < c массы материальных точек постоянны и уравнение 2-го закона Ньютона примет вид: mi dvi/dt = Fi’ + Fi + fi.
Умножим xdri = vidt, получим: m1v1dv1 = (F1’ + F1 + f1)dr1 … mnvndvn = (Fn’ + Fn + fn)drn
Сложим все эти уравнения и получим: d(mivi2/2) = (Fi’ + Fi)dr + fidr.
Это приращение кинетической энергии. Первое слагаемое справа – элементарная работа внутренних и внешних консервативных сил. Второе справа – работа внешних неконсервативных сил, действующих на систему. Т.е. изменение полной механической энергии системы из одного состояния в другое равно работе, совершаемой неконсервативными силами. Таким образом, полная механическая энергия системы сохраняется постоянной. Это выражение представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется. Или другой вариант:: в консервативных системах полная механическая энергия сохраняется, в системах с неконсервативными силами полная энергия не сохраняется. |
В классической механике справедлив механический принцип относительности или принцип относительности Галилея: законы динамики одинаковы во всех инерциальных системах отсчета. Для доказательства рассмотрим 2 системы отсчета: инерциальную систему К с координатами X, Y, Z, которую будем считать неподвижной и систему К’, равномерно и прямолинейно движущуюся со скоростью v = const с координатами X’, Y’, Z’. Отсчет времени начнем с момента, когда начало координат обеих систем совпадают. Если уравнения записать в проекции на оси координат, то увидим: x = x’ + Uxt y = y’ + Uyt z = z’ + Uzt Это и есть преобразования координат Галилея.
Анализ Эйнштейна показал, что классические преобразования Галилея не совместимы с постулатами СТО и должны быть заменены другими преобразованиями. Рассмотрим 2 системы, одна из которых движется с v = const вдоль оси X. За некоторый промежуток времени получим: x – x’ = c (t – t’). Отсчет времени носит относительный характер. В классической механике считается, что время во всех системах течет одинаково. Эйнштейн показал, что преобразования Галилея должны быть заменены преобразованиями Лоренца, удовлетворяющих постулатам Эйнштейна. Они имеют следующий вид: x’ = (x – vt)/(1 - 2) x = (x’ + vt)/(1 - 2) t’ = (t – xv/c2)/(1 - 2) t = (t’ + x’v/c2)/(1 - 2) При v > 0 выражения теряют физический смысл. |
Рассмотрим степень отношения оси x’. Покоящаяся в системе k’ длина стержня l’ = x2’ – x1’, где x2’ и x1’ – не изменяются. Определим длину этого стрежня в системе k, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты начала и конца преобразования Лоренца. Получим следующее: l0’ = x2’ – x1’ = (x2 – x1)/(1 – 2) = l/ (1 – 2), l = (1 – 2) l0’ Длительность события, происходящего в некоторой точке наименьшее в той инерционной системе отсчета, относительно которой эта система неподвижна.
Масса движущихся релятивистских частиц зависит от их скорости: m = m0/(1 – v2/c2), где m0 – масса покоя частицы, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с – скорость света в вакууме; m – масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета. Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон релятивистской динамики материальной точки имеет вид: F = d/dt (m0v/(1 – v2/c2) или F = dp/dt, где p = mv = m0v/(1 – v2/c2) – релятивистский импульс материальной точки. |
|
31-32 |
34-35 |
36-38 |
|
Преобразования Лоренца и следствия из них приводят к выводу об относительности длин и промежутков времени, значение которых в различных системах отсчета разное. В тоже время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов какой-то реальной физической величины, не зависящей от системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям координат. В 4-х мерном пространстве Эйнштейна, в котором каждое событие характеризуется четырьмя координатами (x, y, z, t), такой физической величиной является интервал между двумя событиями: s12 = (c2(t2 – t1)2 – (x2 – x1)2 – (y2 – y1)2 – (z2 – z1)2) Введя обозначение t12 = t2 – t1, получим: s12 = (c2t122 – l122) Обозначив t = t2 – t1 и т.д. и произведя преобразования Лоренца, получим, что (s’12)2 = s122. Отсюда видно, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета.
Рассмотрим движение точки в система К’ (x’, y’, z’), движущейся относительно системы К (x, y, z) со скоростью v = const. Определим скорость этой же точки в системе К. ux = dx/dt, u’x = dx’/dt и т.д. После преобразований Лоренца получим закон (есть еще uz и u’z!):
|
Понятие энтропии введено Клазиусом. Для выяснения физического смысла этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре T теплоотдающего тела, называемое приведенным количеством теплоты, равное в любом обратимом круговом процессе 0. Выглядит так: Q/T = 0. Функция состояния, дифференциалом которой является Q/T, называется энтропией и обозначается S. Из формулы следует, что для обратимых процессов изменение энтропии S = 0. Энтропия системы, совершающей необратимый цикл, возрастает S > 0. Это относится к замкнутым системам. Если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Предыдущие соотношения можно представить в виде неравенства Клаузиуса: S 0, т.е. энтропия замкнутой системы может либо возрастать (в случае необратимости процессов), либо оставаться постоянной (в случае обратимых процеесов).
Используя понятие энтропии и неравенство Клазиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает. И более кратко: в процессах, происходящих в замкнутой системе, энтропия не убывает. Есть еще две формулировки закона: 1. (по Кельвину): невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2. (по Клазиусу): невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретого. |
Основываясь на втором начале термодинамики, Карно вывел теорему: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т1) и холодильников (Т2), наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей (Т1) и холодильников (Т2), равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника. Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно. Порядок цикла 1-2-3-4 по отношению к работе выглядит так: A12 = m/M RT1 lnV2/V1 = Q1 A23 = - m/M Cv(T2 – T1) A34 = m/M RT2 lnV4/V3 = - Q2 A41 = - m/M Cv(T1 – T2) = - A23 Термический КПД цикла Карно определяется так: = (Q1 – Q2)/Q1 или = (T1 – T2)/T1.
Круговой процесс (цикл) – процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой прямой. Если за цикл совершается положительная работа A = pdV > 0, то он прямой, а если отрицательная работа, то он обратный. Цикл применяется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. По 1-му началу термодинамики: Q = U + A = A; = A/Q = 1 – Q2/Q1 (термич. КПД) |

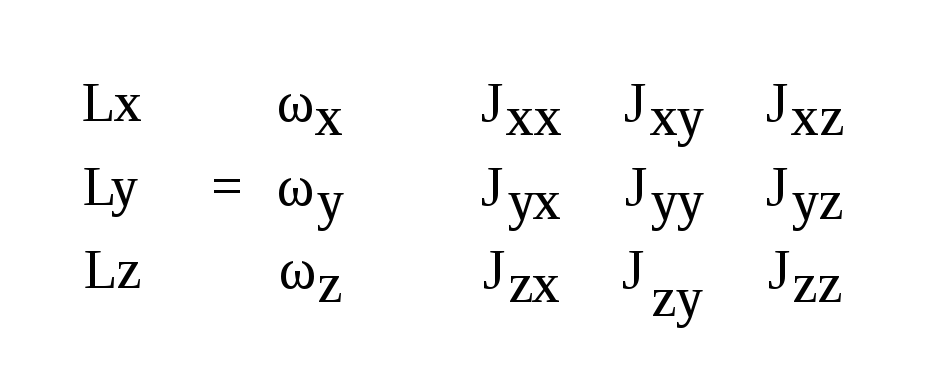 общем случае векторы угловой скорости
и вектор момента импульса не параллельны
и связи между ними не может быть
выражена z
= J.
Если исходить из того, что модули этих
векторов пропорциональны друг другу,
тогда можно записать выражение:
общем случае векторы угловой скорости
и вектор момента импульса не параллельны
и связи между ними не может быть
выражена z
= J.
Если исходить из того, что модули этих
векторов пропорциональны друг другу,
тогда можно записать выражение: