алгебр теория автоматов

Алгебраическая теория автоматов

ПРЕДИСЛОВИЕ

Понятие автомата естественным образом возникает во мно задачах, связанных с вычислительной техникой, управлением, в задачах теории связи и многих других. Математическая структура автомата основывается на интуитивных представлениях о реальных автоматах.

Теория автоматов — развитая математическая теория. К настоящему времени в теории автоматов отчетливо наметились два аспекта. Это комбинаторный аспект и алгебраическая теория. Комбинаторный подход в большей степени связан с поведением, анализом и син автоматов. Оба подхода связаны между собой, и алгебра методы применяются также в комбинаторных задачах; алгебраическая теория автоматов используется в теории языков и алгоритмов. Однако, говоря об алгебраическом аспекте теории автоматов, мы имеем в виду в первую очередь автомат в качестве алгебраической структуры; таким образом, автомат становится объектом алгебраической теории.

Автоматом называется алгебраическая система А с тремя основными множествами А, Х, В и двумя бинарными операциями:

∘ : А ⨯ Х → А; * : А ⨯Х → В.

Здесь А называется множеством состояний автомата, Х — множеством входных сигналов, В — множеством выходных сигналов. Операция ∘ - это функция от двух переменных а ϵ А, х ϵ Х со значениями в множестве состояний А : а ∘ х =ϵ A. Она называется функцией переходов автомата и показывает, как входной сигнал х преобразует состояние a в новое состояние Оперция * - это функция от тех же переменных а ϵ А, х ϵ Х, но со значениями в множестве B выходных сигналов : a * x = b ϵ B. Она называется выходной функцией автомата A и указывает значение сигнала на выходе в зависимости от значения входного сигнала и состояния автомата

В гл. 1 рассматриваются чистые автоматы, т. е. автоматы, множества состояний и выходов которых не наделены никакой дополнительной структурой. Автомат А обозначается следующим образом: А — (А,Х,В, ∘,*) или более кратко А = (А, X, В).

Пусть автомат (А, X, В) элементом x₁ ϵ X переводится из состояния а₁ в состояние а₂ = а₁ ∘ х₁. Если после этого на вход поступает элемент х₂, то он переводит автомат из состояния а₂ в состояние a₂ ∘ х₂ = (а₁ ∘ х₁) ∘ х₂; при этом на выходе автомата появится элемент а₂ * х₂ = (а₁ ∘ х₁)* х₂. Это означает, что последовательное поступление на вход автомата сигналов х₁, х₂ можно рассматривать как новый входной сигнал, который переводит автомат из состояния а₁ в состояние (а₁∘ х₁) ∘ х₂ и дает на выходе сигнал (а₁∘ х₁)*х₂. Естественно считать этот входной сигнал произведением элементов х_хх₂ и рассматривать автоматы, для которых определено ассоциативное умножение входных сигналов. При этом предполагается, что множество входных сигналов есть полугруппа. Обозначим ее Г. Автомат (А, Г, В) называется полугрупповым, если множество его входов является полугруппой, в которой умножение связано с операциями ∘ и * следующими аксиомами:

а∘ 𝜸₁𝜸₂ = (а∘𝜸₁) ∘ 𝜸₂; (П.1)

а*𝜸₁𝜸₂ = (а∘𝜸₁)* 𝜸₁, а ϵ А, 𝜸_i ϵ Г, i=1, 2.

В основном в книге рассматриваются полугрупповые автоматы, и если в тексте нет никаких оговорок, то под автоматом понимается полугрупповой автомат.

Кроме полугрупповых автоматов общего вида (автоматов Мили) изучаются полугрупповые автоматы Мура, характеризующиеся тем, что в них операция * сводится к операции ∘ и некоторому определяющему отображению μ : А⟶В. Существуют различные критерии того, что произвольный автомат является автоматом Мура. Один из них интересен тем, что им выделяется класс полугрупп, являющихся полугруппами входов таких автоматов. Автоматы могут быть избыточны по входам, по выходам, по состояниям. С устранением этой избыточности связано построение трех видов универсальных автоматов.

1. Определения и примеры. Определения автомата и полугруппового автомата были даны в предисловии. Автомат А называется конечным, если конечны его основные множества А, X, В. В ряде случаев приходится рассматривать автоматы, множества А, В которых наделены некоторой алгебраической структурой, например являются линейными пространствами. В этой главе мы ограничимся рассмотрением чистых автоматов, т. е. автоматов, множества состояний и выходов которых не обладают алгебраической структурой. В отличие от полугруппового автомат (А, X, В), у которого множество входов также не наделено алгебраической структурой, будем называть абсолютно чистым.

Чтобы задать автомат, надо задать основные множества и определить действия ∘ и *.

Пример 1. В электро- и радиотехнике известен элемент под названием RS-триггер. Это устройство с двумя входными линиями, на каждую из которых могут подаваться сигналы 0 или 1; устройство может пребывать в двух состояниях: 0 или 1; значения их совпадают со значениями выходного сигнала. Значения входов представляют собой двумерные векторы, координаты которых берутся из множества {0, 1}. В принципе возможны четыре различных входных вектора; в RS-триггере на вход могут подаваться три различных вектора: х₁= (0, 0), х₂ = (0, 1), х₃ = (1, 0). Эти входы действуют на состояния устройства следующим образом: если RS-триггер находился в состоянии 0, то при входах х₁ и х₂ состояний не меняется, а при входе х₃ он переходит в состояние 1; если RS-триггер находился в состоянии 1, то состояние не меняется при входах x₁ и х₃ и переходит в 0 при входе х₂.

Таким образом, RS-триггер — это автомат (А, X, В) с множеством входов X={x₁, х₂, х₃}, множеством состояний А = {а₀, а₁ ; а₀ =0, a₁ = 1} и выходами, идентичными состояниям. Функции переходов и выходов этого автомата совпадают и определяются по следующим правилам:

а₀ ∘х₁ =а_0, а₀ ∘х₂ =а_0, а₀ ∘х₃ =а_1,

а₁ ∘х₁ =а_1, а₁ ∘х₂ =а_0, а₁ ∘х₃ =а_1.

Этот пример интересен тем, что определенный так автомат является одним из блоков, с помощью которых можно сконструировать другие автоматы.

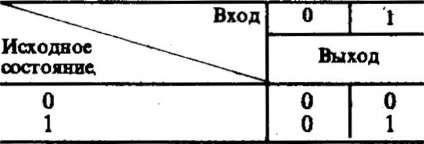
Пример 2. Пусть А = (А, X, В) — автомат с двумя состояни­ями А = {0, 1}, двумя входами Х={0, 1} и двумя выходами B= {0, 1}. Операции ∘ и * задаются по таким правилам:

a ∘x = a+x(mod2), a*x=ax(mod2).

Существуют различные способы задания автоматов: аналитический, табличный, графический и др. В последнем примере операции о и » заданы аналитически. Табличное задание этих операций в данном примере имеет следующий вид:

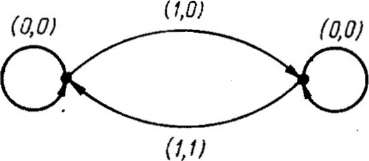
В случае графического описания автомат задается с помощью ориентированного графа, вершинами которого являются состояния а автомата, а ребро, соединяющее вершину а с вершиной а', обозначается парой символов (х, у), где х — входной сигнал, переводящий автомат из состояния а в состояние а', а у — выходной сигнал автомата, равный а *х. Например, граф автомата из последнего примера имеет такой вид:

2. Автоматное представление множества и полугруппы. Пусть А — некоторое множество, S_A — полугруппа всех его преобразо­ваний. Если X — некоторое другое множество, то каждое отоб­ражение f: X⟶ S_A определяет представление элементов из X преобразованиями множества А. Одновременно имеем бинарную операцию ∘ : А⨯ Х⟶ А, определяемую равенством a ∘ x = af(x). Если, кроме того, задана операция о, то каждый х можно трактовать как преобразование множества А и возникает представление f: X⟶ S_A. Указанное соответствие взаимно однозначно. Если Х=Г— полугруппа, то непосредственно проверяется, что соотношение а∘ 𝜸₁𝜸₂ = (а∘𝜸₁) ∘ 𝜸₂; 𝜸_i ϵ Г имеет место тогда и только тогда, когда соответствующее представление f: Г⟶ S_A. есть гомоморфизм. Используя эти рассуждения, определим понятие автоматного представления.

Возьмем автомат А = (А, X, В) и полугруппу S(A, В). Входные элементы х ϵ Х действуют, с одной стороны, как преобразования множества А, т. е. как элементы из S_A, а с другой — как элементы из Fun(A, В). Соответственно этому определим два отображения α : X⟶S_A и β : X⟶Fun(A, В); для каждого х ϵ Х преобразование х^α из S_A и отображение х^β из Fun (А, В) зададим следующим образом: если а ϵ А, то ах^α=а ∘ х, ах^β = а*х.

Далее исходя из автомата А и полагая x^f = (х^α, х^β), определим представление f:X⟶S(A, В). Если X=Г — полугруппа, то легко убедиться, что f:X⟶S(A, В) есть гомоморфизм полугруппы Г в S(A, В).

С другой стороны, пусть имеется отображение f : X⟶S(А, В), и элемент x^f = (φ, ψ) ϵ S(A, B) = S_A ⨯ Fun(A, В) есть образ элемента х. Данному отображению отвечает автомат А = (А, X, В, ∘ , *), в котором а ∘ х =a^φ, а*х= а^ψ. Если Х= Г — полугруппа, то задание гомоморфизма f : Г⟶S(A, В) определяет полугрупповой автомат (А, Г, В) (для доказательства достаточно проверить выполнение аксиом полугруппового автомата).

Таким образом, задание автомата (А, X, В) равносильно заданию представления f: X⟶S(A, В), а задание полугруппового автомата (А, Г, В) равносильно заданию гомоморфизма f: Г⟶S(A, В). Этот гомоморфизм назовем автоматным представлением полугруппы Г.

Абсолютно чистый автомат (А, X, В) называется точным, если отвечающее ему отображение X⟶S(A, В) инъективно; ана­логично, полугрупповой автомат (А, Г, В) точный, если соответ­ствующий гомоморфизм f:Г⟶S(А, В) является мономорфиз­мом — разным элементам из Г отвечают различные элементы в S(A, В). Ядерная конгруэнция р= Кеrf полугруппы Г называет­ся ядром соответствующего автоматного представления или яд­ром автомата А. Каждому автомату А = (А, Г, В) отвечает точный автомат (А, Г/р, В).

3. Гомоморфизмы автоматов. Работу одного автомата можно моделировать работой другого. Математическим понятием, отвечающим физическому понятию моделирования, является гомоморфизм. Приведем его определение. Гомоморфизмом μ :А⟶А' автомата А = (А, X, В) в автомат А' = (А', X', В') называется тройка отображений μ=( μ_1, μ₂, μ₃), μ₁ : А⟶А', μ₂:Х⟶Х',

μ₃ : В⟶В' для которой выполнены следующие условия:

= ∘ ;

= * ; a ϵ A, x ϵ X. (1.1)

Чтобы определить гомоморфизм полугрупповых автоматов μ :(А, Г, В)⟶(А', Г', В'), к условиям (1.1) следует добавить требование:

μ₂ есть гомоморфизм полугруппы Г в полугруппу Г'. (1.2)

Если в последнем определении отображения μ₁, μ₂, μ₃ взаимно однозначны, то μ называется изоморфизмом автоматов. Гомоморфизм (изоморфизм на себя) автомата а в себя называется эндоморфизмом (автоморфизмом) автомата.

Абсолютно чистые автоматы вместе с их гомоморфизмами составляют категорию. Полугрупповые автоматы со своими гомоморфизмами также составляют категорию. Рассмотрим отоб­ражение F, сопоставляющее каждому чистому автомату А полугрупповой автомат F(A). Далее, возьмем произвольный гомоморфизм абсолютно чистых автоматов μ=( μ₁, μ₂, μ₃): А = (А, X, В)⟶А'=(А', X', В') и определим соответствующий ему гомоморфизм полугрупповых автоматов ( , ) = F(μ) : F(A)⟶F(А') следующим образом:= , а в качестве возьмем однозначное продолжение отображения :X⟶X' ⊂F(X') до гомоморфизма : F(X)⟶F(X'). Легко понять, что F(μ) действительно есть гомоморфизм полугрупповых автоматов и что F есть функтор из категории абсолютно чистых автоматов в категорию полугрупповых автоматов.

Предложение 1.1 Всякий гомоморфизм μ=( μ₁, μ₂, μ₃) автомата может быть представлен в виде произведения μ = , гомоморфизмов по выходам , по состояниям и по входам

Гомоморфизмом автомата А = (А, X, В) в автомат А'=(А', X', В') с заменой входных сигналов называется тройка отображений μ₁ : А⟶А', μ₂:Х⟶Х', μ₃ : В⟶В', μ=( μ₁, μ₂, μ₃), удовлетворя­ющая условиям

= ;

= , a ϵ A, x' ϵ X'.

Конгруэнцией автомата А = (А, X, В) называется тройка эквивалентностей: p₁ — на множестве А, р₂ — на множестве X, p_з — на множестве В, p = (p₁, р₂, р₃), удовлетворяющая условию

ap₁a'&хр₂х'=> (а ∘х)р₁(а' ∘ х')&(а*х)р₃ (а'*х'). (1.4)

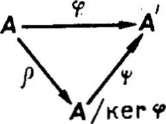
Теорема 1.2 (о гомоморфизмах). Пусть φ - гомоморфизм автомата А на автомат А', τ = ker φ и p — естественный гомоморфизм А на A/ ker φ. Тогда автомат А' изоморфен автомату А/ ker φ , причем существует такой изоморфизм ψ этих автоматов, что произведение рψ равно :

4. Циклические автоматы. Будем рассматривать подавтоматы в заданном полугрупповом автомате А = (А, Г, В). Для подав­томатов имеет место отношение включения А₁ ⊂ А₂, если А₁, есть подавтомат в А ₂. Для любого множества подавтоматов А_α(αϵI) можно рассматривать точную верхнюю и точную нижнюю гран этого набора. Точная нижняя грань есть пересечение подавтомат А_α= (А_α, Г_α , В_α,) = = ().

Точная верхняя грань или объединение автоматов определяется следующим образом: это подавтомат = (), где

— подполугруппа из Г, порожденная всеми Г_α ; — наимен шее инвариантное относительно подмножество из А, содержащее все А_α ; — объединение множества всех элементов В вида а*σ, где а ϵ , σ ϵ Σ и всех множеств В_α , αϵI.

Пусть даны автомат А = (А, Г, В) и тройка множеств (Z, X, Y), Z ⊂ А, X ⊂ Г, Y ⊂ В. Подавтоматом в А, порожденным это тройкой, назовем наименьший подавтомат А' = (А', Г', В') из А для которого Z⊂A', Х⊂Г', Y⊂B'. В свою очередь тройку множеств (Z, X, Y) будем называть системой образующих авто­мата А'. Понятно, что А' равен пересечению всех таких подав­томатов А_α= (А_α, Г_α , B_α ) из А, что Z⊂ А_α, X ⊂ Г_α , Y⊂ В_а.

Следующее предложение описывает автомат, порожденый системой (Z, X, Y).

Предложение 1.4. Если подавтомат А'= (А', Г', В') из (А , Г, В) порожден системой образующих (Z, X, Y), то Г' ecть подполугруппа из Г, порожденная множеством X; множество А есть объединение множества Z с множеством Z∘Г' всех а_∘𝜸, aϵZ, 𝜸ϵ Г'; множество В' — объединение множества Y и множе' с те а всех элементов а*𝜸, аϵ А', 𝜸ϵГ'.