Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Semenova_matem2

.pdf

Скачиваний:

Добавлен:

28.03.2015

Размер:

223.7 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

< 1; z 3 + 2i > 5 2i ; 5 2i = p

= p

25 + 4

3 + 2i

j j j j j

)

) j

3 + 2i >

29:

= p

1 2i

< 1; z 3 + 2i > 1 2i ; 1 2i = p

1 + 4

3 + 2i

)

j j j j j

) j

3 + 2i >

Общая область сходимости — внешность круга jz 3 + 2ij >

29 и

∑

( 1)n ((1

2i)n

+ (5 2i)n)

3 + 2i)n+1

f(z) =

n=0

Таким образом, ряд Лорана для одной и той же функции имеет разный вид для различных колец (областей).

Замечание: при решении воспользовались разложением

1 = 1 z + z2 z3 + : : : + ( 1)nzn + : : : ; jzj < 1: J

1 + z

Задание 9.2. Найдите все лорановские разложения данной функции по степеням z z0:

f(z) =	2z 4	;	z0 = i:
	4z + 8
z2
B Разложим знаменатель на множители:
z2	4z + 8 = 0;
D = 16; z1 = 2 + 2i; z2 = 2 2i:
Функция имеет две особые точки f(z) =				2z 4	:
				(z 2 2i)(z 2 + 2i)

Центр разложения находится в точке z0 = i. Расстояние от точки z0 до

√ √ p z1: (x0 x1)2 + (y0 y1)2 = (0 2)2 + (1 2)2 = 5.

1 z 2 2i

	y
				(III)
	3i
	2i
	(II)
	i	(I)
−3	−2 −1	1	2	3	x
	−i
	−2i
	−3i

Расстояние от				точки	z0 до			z2:
√							.
√							.
(x0 x2)2 + (y0 y2)2					=
	√		2)2 + (1 + 2)2 = p
= (0			2)2 + (1 + 2)2 = p			13
Таким		образом,		существует				три

области, в каждой из которых функция является аналитической и в которых можно построить три сходящихся ряда Лорана (рис.8):

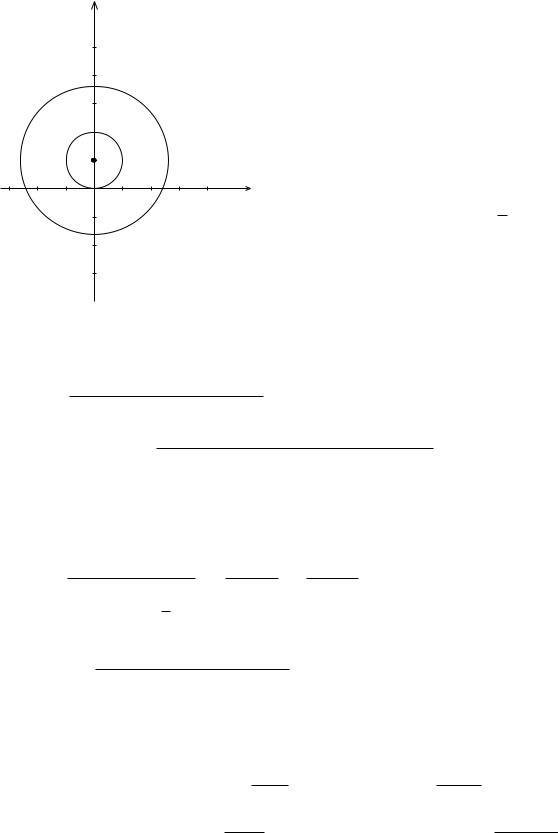
I. Круг jz ij< 5.


p		p
II. Кольцо 5 <jz ij<		13.
	p
III. Вне круга jz ij >		13.

Рис. 8

Рассмотрим все три области. Разложим дробь:


2z 4		=		A	+		B	=
(z 2 2i)(z 2 + 2i)		=	z 2 2i		+	z	2 + 2i	=
(z 2 2i)(z 2 + 2i)			z 2 2i			z	2 + 2i
=	Az 2A + 2Ai + Bz 2B 2Bi						;
=	(z 2 2i)(z 2 + 2i)						;
	(z 2 2i)(z 2 + 2i)

Az 2A + 2Ai + Bz 2B 2Bi = 2z 4; )

z1	A + B = 2
z0	2A(i 1) 2B(1 + i)
Получаем:		2z 4	=
		(z 2 2i)(z 2+2i)

= 4 ) A = 1; B = 1:

+ 1 :

z 2+2i

I. Круг jz ij <

2z 4

(z 2 2i)(z 2 + 2i)

z 2 2i

z 2 + 2i

(z i) i 2

(z i) 2 + 3i

z i

2 + 3i

1 +

z i

2 i

2+3i

( 1)n

z i

( 1)n

z i

n :

∑

(2 + i)

2 + 3i

(

2 + 3i)

n=0

Пронумеруем полученные ряды соответственно (1) и (2).

z i

< 1; z i < 2 + i ; 2 + i = p

1 + 4

= p5

z i < p5:

2 + i

j j

) j j

2 + 3i ; 2 + 3i = p

= p

z i

<1; z i <

4 + 9

2 + 3i

j j j

j j

)

) j

13:

Поэтому общая область сходимости – круг jz ij <

5 и

∑

f(z) = n=0( 1)n (

( 2 + 3i)n+1 (2 + i)n+1 ) (z i)n:

II. Кольцо

5 < jz 3 + 2ij <

13. Ряд (2) в кольце сходится, ряд (1)

расходится, поэтому заменим его другим разложением:

2z 4

(z 2 2i)(z 2 + 2i)

(z i) 2 + 3i

(z i) 2 i

2+i

2 + 3i

1 +

z i

z+3i

2 + i

n +

( 1)n

z i

n ;

∑

i n=0 (z

2 + 3i

n=0

(

2 + 3i)

< 1; jz ij < j2 + ij; j2 + ij= p1 + 4 = p5 ) jz ij < p5:

2 + i

< 1;

i <

2 + 3i ;

2 + 3i

= p4 + 9 = p13

)

2 + 3i

j j

)

i < p

Общая область сходимости – кольцо

5 < jz ij <

13 и

f(z) =

(2 + i)n

( 1)n

(z i)n

∑

i)n+1

∑

n=0 (z

n=0

( 2 + 3i)n+1

III.Кольцо 13 < jz ij < 1: Если пронумеровать полученные ряды аналогично, как и в первом пункте, то видим, что в указанной области первый ряд сходится, а второй – расходится, поэтому заменим

его другим разложением:

2z 4

(z 2 2i)(z 2 + 2i)

(z i) 2

(z i) 2 + 3i

2+i

1 +

2+3i

z i

2 + i n

2 + 3i n

∑

i) + z

) ;

= z 1

i n=0

i n=0( 1)n (

i < 1; jz ij < j2 + ij; j2 + ij = p1 + 4 = p5 ) jz ij < p5:

2 + i

+ 3i

<1; jz ij>j 2 + 3ij; j 2 + 3ij

= 4 + 9 = 13 ) jz ij > 13:

z i

Общая область сходимости:

i >

∑

f(z) =

i)n+1 :

((2 + i)n + ( 1)n( 2 + 3i)n)

n=0

Таким образом, ряд Лорана для одной и той же функции имеет разный вид для различных колец (областей).

Замечание При решении задачи воспользовались разложением:

1	= 1 z + z2 z3 + : : : + ( 1)nzn + : : : ; jzj < 1:
1 + z

1 = 1 + z + z2 + z3 + : : : + zn + : : : ; jzj < 1: J

1 z

Задача 10

Задание 10.1. Данную функцию разложите в ряд Лорана

в окрестности точки z0 f(z) = z sin(

);

z0 = a:

z a

B Пусть z1 = z a, тогда z = z1 + a имеем:

(z1 + a)

+ a

f(z) = f(z1 + a) = (z1 + a) sin

= (z1

+ a) sin

+ a

= (z1 + a) sin( +

) = (z1 + a) sin

( a )2n+1

= (z1 + a)

( 1)

(2n + 1)!

n=0

n 2n+1a2n+1

∑

n 2n+1a2n+1

= z1

( 1)

(2n + 1)! z12n+1

(2n + 1)!

z12n+1

n=0

∑

n+1 2n+1a2n+1

n+1 2n+1a2n+2

( 1)

(2n + 1)!

z12n

(2n + 1)!

z12n+1

n=0

∑

2n+1a2n+1

+ ( 1)n+1

2n+1a2n+2

= n=0

(( 1)n+1 (2n + 1)!

z12n

(2n + 1)!

z12n+1 ) =

∑

= [вернемся к исходной переменной] =

(( 1)n+1

2n+1a2n+1

+ ( 1)n+1

2n+1a2n+2

= n=0

(2n + 1)!

z a2n

(2n + 1)!

z a2n+1 );

∑

для 8z 2 C n fag: J

Задание

10.2. Данную функцию разложите в ряд Лорана в

окрестности точки z0 f(z) = e

z2 6z

(z 3)2

Пусть z

= z

3, тогда z = z

+ 3 имеем:

(z1+3)

+6z1+9 6z1 18

6(z1+3)

f(z) = f(z1 + 3) = e

(z1+3 3)2

= e

z12

= e

z12

= e1

z12

= e e

= ez

= 1

; z

C = e

(

)

[

n=0 n!

8 2

]

n=0

∑

= [8z1 2 C n f0g] = e n=0( 1)n n!9z2n =

∑

= [вернемся к исходной переменной] =

= e

( 1)n

; 8z 2 C n f3g: J

n! (z 3)2n

n=0

∑

Задача 11

Задание 11.1. Определите тип особой точки для данной функции

f(z) =

e 1

ez 1 z

B Разложим числитель и знаменатель функции в ряд Лорана

в окрестности точки z0 = 0, используя известные разложения

ez = 1 +

+ +

+ ; 8z 2 C;

z3n

= 1 +

+ +

+ ; 8z 2 C;

и вычислим предел:

]

f(z) = lim

z!0 ez

(1 +

3! + + n!

+ ) 1

= lim

z!0 (1 + z1!3 + z2!6 + z3!9 + + zn3n! + ) 1 z

z3n 2

= lim

(z + 2! +

3! + +

n! + )

+ +

zn 2

+ )

z!0

(

z3n 2

= lim

z +

2! +

= 0:

z!0

zn 2

Поэтому, в силу леммы 1 п.2.4.3 [5], z0 = 0 — устранимая особая точка. J

Второй способ решения.

B Воспользуемся разложением функции sh z в ряд по степеням z :

z2n+1

sh z =

+ +

+ 8z 2 C;

(2n + 1)!

Тогда:

z2n+1

sh z z = (

+ +

+ ) z =

(2n + 1)!

z2n+1

+ +

+ =

(2n + 1)!

z2n+1

z(2n+1)+1

z2n+3

∑

= n=1 (2n + 1)! = n=1 ((2n + 1) + 1)! = n=1 (2n + 3)! ; 8z 2 C:

Отсюда

f(z) =

1	z2n+3
n=1	(2n+3)!

∑			=
z5
1		2n+3
∑ z

n=1 (2n + 3)!

z2nz3

z2n

∑

(2n + 3)!z5

(2n + 3)!z2

n=1

+ :

3!z2

Так как разложение содержит главную часть, состоящую из одного слагаемого 3!1z2 , то по определению точка z = 0 является полюсом второго порядка.J

Задание 11.2. Определите тип особой точки z = 0 для данной

функции f(z) =

sh z z

B Разложим числитель дроби в ряд Лорана в окрестности точки z = 0,

используя разложение в ряд по степеням z функции sh z.

+ +

z2n+1

8z 2 C;

sh z =

(2n + 1)!

z2n+1

sh z

z +

3! +

5! + +

+ z

lim f(z) = lim

= lim

(2n+1)!

)

z!0 (

[ z3]

z2n+1

5! + +

= lim

(2n+1)!+

z!0

z2n 2

)

= lim z3

z5 =

z!0

(

(2n + 1)!

z2n 2

3! + 5!

+ + (2n+1)!

= lim

z!0

[

]

Таким образом, в силу леммы 2 п. 2.4.3 [5], точка z = 0 – полюс. Установим порядок полюса. Нетрудно заметить, что в данном случае

m = 2. Действительно:

+ +

z2n+1

sh z z

= lim

3! +

lim (z

z )mf(z) = lim z2

(2n+1)!+

z z0

z 0

z2n 2

+ 5! + +

lim

(2n+1)!

(

) =

= z!0

lim

z2n 2

+ + (2n + 1)! + ) = 3! ;

= z!0 (3! + 5!

следовательно, точка z = 0 полюс второго порядка. J

Задача 13

Задание 13.1. Вычислите интеграл

z2 + 1

dz:

(z2

+ 4) sin z

jz Hj

IM z

B В силу теоремы Коши п. 2.5.1 [5]

00000000001111111111

∑

z2 + 1

00000000001111111111

f(z)dz = 2 i

Resf(zk).

00000000001111111111

k=1

00000000001111111111

Для функции f(z) =

00000000001111111111

RE z

+ 4) sin

00000000001111111111

точки z1 = 0; z2 = 2i; z3 = 2i явля-

00000000001111111111

−2i

ются изолированными особыми точ-

ками. Но только z1 = 0 принадлежит

кругу jz 1j2 (рис.9), поэтому

Рис. 9 I

z2 + 1

(z2 + 4) sin z3 dz = 2 iResf(z1):

jz 1j=2

Выясним тип особой точки z1 = 0 :

lim f(z) = lim

z2 + 1

;

(z2 + 4) sin z

z 0

следовательно, в силу леммы 2 п. 2.4.3 [5], z1 = 0 – полюс.

Так как

z2 + 1

lim (z

)f(z) = lim z

= lim

;

(z2+4) sin

(z2

+ 4) sin z

[

]

то

z = 0

– простой полюс. Res

f(z

) = lim (z

z )f(z) =

z2 + 1

lim z

В итоге,

2 i

3 i :

=2 (z2 + 4) sin z dz =

= z

(z2

+ 4) sin z

jz Hj

Задание 13.2. Вычислите интеграл

2 + sin (z 1)

dz:

jz Hj

(z2

3z)

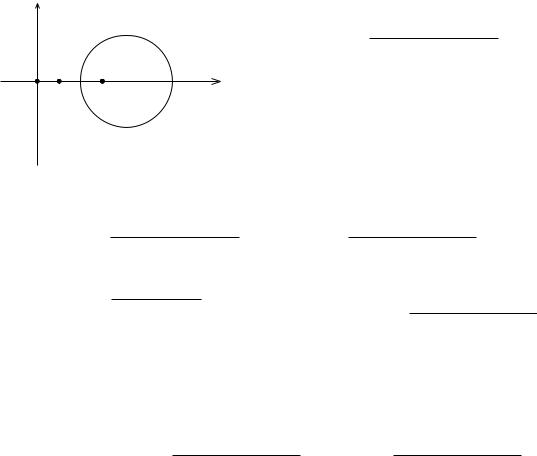
IM z

0000000011111111

1111111100000000

0000000011111111

0 1 200000000111111113 4 RE z

0000000011111111

1111111100000000

0000000011111111

Рис. 10

2 + sin (z 1) dz = (z2 3z)

B Для функции

f(z) = 2 + sin (z 1) , (z2 3z)

точки z1 = 0 и z2 = 3 являются изолированными особыми точками. Только точка z2 = 3 лежит внутри окружности jz 4j = 2 (рис.10).

Перепишем интеграл в ином виде:

2 + sin (z 1) dz = z(z 3)

jz 4j=2						jz 4j=2
	I	2+sin (z 1)						(z	1)
=			z			dz = функция	'(z) =	2 + sin
=		(z		3)		dz = функция	'(z) =	z
z	4 =2				[
j	j

аналитична на области D = z : jz 4j 2: Следовательно,

]

к этой функции применима интегральная формула Коши п. 2.3.4. [5] =

z=3 = 2 i

2 + sin (3

= 2 i'(z2) = 2 i

2 + sin

= 2 i

4 i

2 + sin 2

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.04.2019529.41 Кб2RTsB.doc
#
28.03.20151.02 Mб5rus13.pdf
#
28.03.20151.31 Mб25Ryady_nov.doc
#
28.03.201510.53 Mб109Savin_detali_mash.pdf
#
28.03.2015330.57 Кб36Semenova_matem1.pdf
#
28.03.2015223.7 Кб9Semenova_matem2.pdf
#
07.11.2018410.62 Кб3SERT_LAB.DOC
#
21.09.2019127.03 Кб1shpora.docx
#
28.03.20152.46 Mб3Shpora_1_semestr.doc
#
05.12.2018214.53 Кб8shporki (1).doc
#
24.09.2019484.54 Кб8shporki.docx