
- •Т.А. Павлова дифференциальные уравнения
- •Печатается по решению редакционно- издательского совета ОрелГту Орел 2004
- •302030, Г. Орел, ул. Московская, 65.
- •Введение
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения первого порядка
- •3. Линейные уравнения первого порядка
- •3. 1. Метод вариации произвольной постоянной
- •2). Будем считать произвольную постоянную снеизвестной функциейс(х), т.Е.
- •3. 2. Решение линейных уравнений первого порядка с помощью подстановки
- •4. Уравнение Бернулли
- •5. Уравнения в полных дифференциалах
- •6. Метод изоклин
- •6.1. Геометрические задачи, приводящие к решению дифференциальных уравнений 1-го порядка
- •7. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •7. 1. Первый тип. Уравнения, содержащие только производную порядка n и независимую переменную
- •7. 2. Второй тип. Уравнения, не содержащие искомой функции
- •7. 3. Третий тип. Уравнения, не содержащие независимой переменной
- •8. Линейные дифференциальные уравнения с постоянными коэффициентами
- •8. 1. Метод неопределенных коэффициентов
- •8. 2. Метод вариации произвольных постоянных (метод Лагранжа)
- •9. Литература
3. Линейные уравнения первого порядка
3. 1. Метод вариации произвольной постоянной
Линейным уравнением
первого порядка называется дифференциальное
уравнение первого порядка линейное
относительно yи![]() т.е.
т.е.
![]() (3)
(3)
1).Если в (3) Q(x)=0, то (3)называется однородным:
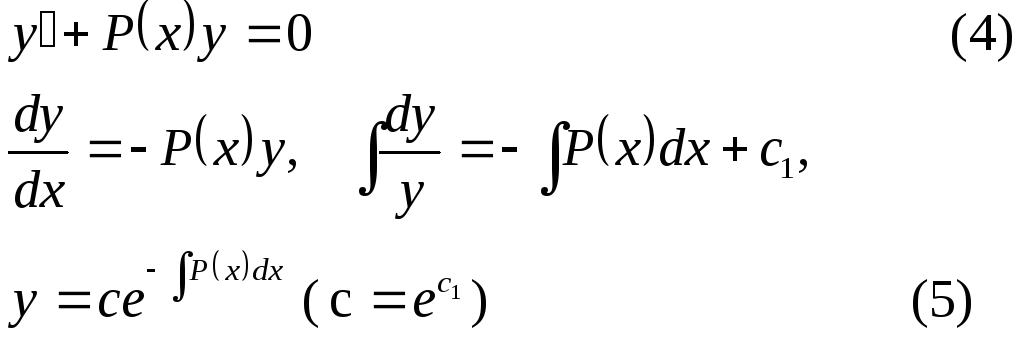
Уравнение (5) является общим решением уравнения (4).
2). Будем считать произвольную постоянную снеизвестной функциейс(х), т.Е.
Полученные выражения для yиy/подставим в (3) и найдемс (х):
Решение уравнения (3) запишется в виде (подставим в (5))
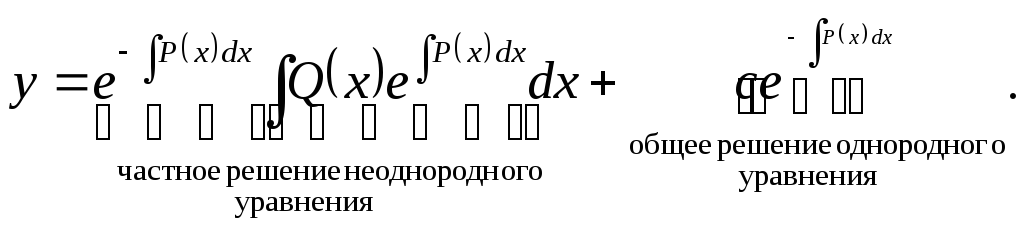
Рассмотренный способ называется методом вариации произвольной постоянной.
3. 2. Решение линейных уравнений первого порядка с помощью подстановки
Уравнение
(3) можно решить с помощью подстановки:
y=UV,
где U=U(x),
V=V(x).
Тогда
![]() .
.
Подставим
![]() и
и![]() в (3):
в (3):
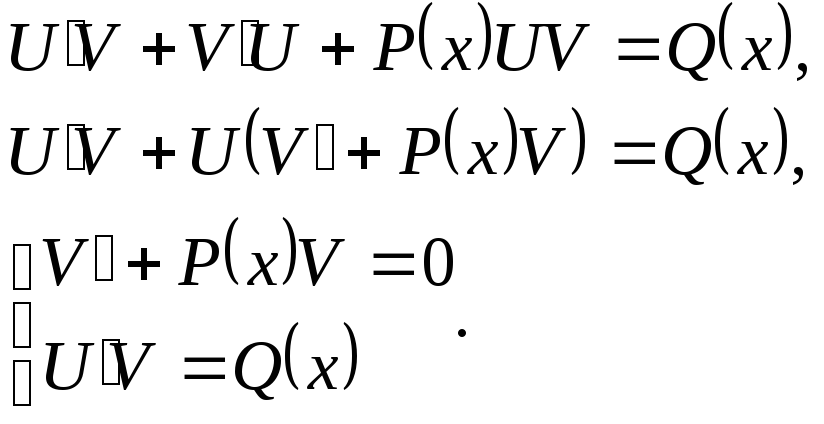
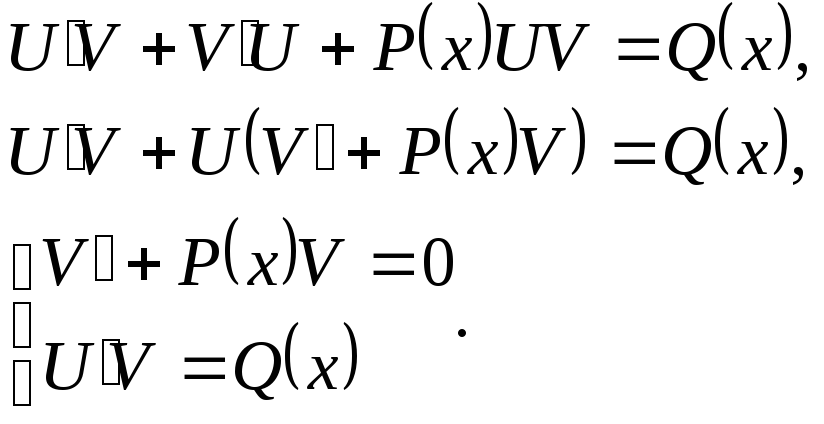
Во многих примерах необходимо решить задачу Коши (например, в задачах №4, №5, №6, №11).Процесс решения сводится к отысканию частного интеграла дифференциального уравнения n-го порядка (n=1,2,3,...), удовлетворяющего n начальным условиям вида
![]() .
.
![]() .
.
Т.е. ищут общее решение дифференциального уравнения, а затем, воспользовавшись начальными условиями, находят значения всех n произвольных постоянных c1, c2,..., cn, входящих в общий интеграл уравнения.
Задача №4. Найти решение задачи Коши:
4.31
![]() .
.
Решение. Перед нами линейное дифференциальное уравнение 1-го порядка. Решим его двумя способами.
I-способ.
Решение уравнения ищется в виде
произведения двух функций U=U(X)
и V=V(X),
т.е. y=UV,
одна из которых выбирается произвольным
образом;
![]() .
Подставляя в исходное уравнение, получим
.
Подставляя в исходное уравнение, получим
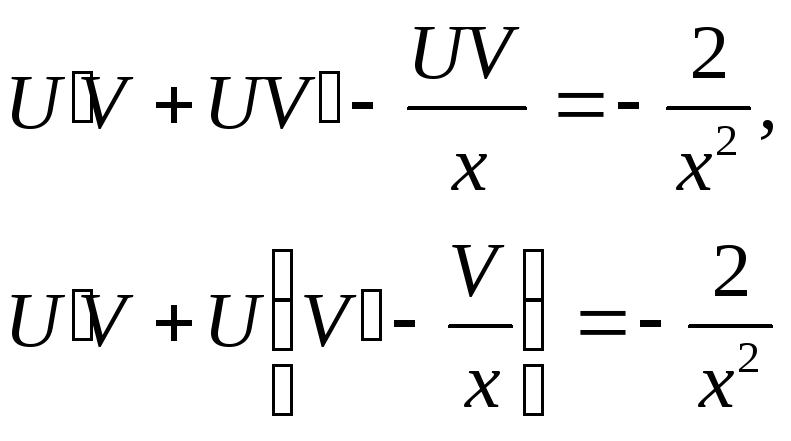 .
.
Исходя из того, что одну из функций ищут произвольным образом, полученное уравнение разбивают на два следующим способом:
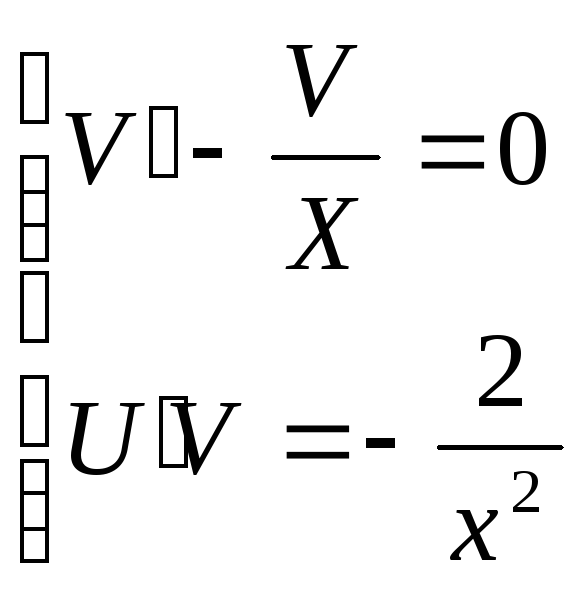 .
.
Выпишем первое уравнение из системы и решим его:

Мы
можем воспользоваться частным случаем
функции V,
например, когда c=1,
V=x
(значение для c
берут таким образом, чтобы функция V
не оказалась тождественно равной нулю,
в противном случае невозможно будет
искать функцию U).
Подставим найденное значение для V
во второе уравнение системы и найдем
функцию U:
![]() .
.
Следовательно,
функция
![]() .
Таким образом, найдено общее решение
исходного уравнения. Подставляя начальное
условие, найдемc:
c=0.
.
Таким образом, найдено общее решение
исходного уравнения. Подставляя начальное
условие, найдемc:
c=0.
Т.е.
решением задачи Коши, удовлетворяющем
данному начальному условию является
![]() ,
что и будет ответом.
,
что и будет ответом.
II-способ. Метод вариации произвольной постоянной.
Составим и решим соответствующее однородное уравнение:
![]() .
.
Теперь
предположим, что константа c
является функцией от переменной x,
т.е. c=c(x),
тогда y=xc(x).
Найдем
![]() и
подставим в исходное уравнение:
и
подставим в исходное уравнение:
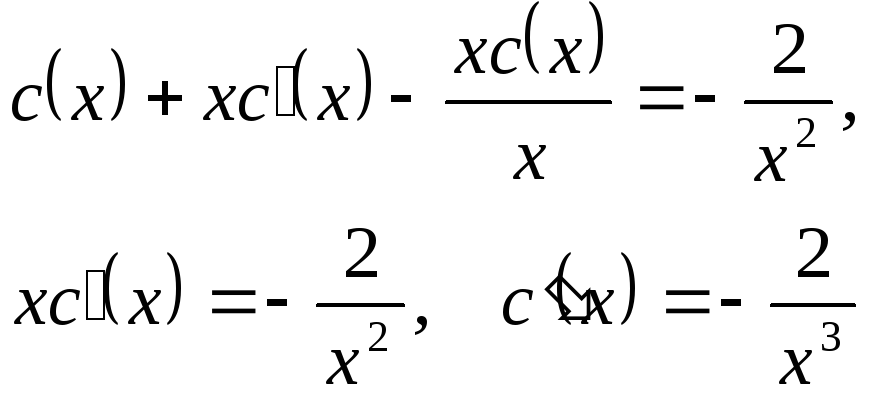 .
.
Интегрируя обе части уравнения, получим
![]() .
.
Тогда
![]() - общее решение исходного дифференциального
уравнения. Подставляя начальное условие,
найдем, чтоc=0
и
- общее решение исходного дифференциального
уравнения. Подставляя начальное условие,
найдем, чтоc=0
и
![]() - частное решение.
- частное решение.
Задача №5 .Решить задачу Коши
![]()
Решение. Так же как и в задаче №4 это линейное уравнение 1-го порядка, если рассматривать x как функцию от y. Преобразуем уравнение:
![]()
Решим его методом вариации произвольной постоянной.
1)
![]()
2)
![]()
3)
![]()
Подставляя 2) и 3) в исходное уравнение, получим
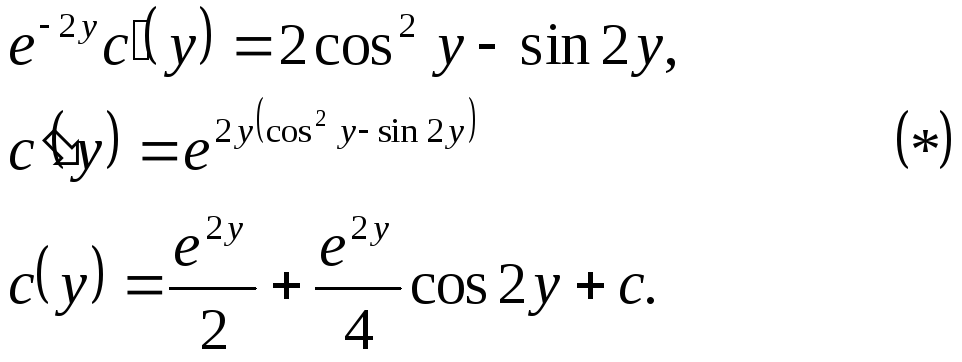
(Интегрировать уравнение (*) удобнее, если преобразовать правую часть, воспользовавшись тригонометрическими формулами.)
Тогда
![]()
- общее решение исходного уравнения.
Подставляя начальное условие, найдем, что c=-2. Тогда решением задачи Коши будет
![]()
