
Примеры для самостоятельной работы
Вычислить повторные интегралы в полярных координатах:
32.
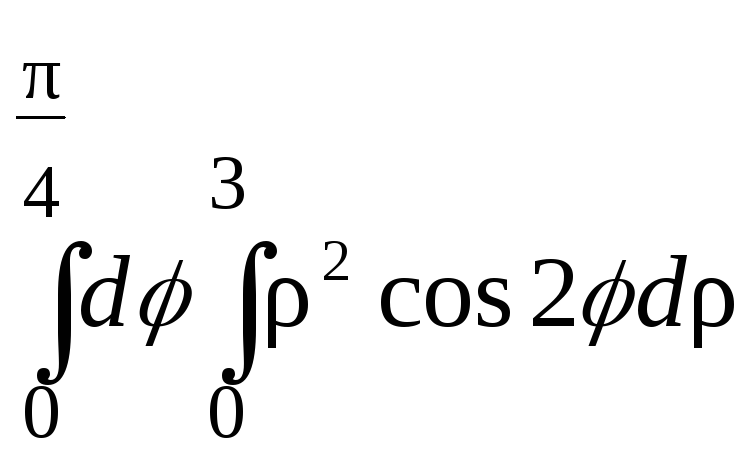 ;33.
;33.
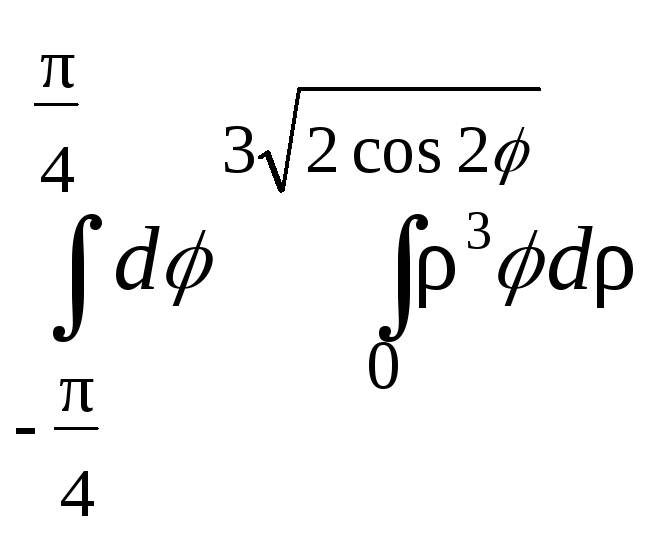 ;34.
;34.
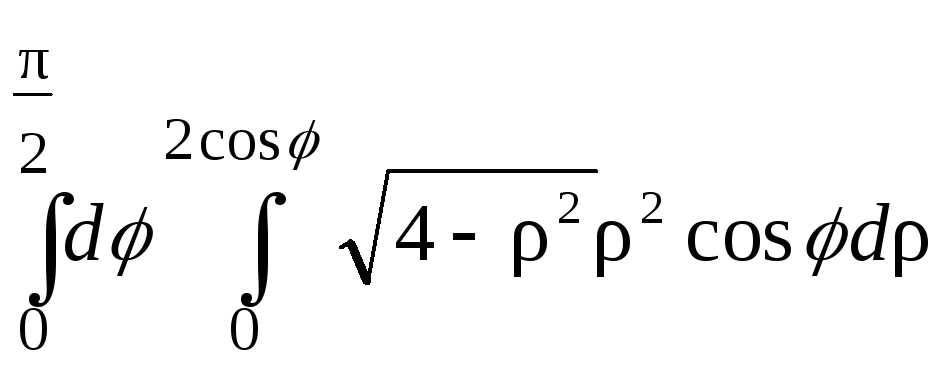 .
.
Вычислить двойные интегралы в полярных координатах по указанным областям:
35.
![]() ,
где область
определена
неравенствами
,
где область
определена
неравенствами
![]() ,
,![]() ;
;
36.
![]() ,
где область
ограничена
линиями
= 1,
= 2 + cos,
полярной осью и расположена выше полярной
оси;
,
где область
ограничена
линиями
= 1,
= 2 + cos,
полярной осью и расположена выше полярной
оси;
37.
![]() ,
где область
ограничена полярной осью, линией
,
где область
ограничена полярной осью, линией
![]() и расположена выше полярной оси.
и расположена выше полярной оси.
Расставить пределы интегрирования в двойных интегралах по указанным областям:
38. Область ограничена окружностями = R, = 2R cos и находится выше первой окружности;
39. Область ограничена линиями = 1, = 2 + cos.
В
двойном интеграле
![]() перейти к полярным координатам, положивх =
cos,
у
=
sin,
и расставить пределы интегрирования в
случае указанных областей D:
перейти к полярным координатам, положивх =
cos,
у
=
sin,
и расставить пределы интегрирования в
случае указанных областей D:
40.
Область D
ограничена линиями х2
+ у2
= 1, х2
+ у2
= 4, у
= х,
![]() ;
;
41. Область D ограничена линией х2 + у2 = 2Rу;
42. Область D ограничена линией (х2 + у2)2 = 4(х2 – у2).
Переменить порядок интегрирования в следующих интегралах, заданных в полярных координатах:
43.
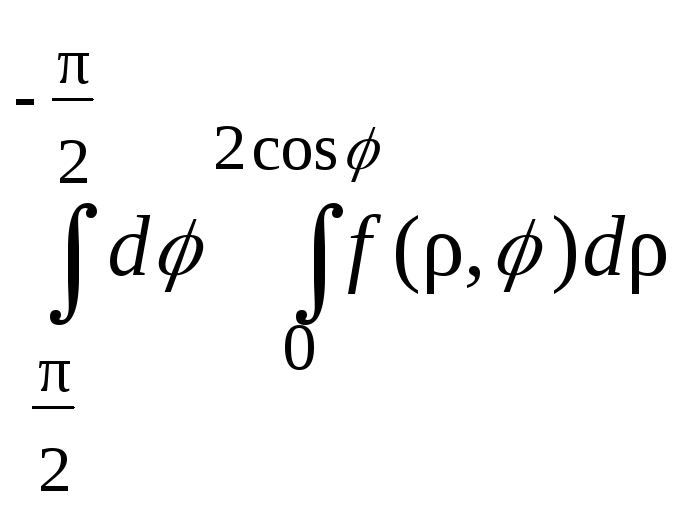 ;44.
;44.
 ;45.
;45.
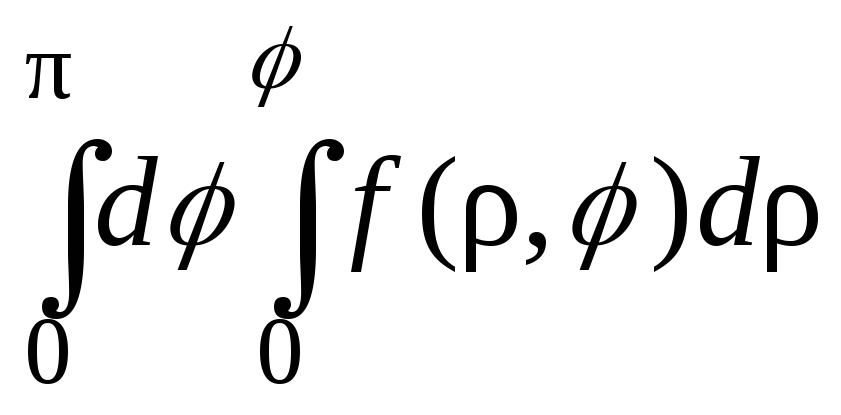 .
.
Вычислить двойные интегралы, введя полярные координаты:
45.![]() ,
гдеD
ограничена линиями х2
+ у2
= 4, х2
+ у2
= 16 (х
0, у
0);
,
гдеD
ограничена линиями х2
+ у2
= 4, х2
+ у2
= 16 (х
0, у
0);
46.![]() ,
гдеD
определена неравенствами х2
+ у2
2Rx
(у
0);
,
гдеD
определена неравенствами х2
+ у2
2Rx
(у
0);
47.![]() ,
гдеD
– круг х2
+ у2
16;
,
гдеD
– круг х2
+ у2
16;
48.![]() ,
гдеD
ограничена линиями (х2
+ у2)2
= 4(х2
- у2),
y = 0,(х
> 0, у
> 0);
,
гдеD
ограничена линиями (х2
+ у2)2
= 4(х2
- у2),
y = 0,(х
> 0, у
> 0);
49.![]() ,
гдеD
ограничена линией (х2
+ у2)
= 2ху;
,
гдеD
ограничена линией (х2
+ у2)
= 2ху;
50.
Вычислить
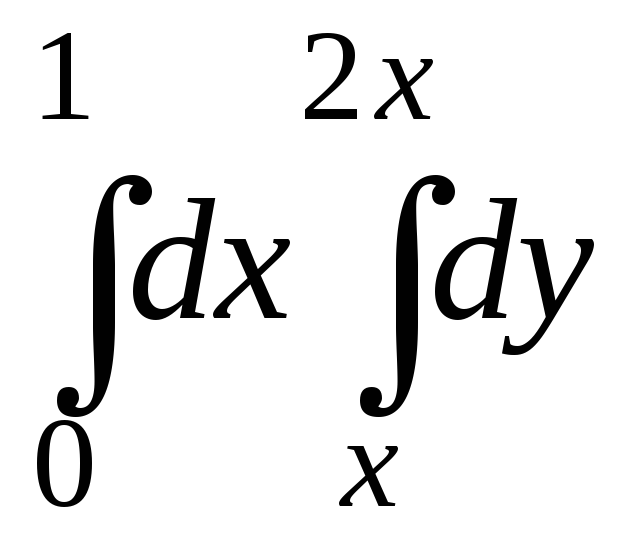 ,
введя новые переменныеx
= u(1
- v),
y
= uv;
,
введя новые переменныеx
= u(1
- v),
y
= uv;
51.
Вычислить
![]() ,
если областьD
ограничена линиями ху
= 1, ху
= 2, у = х,
у = 3х
(произвести замену переменных
,
если областьD
ограничена линиями ху
= 1, ху
= 2, у = х,
у = 3х
(произвести замену переменных
![]() ,
,![]() ).
).
1.3. Несобственные двойные интегралы
Интегралы, распространенные на неограниченную область. Рассмотрим функцию f(x, y), определенную в неограниченной области D. Предположим, что эта функция интегрируема в любой части D’ области D, т.е. существует двойной интеграл
![]() .
(17)
.
(17)
Кривую , отсекающую область D’, всеми ее точками станем удалять в бесконечность так, чтобы наименьшее расстояние R ее точек до начала координат неограниченно возрастало, а отсекаемая ею переменная область D’ постепенно охватывала все точки области D.
Несобственным интегралом от функции f(x, y) в неограниченной области D называется предел (конечный или бесконечный) интеграла (17) при R :
![]() .
(18)
.
(18)
В случае существования конечного предела интеграл (18) называется сходящимся, в противном случае – расходящимся. Функция, для которой интеграл (18) сходится, называется интегрируемой (в несобственном смысле) в области D.
Пусть
далее функция f(x,
y)
задана в неограниченной области любого
вида. Полагая ее равной нулю вне этой
области, всегда можно свести дело к
случаю неограниченной прямоугольной
области – одному из прямоугольников:
![]() ,
,![]() ,
,![]() или к сумме некоторых из этих
прямоугольников.
или к сумме некоторых из этих
прямоугольников.
Если
в каждом конечном прямоугольнике
![]() (при любыхb
> a,
d
> c)
существует в собственном смысле двойной
интеграл от данной неотрицательной
функции f(x,
y)
и простой интеграл по у,
то
(при любыхb
> a,
d
> c)
существует в собственном смысле двойной
интеграл от данной неотрицательной
функции f(x,
y)
и простой интеграл по у,
то
![]() ,
,
![]() ,
(19)
,
(19)
где
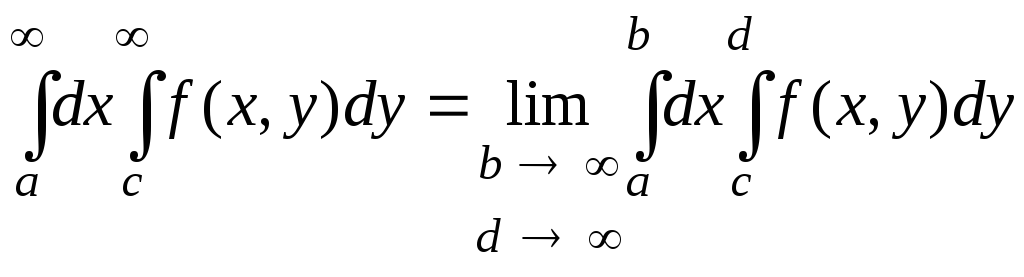 ,
(20)
,
(20)
в предположении, что повторный интеграл сходится.
Если
функция f(x,
y)
меняет знак в бесконечной области D,
формула (19) верна при дополнительном
условии сходимости повторного интеграла
от абсолютной величины данной функции:
![]() .
.
Двойные интегралы от неограниченных функций. Пусть функция f(x, y) задана в ограниченной области D, но оказывается неограниченной в окрестности некоторой точки М(х, у), а в любой части области D, не содержащей этой точки, она является интегрируемой в собственном смысле.
Выделим особую точку М, окружив ее кривой . Если удалить из области D окрестность, имеющую площадь и ограниченную кривой , получим область D’, для которой существует двойной интеграл (17). Станем «стягивать» кривую в точку М так, чтобы диаметр d области, ограниченной , стремился к нулю.
Несобственным интегралом от неограниченной функции f(x, y) по области D называется предел интеграла (17) при d 0:
![]() .
(21)
.
(21)
Если указанный предел существует и конечен, интеграл (21) называется сходящимся, в противном случае – расходящимся.
Аналогично определяется несобственный интеграл в случае, когда имеется несколько отдельных особых точек или указанные точки заполняют особую линию.
Замена
переменных в несобственных двойных
интегралах.
В плоскости Оху
и Ouv
рассмотрим ограниченные области D
и ,
связанные формулами преобразования
![]() ,
,![]() или обратными им
или обратными им![]() ,
,![]() ,
с соблюдением оговоренных ранее условий
(см. формулы (12) и (13)).
,
с соблюдением оговоренных ранее условий
(см. формулы (12) и (13)).
Пусть в области D задана функция f(x, y), непрерывная всюду, за исключением конечного числа отдельных точек или кривых, где она обращается в бесконечность. В этом случае выполняется равенство
![]() ,
(22)
,
(22)
если сходится один из этих интегралов (сходимость другого следует отсюда).
Формула (22) верна и для случая неограниченных областей. Замена переменных, наряду с переходом к повторному интегралу, является удобным средством для установления сходимости несобственных двойных интегралов.
Пример
20. Исследовать,
сходится ли двойной интеграл
![]() ,
где областьD
определена неравенствами х
1, ух
1.
,
где областьD
определена неравенствами х
1, ух
1.
Данный двойной интеграл является несобственным, поскольку область интегрирования – бесконечная часть первого квадрат, ограниченная слева прямой х = 1 и снизу гиперболой ху = 1 (рис. 35).
Рассмотрим
конечную часть области D
– область D’,
ограниченную линиями х
= 1, х = b,
![]() ,y
= d
(рис. 36, область MDAB).В
области D’
двойной интеграл существует в собственном
смысле (при любых b
> 1, d
> 1):
,y
= d
(рис. 36, область MDAB).В
области D’
двойной интеграл существует в собственном
смысле (при любых b
> 1, d
> 1):
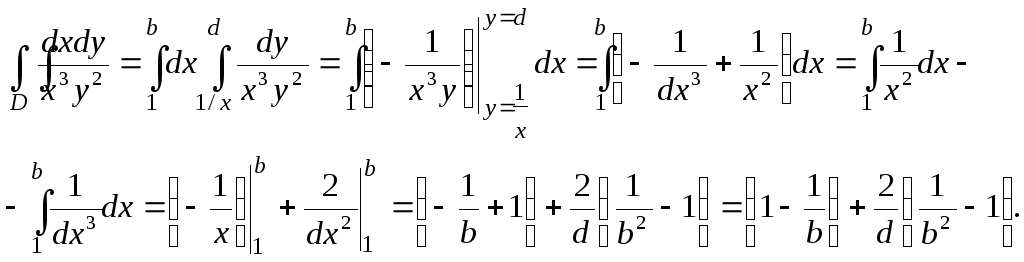
y
у
d M D















D
D’
A
B
0
х
0
1 b
x

Рис. 35
Рис. 36
Поскольку подынтегральная функция положительна во всей области D, то в соответствии с формулами (19) и (20)
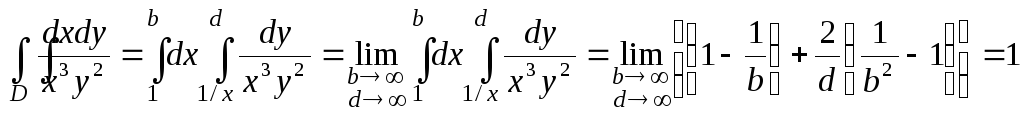 .
.
Следовательно, данный несобственный двойной интеграл сходится и равен единице.
Пример
21. Исследовать,
сходится ли
![]() ,
гдеD
– круг
,
гдеD
– круг
![]() .
.
Данный
двойной интеграл является несобственным,
поскольку подынтегральная функция не
ограничена в данной области (на границе
области, т.е. на окружности
![]() ,
она обращается в бесконечность).
,
она обращается в бесконечность).
Для решения вопроса о сходимости интеграла перейдем к полярным координатам по формулам х = cos, y = sin:
![]() ,
,
![]() ;
;
пределы
интегрирования:
= 0,
= 2,
![]() ,
,![]() .
.
Формула (22) в данном случае примет вид
![]() .
.
Так как
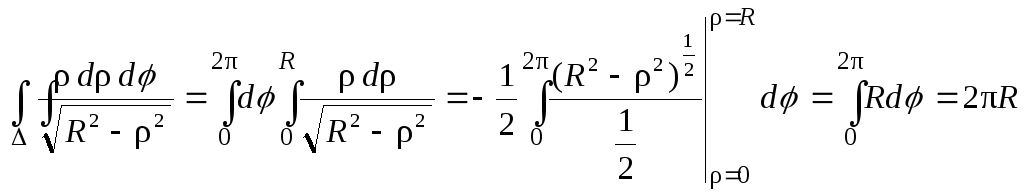 ,
,
то
![]() ,
,
т.е. двойной несобственный интеграл сходится и равен 2R.
Пример
22. Исследовать,
сходится ли
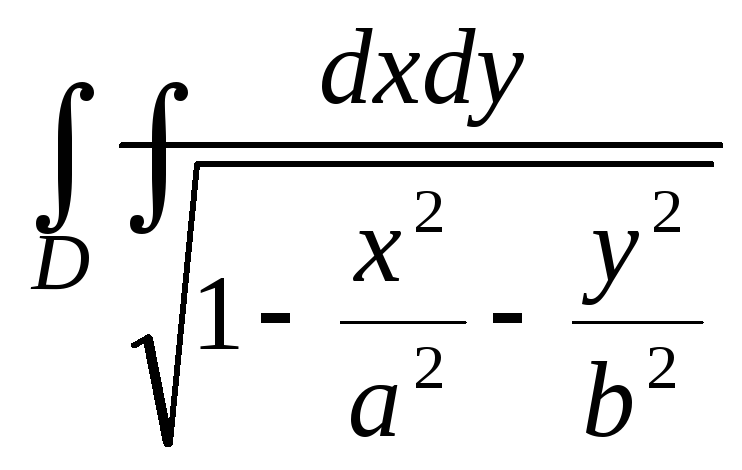 ,
где областьD
определяется неравенством
,
где областьD
определяется неравенством
![]() .
.
Подынтегральная
функция определена во всех точках,
находящихся внутри эллипса
![]() .
На границе области она обращается в
бесконечность. Для выяснения вопроса
сходимости интеграла перейдем к новым
координатам по формулам:
.
На границе области она обращается в
бесконечность. Для выяснения вопроса
сходимости интеграла перейдем к новым
координатам по формулам:![]() ,
,![]() или
или
![]() ,
,
![]() (0
1, 0
2).
(0
1, 0
2).
Получаем
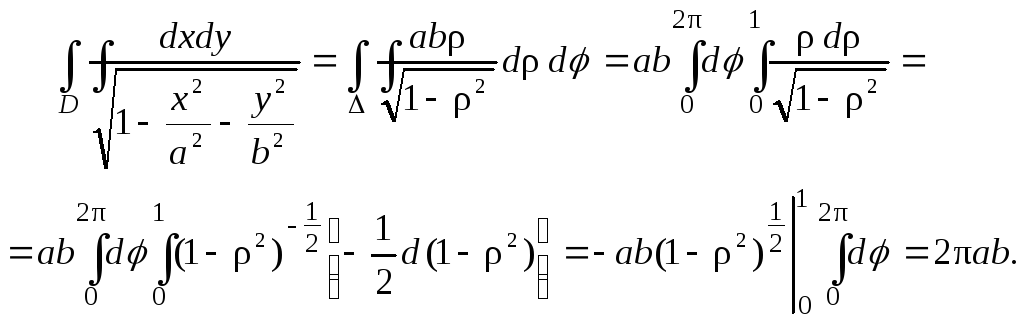
Итак, данный интеграл сходится.
Пример
23. Исследовать,
сходится ли
![]() ,
гдеD
– треугольник, ограниченный прямыми у
= 0, у
= х, х
= .
,
гдеD
– треугольник, ограниченный прямыми у
= 0, у
= х, х
= .
Введем новые переменные по формулам:
![]() ,
,
![]() .
(23)
.
(23)
Преобразование (23) переводит треугольник D плоскости Оху (рис. 37) в треугольник плоскости Ouv, ограниченный прямыми u = v, u + v = 2, v = 0 (рис. 38).
у
v







D
0
х
0
2
u

Рис. 37
Рис. 38
Так
как
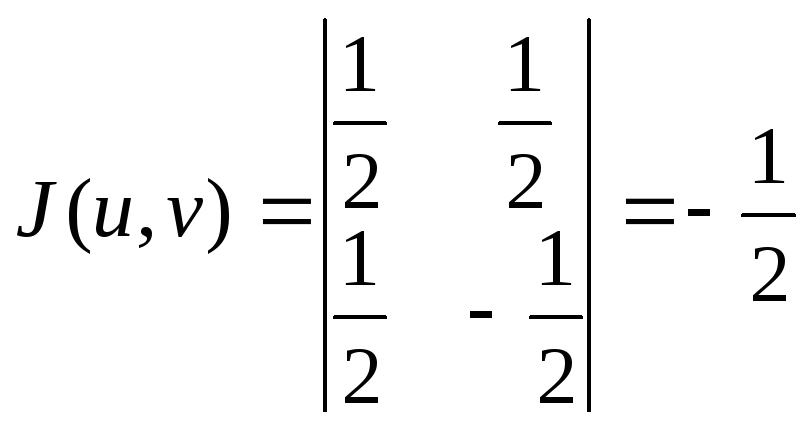 ,
,![]() ,
то
,
то
![]() ,
,
где - треугольник, ограниченный прямыми u = v, u = , v = 0.
Следовательно,
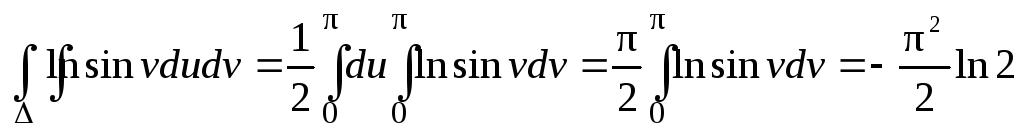 ,
,
т.е. интеграл сходится.
Замечание.
Здесь принято во внимание, что
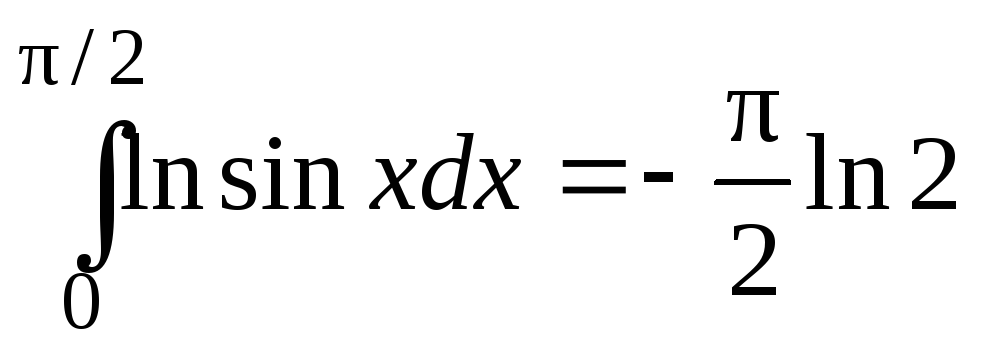 .
.
Этот интеграл (называемый интегралом Эйлера) вычислен с помощью замены переменной. Полагая x = 2t, получаем
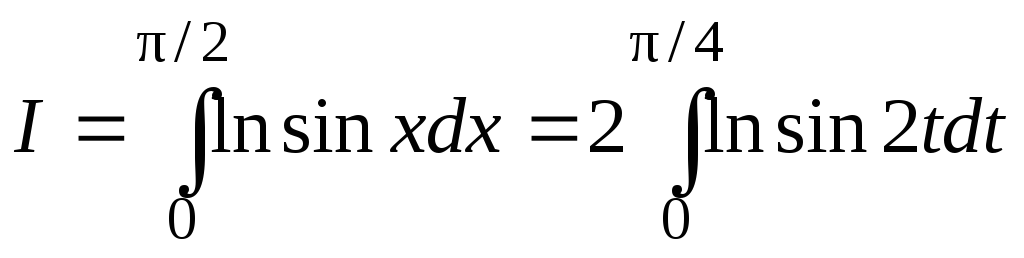 .
.
Так
как
![]() ,
то
,
то
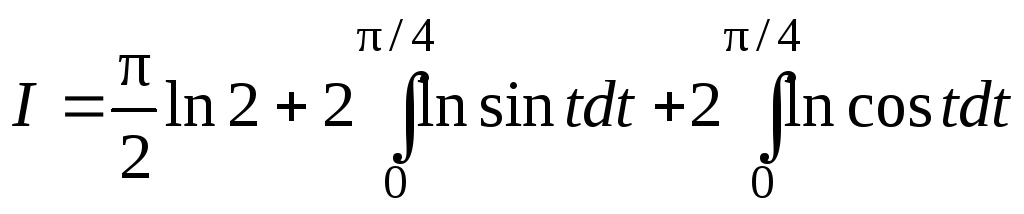 .
.
Последний
интеграл с помощью подстановки
![]() приводится к виду
приводится к виду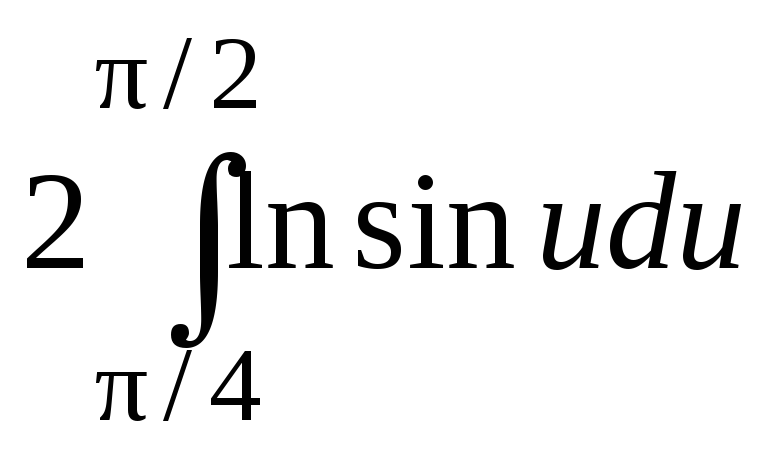 ,
поэтому
,
поэтому
 .
.
Пример
24. Исследовать,
сходится ли
![]() ,
гдеD
определена неравенствами х
0, у
0.
,
гдеD
определена неравенствами х
0, у
0.
Рассмотрим
квадрант круга радиуса R
с центром в начале координат, обозначим
его через KR.
Вводя полярные координаты по формулам
![]() ,
,![]() ,
получаем
,
получаем
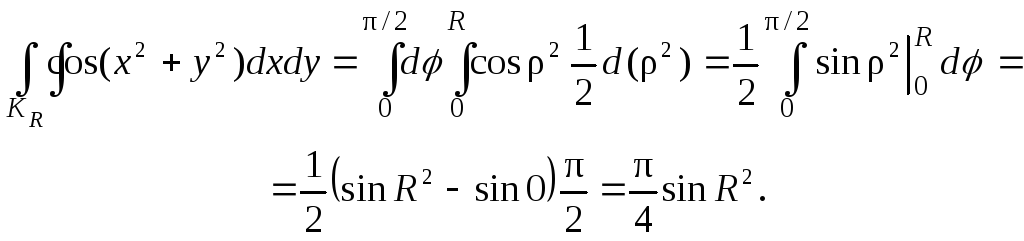
Так как sin R2 при R предела не имеет, данный интеграл расходится.
