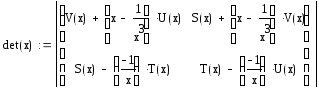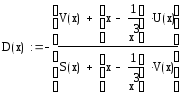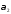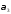4.2 Определние собственных форм колебаний в MathCad

4.3 Определение собственных форм колебаний в Fortran

Программа состоит из двух частей, из непосредственного нахождения собственных форм колебания упругой балки и визуализации результатов.

subroutine MNSU(f,x0,x,m) - Подпрограмма Метода Ньютона для отделения корней уравнения x=x0;m=0.;e=1.;t=1e-5 do while (e>1e-5) fp=(f(x+t)-f(x))/t y=x-f(x)/fp; e=abs(y-x); x=y;m=m+1 end do end Function S(x); S = (cosh(x) + cos(x)) / 2;end -Задаем функции Крылова Function T(x); T=(sinh(x) + sin(x))/2; end Function U(x); U=(cosh(x)-cos(x))/ 2;end Function V(x);V=(sinh(x) - sin(x))/2; end Function det(x); - Задаем саму функцию a11=V(x)+(x-1/x**3)*U(x);a12=S(x)+(x-1/x**3)*V(x); a21=S(x)-(-1/x)*T(x);a22=T(x)-(-1/x)*U(x); det=a11*a22-a12*a21; end program osfk integer,parameter::n=1001; real::d(3), a(3), y(3) external det real(8)::xg(n),yg(n,3) - Описание переменных x0=0.1; xk=8; h=(xk-x0)/(n-1) do i=1,n; x=x0+(i-1)*h; xg(i)=x; yg(i,1)=det(x)/cosh(x); enddo call cls(2) call plotm(10,10,500,300,xg,yg,n,1) -Вызов графической подпрограммы call MNSU(det, 0.96, a(1),m); print*,a(1),m -Уточнение корня call MNSU(det, 4., a(2),m); print*,a(2),m call MNSU(det, 7.2066, a(3),m); print*,a(3),m do j=1,3; d(j)=-(V(a(j))+(a(j)-1/a(j)**3)*U(a(j)))/(S(a(j))+(a(j)-1/a(j)**3)*V(a(j))) enddo -Цикл для вычисления значений D print*,d; h=1./(n-1); yg=0 do i=1,n;z=(i-1)*h y(1)=u(a(1)*z)+d(1)*v(a(1)*z);y(2)=u(a(2)*z)+d(2)*v(a(2)*z);y(3)=u(a(3)*z)+d(3)*v(a(3)*z) !print*,z,char(9),y(1),char(9),y(2),char(9),y(3);xg(i)=z; yg(i,:)=y -Функция форм колебаний enddo do j=1,3; yg(:,j)=yg(:,j)/maxval(abs(yg(:,j))); enddo call plotm(10,310,500,610,xg,yg,n,3) -Рисуем формы колебаний end

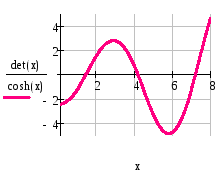
Результаты представлены на рис. 4.2. и в таблице 4.2.

Корни уравнения (4.3), полученные в Fortran. Таблица 4.2

1.464186	4.162954	7.206529

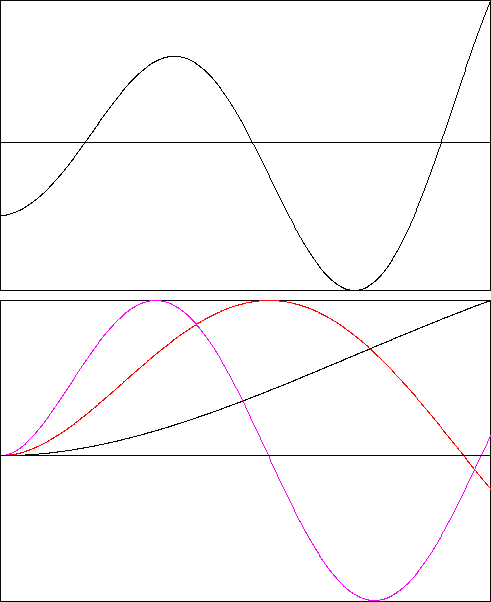
Рис. 4.2 График функции (4.3) и три формы колебания балки

4.4 Определение собственных форм колебений в Excel

Обозначим x0 как x начальное, а xk как x конечное. Задаем количество точек равное 31. Вычисляем шаг по известной нам формуле. Затем вычисляем значения S(x), U(x), T(x), V(x) по формулам (4.1). Далее считаем коэффициенты матрицы по формуле (4.3) и находим определитель. Строим график зависимости значений x от значений определителя (рис 4.3).

Рис. 4.3

4.5 Вывод

Корни уравнения и три формы колебаний, полученные разными программными продуктами, совпали. Задача решена правильно.

5 ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ВЕЛИЧИН

5.1 Постановка задачи

Для области D в плоскости Z нужно построить конформно отображённую функцией

W= f(Z) область D* в плоскости W. Для этого нужно:

1. записать уравнения, описывающие границы области D;

2. выбрать (вычислить) на границах области D не менее 20 точек Zк таким

образом, чтобы при их обходе область оставалась всегда слева;

3. вычислить точки Wк = f(Zк) области D*;

4. по найденным точкам построить области D и D*. D: ;W:

5.2 Получение конформного отображения с помошью Fortran

Для начала указываем комплексные велечины w и z, после чего задаём шаг h и цикл. Для нахождения z=x+iy нужно найти х и у по формуле Эйлера

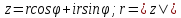(5.1)

Затем находим 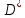, решив заданную формулуW и сделав х1 –реальной частью W, а у1 – мнимой. После вывода результатов х,у,х1,у1 строим график в excel.

complex z,w h=6.28/30. do i=0,30 f=i*h; x=3*cos(f); y=3.*sin(f) z=cmplx(x,y); w=(z+1/z)/2 x1=real(w); y1=imag(w) print*,x,char(9),y,char(9),x1,char(9),y1 enddo end

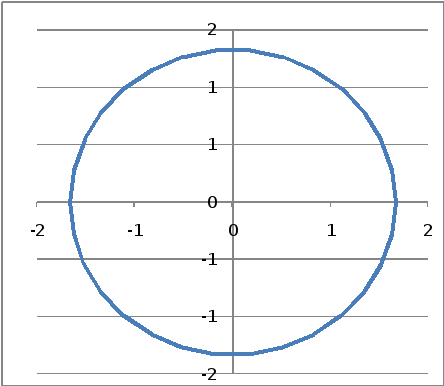
Рис. 5.1 Область D

Рис. 5.2 Область