
Методические указания. Понятов
.pdf
2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2.1. Основные понятия
Производной y функции y f (x) по аргументу х называется предел отношения приращения функции y f (x x) f (x) к вызвавшему его приращению аргумента x , при стремлении приращения аргумента к нулю:
|
lim |
f (x x) f (x) |
lim |
y |
y |
x |
x |
||
|
x 0 |
x 0 |
Если существует конечный предел, то функция y f (x) называется дифференцируемой в точке х (имеющей производную).Операция нахождения производ-
ной называется дифференцированием функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, или |
|
|
|
dy |
, или |
df (x) |
d |
f (x) |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Производная обозначается y |
|
f (x) , или |
dx |
dx |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Пример 15. Найти производную функции y sin x по определению. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Решение. |
y lim |
y |
lim sin(x x) sin x lim |
2cos(x x / 2)sin( x / 2) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 0 |
x |
|
|
x 0 |
|
x |
|
|
|
x 0 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim cos(x x / 2) lim sin( x / 2) cos x 1 cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
x / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
На практике используют таблицу производных основных элементар- |
|||||||||||||||||||||||||||||||||||||||||||||||
ных функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.1. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
I |
|
xn |
nxn 1 |
|
|
VI |
|
|
ln x |
x |
XI |
|
ctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
II |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
VII |
|
loga x |
|
|
|
|
|
XII |
arcsinx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 x |
|
|
|
|
xln x |
|
1 x2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
III |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VIII |
|
sin x |
cosx |
XIII |
|
|
1 x |
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
IV |
|
|
ex ex |
|
|
|
|
|
|
IX |
|
cosx |
sin x |
XIV |
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
V |
|
ax ax ln a |
|
|
X |
|
tgx |
|
|
XV |
arcctgx |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
cos2 x |
|
|
1 x2 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
Геометрически производная f (x0 ) равна угловому коэффициенту каса-
тельной к графику функции f(x) в точке (x0, f(x0)), т.е. f (x0 ) tg , где - угол наклона касательной. Уравнение касательной имеет вид y y0 f (x0 )(x x0 )
Физический смысл производной функции f(t), где t– время, а f(t)– закон движения (изменения координат) – мгновенная скорость движения. Обобщая, можно сказать, что производная – есть скорость изменения функции в точке х.
Производной второго порядка(второй производной) называют произ-
водную от производной |
y d 2 y |
(y ) . Аналогично рекуррентно определяют |
|||||||||
|
|
dx2 |
|
|
|
|
n 1 |
|
|
|
|
все производные высших порядков y |
(n) |
(y |
|
|
|||||||
|
|
) . |
|
|
|||||||
Дифференциалом (первого порядка) функции называют произведение |
|||||||||||
|
|
|
|
|
|
|
|
|
|
dx x . |
|
производной на дифференциал аргумента dy y dx, принято |
|||||||||||
Дифференциальное исчисление– есть изучение производных и дифферен- |
|||||||||||
циалов функций и их применение к исследованию функций. |
|
|
|||||||||
2.2. Основные правила дифференцирования. |
|
|
|
||||||||
Пусть u=u(x), v=v(x)– функции, имеющие производную, c–постоянная. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1) c 0 ; |
2) x 1; |
3) (u v) |
u |
v ; |
4) (u v) |
u |
v u v ; |
||||
|
|
u |
|
|
|
|
|
|
|
|
|
u v v u |
, если v 0. |
|
|
||||||||
5) (c u) |
c u ; |
6) |
|
|
v2 |
|
|
|
|
||
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
Пример16. (3e |
x |
|
|
|
|
|
x |
|
|
|
|
3e |
x |
1 0 3e |
x |
1; |
|
|
|
|
||||
|
|
|
|
x 9) 3 |
(e ) |
x |
9 |
|
|
|
|
|
|
|
|||||||||||||
(7 |
x |
|
|
(7 |
x |
sin x 7 |
x |
|
|
7 |
x |
ln 7 |
sin x 7 |
x |
cosx ; |
|
|
|
|
|
|
||||||
|
sin x) |
) |
|
(sin x) |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos cosx sin x ( sin x) |
|
1 |
|
|
|||||||
|
|
sin x |
|
(sin x) |
cosx sin x (cosx) |
|
|
|
|
||||||||||||||||||
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
cos2 x |
|
|
cos2 |
|
|||||||||
|
|
|
cosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||
7)Производная сложной функции. Пусть y= f(u),u = u(x), то y y u
xu x
Если функция y = f(u) элементарная, то в соответствии с таблицей произ-
|
|
|
|
|
|
|
|
|
(eu ) eu u , и т.д. |
||
водных 2.1 получим un nun 1 u , (sinu) cos u u , |
|||||||||||
Пример17. Найти производную функции y ln x3 2x 5 . |
|||||||||||
Решение: обозначим u x3 |
2x 5 , тогда, |
y ln u и по правилу 7 получаем |
|||||||||
|
|
1 |
|
1 |
|
3 |
|
|
3x2 2 |
||
y |
ln u |
u u |
|
|
|
x |
2x 5 |
|
|
. |
|
x3 2x 5 |
x3 2x 5 |
||||||||||
На практике обычно замену наu, приводящую функцию к элементарному виду, делают в уме, и записывают результат сразу для х.
12

8) Логарифмическое дифференцирование. Заключается в том, что сна-
чала находят производную от логарифма функции (ln f (x)) , а затем производ-
|
|
|
|
ную самой функции по формуле f (x) (ln f (x)) f (x) , поскольку в соответст- |
|||
|
|
|
|
|
f (x) |
|
|
вии с правилом 7, можно записать ln f (x) |
|
|
. Обычно его применяют |
f (x) |
|||
для функций вида y uv (функция в основании и показателе степени).
Пример18. Найти производную функции y xsin x .
Решение. Находим производную от логарифма функции ln y sin x ln x
|
|
1 |
|
|
|
y |
|
cosx ln x |
sin x |
x |
sin x |
|
cosx ln x sin x |
|
, тогда |
y |
(ln y) |
|
|
|
. |
||||
(ln y) |
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
|
|
9) Дифференцирование неявной функции. В общем виде неявную функцию можно записать в виде F(x,y) = 0. Продифференцировав по х обе части этого уравнения получим уравнение для y , откуда и найдем y .
Пример 19. Найти производную y из уравнения y2 x3 xsin y 8 0 . Решение. Дифференцируем обе части уравнения, считая y сложной функцией:
2yy 3x |
2 |
sin y xcos y y |
|
|
|
|
3x2 |
sin y |
|
|
|
||||||
|
|
|
|
|
|
. |
|
||||||||||
|
0 , откуда y |
2y xcos y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10) Дифференцирование функции, заданной параметрически. |
|||||||||||||||||
Еслиx = x(t), y = y(t), то yx |
yt |
или dy |
dy dt . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
xt |
|
dx |
dx dt |
|
|
|
|
|
|
|
|
|
Пример20. Найти производную |
y , если y 2t4 |
3t 5 |
и x t3 |
7t2 . |
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3t |
2 |
14t . Следовательно, |
|
|
8t3 3 |
|
||||||
|
|
|
|
y |
3t |
|
14t . |
||||||||||
Решение. Находим yt 8t |
|
3, xt |
|
x |
|
2 |
|||||||||||
2.3. Правило Лопиталя раскрытия неопределенностей {0/0} и{ / }
Пусть функции f(x) иg(x) дифференцируемы в окрестности точки х0, и
g (x) 0. Если lim |
f (x) lim g(x) 0или lim |
f (x) lim g(x) , то |
|||
x x0 |
x x0 |
|
x x0 |
|
x x0 |
|
|
f (x) |
|
|
|
|
lim |
lim |
f (x) |
, |
|
|
g(x) |
g (x) |
|||
|
x x0 |
x x0 |
|
||
|
|
|
|
||
если предел в правой части равенства существует.
13
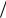
|
|
f |
|
0 |
|
|
|
lim |
(x) |
||||
Если |
|
|
снова дает неопределенность |
и |
||
g (x) |
||||||
|
x x0 |
0 |
|
|||
|
|
|
|
|
||
|
|
|
, и f (x) и g (x) |
удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д. Перед взятием вторых производных и т.д. надо произвести все возможные упрощения выражения.
Неопределенности 0 и путем преобразований могут быть сведены к неопределенностям 0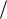 0 или
0 или 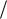 , что позволит воспользоваться правилом Лопиталя. В случае неопределенностей 00 , 1 и 0 следует найти предел логарифма функции.
, что позволит воспользоваться правилом Лопиталя. В случае неопределенностей 00 , 1 и 0 следует найти предел логарифма функции.
|
|
sin x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
cosx |
|
cos0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример21. lim |
|
lim |
sin x |
|
|
lim |
|
1; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x 0 |
|
|
x |
|
|
|
0 |
|
x 0 |
|
|
|
|
|
|
|
|
|
x 0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||
Пример 22. lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
lim |
|
|
0 . |
|||||||||||||||||
|
|
|
2x |
|
|
|
|
|
|
|
2x |
|
e2x |
|
|
2x |
|||||||||||||||||||||||||||||||
|
x |
e |
|
|
|
|
|
x |
|
|
|
|
|
|
x |
2e |
|
|
|
|
|
x |
|
x |
2e |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример23.Найти предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 x |
|
|
|
|
ex 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Сведем неопределенность к |
0 0 , приведя дроби к общему |
||||||||||||||||||||||||||||||||||||||||||||||
знаменателю. Затем применим дважды правило Лопиталя. |
ex |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex 1 x |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
|
1 x |
|
|
|
|
||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x 0 |
x |
|
|
|
e 1 |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
x e 1 |
0 |
|
x 0 |
|
xex |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ex |
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
1 |
; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
|
x |
|
|
|
|
|||||||||||||||||
x 0 |
e |
|
xe |
|
1 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
e e xe 2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ex xex 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2.4. Исследование функции Порядок полного исследования функции.
I.Общая характеристика функции
1)Нахождение области определения функции (ООФ).
2)Нахождение точек пересечения графика с осями Ох (у = 0) и Оу (х= 0) и интервалов знакопостоянства.
3)Выяснение вопроса о четности, нечетности, периодичности функции.
4)Нахождение и классификация точек разрыва функции.
5)Нахождение асимптот функции
II.Исследование функции с помощью первой производной:
6)Определение интервалов возрастания и убывания функции.
7)Нахождение точек экстремума.
III.Исследование функции с помощью второй производной:
8)Определение интервалов выпуклости и вогнутости графика функции.
14
9) Нахождение точек перегиба. IV. Построение графика функции.
Функция f (x) называется четной, если f ( x) f (x) , график такой функции симметричен относительно оси ординат (Оу). Функция f (x) называется нечетной, если f ( x) f (x) , график такой функции центральносимметричен относительно начала координат. Остальные функции называются функциями общего вида. Они тоже могут иметь симметрию, но другого вида.
Функция f (x) называется периодической с периодом Т 0, если f (x Т) f (x) . Практически периодом называют наименьшее из положительных чисел Т, тогда любой другой период имеет вид nT, где n = 1,2,…Значения и график периодической функции повторяются через Т, следовательно, такую функцию достаточно исследовать на одном периоде. Из элементарных функций периодическими являются только чистотригонометрические. Остальные функции являются непериодическими.
Исследование на непрерывность.
Функция f (x) называется непрерывной в точке x0 , если она определена в
некоторой окрестности точки x0 и существует предел lim f (x) f (x0 ) или
x x0
lim |
f (x) lim f (x) f (x0 ) . |
(1) |
x x0 0 |
x x0 0 |
|
Если функция непрерывна в каждой точке некоторой области, то она на- |
||
зывается непрерывной в этой области. |
|
|
Точка x0 называется точкой разрыва функции |
f (x) , если функция оп- |
|
ределена в некоторой окрестности точки x0 , и для нее нарушается условие не-
прерывности (1). Точка разрыва называется точкой разрыва I рода, если односторонние пределы в (1) существуют и конечны. Если они при этом равны между собой, но не равны f (x0 ) , то x0 точка устранимого разрыва, если различ-
ны, то точка неустранимого разрыва. В последнем случае разность правого и левого пределов называется скачком функции. Точка разрыва называется точкой разрыва II рода, если хотя бы один из односторонних пределов в (1) равен бесконечности или не существует.
Теорема. Все элементарные функции непрерывны в своей ООФ. Сумма и произведение непрерывных функций есть также функция непрерывная. Частное от деления двух непрерывных функция – есть функция непрерывная во всех точках, где нет деления на нуль.
Это означает, что у элементарной функции разрывы могут быть только в точках, где функция не существует, в граничных точках ООФ. Например, в точках деления на нуль. Для составных функций подозрительными на разрыв являются точки стыковки элементарных частей.
15
Если расстояние между точкой кривой и некоторой прямой стремится к
нулю |
при удалении от начала координат, то эта |
прямая называется |
а |
кривой. |
|
|
1. Прямая х = а является вертикальной асимптотой, если функция неог- |
|
раниченно возрастает при х а, т.е. lim f (x) и/или |
lim f (x) . Точка а |
|
|
x a 0 |
x a 0 |
является точкой разрыва II рода.
2. Прямая у = b является горизонтальной асимптотой, если существует
конечный и равный b предел функции f (x) |
при х , т.е. если |
lim f (x) b |
|||
|
|
|
|
|
x |
и/или |
lim f (x) b . |
|
|
||
x |
|
|
|
||
3. Уравнение наклонной асимптоты |
имеет вид y = |
kx +b, где |
|||
k lim |
f (x) |
, |
b lim f (x) kx (при необходимости надо отдельно рассматривать |
||
|
|||||
x |
x |
x |
|
|
|
х + и х – ). Наклонная асимптота существует, если пределы для k иb конечны. При k= 0 и конечном значенииb асимптота получается горизонтальной. Поэтому на практике поиск горизонтальной асимптоты отдельно можно не проводить, сразу начиная с наклонной асимптоты (нахождения k).
Функция f (x) называется возрастающей, если из неравенства x2 x1 следует неравенство f (x2 ) f (x1) . Если же из неравенства x2 x1 следует неравенство f (x2 ) f (x1) , то функция f (x) называется убывающей.
Если во всех точках некоторого интервала f (x) 0 , то функция f (x) возрастает, если f (x) 0 , то f (x) убывает в этом интервале
Функция f (x) имеет экстремум (максимум или минимум) в точке x0 , если значение функции в этой точке f (x0 ) является наибольшим или наименьшим
значением функции в некоторой окрестности этой точки.
Следует помнить: 1) Максимум (минимум) не является обязательно наибольшим (наименьшим) значением, принимаемым функцией. Вне рассматриваемой окрестности точки x0 функция может принимать большие (меньшие)
значения, чем в этой точке. 2) Функция может иметь несколько максимумов и минимумов.
Необходимое условие экстремума. Если функция f (x) имеет экстремум в точке x0 , то её производная в этой точке равна нулю f (x0 ) 0 (дифферен-
цируемая функция)или не существует.
Это означает, что точки экстремума следует искать только среди точек, где f (x0 ) 0 или производная не существует, их называют критическими точками первого рода(точки с f (x0 ) 0 называют стационарными). Другие
точки исследовать не нужно. Следует понимать, что это условие не достаточное, поскольку производная может быть равна нулю f (x) 0 или не существо-
16

вать не только в точках экстремумов. Поэтому после нахождения критических точек каждую из них надо исследовать на основании достаточных условий.
Первое достаточное условие существования экстремума (по первой производной).Пусть точка x0 является критической точкой функции f (x) . Ес-
ли при переходе слева направо через x0 : 1) f (x) меняет свой знак с + на–, то точка x0 - точка максимума; 2) f (x) меняет свой знак с – на +, то точка x0 - точка минимума; 3) f (x) не меняет знака, то экстремума нет.
В качестве примера функции, у которой в точке экстремума производная не существует, приведем y x . В точке х = 0 эта функция производной не
имеет (не дифференцируема), но по первому условию - это точка минимума.
Второе достаточное условие существования экстремума (по второй производной). Пусть в точке x0 f (x0 ) 0 . Тогда x0 – точка максимума, если f (x) 0 , и минимума, если f (x) 0 . Если же f (x) 0 , то для заключения о наличии экстремума требуется дополнительное исследование (например, по первому условию).
График функции f (x) называется выпуклым в интервале (а, b), если он расположен ниже касательной, проведенной в любой точке интервала, и вогну-
тым, если выше. Достаточным условием выпуклости (вогнутости) является f (x) 0 ( f (x) 0 ) в (а, b).
Точки, где f (x) 0 или f (x) не существует, называют критическими точками второго рода. Если при переходе слева направо через такую точку f (x) меняет свой знак, то эта точка является точкой перегиба, т.е. по одну сторону от нее кривая выпукла, по другую – вогнута.
Пример 24.Исследовать функцию y |
x4 |
|
; |
||
x3 |
1 |
||||
Решение. I. ООФ D(y) ,1 1, ; |
|
||||
|
|
|
|
||
Пересечение с осями у=0 при х=0. Интервалы знакопостоянства покажем на оси, отметив на ней точки пересечения с осями и разрыва функции.
|
|
|
|
|
– |
|
|
|
– |
|
+ |
f(x) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
(-, 0) |
|
|
0 |
(0, 1) |
1 |
(0, +) |
x |
|||
y( x) |
x 4 |
|
|
|
x4 |
|
y(x) и y(x) , следовательно, общего вида. Функция |
||||||
x 3 |
1 |
|
x3 |
1 |
|||||||||
|
|
|
|
|
|
|
|
||||||
непериодична, поскольку является элементарной нетригонометрической. Функция является элементарной, следовательно, она непрерывна везде,
кроме точки х = 1, где не существует. Определяем тип точки разрыва.
17

|
lim |
x4 |
|
lim |
1 |
|
|
, |
|
lim |
|
x4 |
|
|
lim |
1 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||
|
x 1 0 x3 1 |
|
x 1 0 x3 1 |
|
|
|
|
|
x 1 0 x3 1 |
|
x 1 0 x3 |
|
|
|
|
|
|
|||||||||||||||||||||||||
точка х = 1 – точка разрыва второго рода; прямая х = 1 – |
вертикальная асим- |
|||||||||||||||||||||||||||||||||||||||||
птота. Ищем наклонные асимптоты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
k lim |
f (x) |
lim |
|
|
|
x4 |
lim |
|
x3 |
lim |
|
|
1 |
|
|
|
1 |
, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 1/ x3 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
x |
x |
|
|
|
|
x x x3 1 |
|
x x3 1 |
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b lim f (x) kx lim |
|
x4 |
|
x |
lim |
x4 |
x4 x |
lim |
|
|
|
x |
|
|
lim |
|
|
1 |
0 |
. |
||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
x |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
|
x x |
|
|
|
|
|
x |
|
|
|
x x |
|
1 |
|
x x |
|
1/ x |
|
|||||||||||||||||||||||
Таким образом, прямаяy = kx +b = х, двусторонняя наклонная асимптота.
II. Исследование функции с помощью первой производной:
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
4 |
||
|
|
|
4 |
|
|
3 |
3 |
4 |
|
2 |
|
6 |
4x |
3 |
|
3 |
3 |
||||||
|
|
|
x |
|
|
|
4x |
|
1 x |
3x |
|
x |
|
|
|
x |
|
||||||
|
3 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
1 |
|
|
x3 1 |
|
|
x3 1 |
|
|
x3 1 |
|||||||||||
Находим критические точки первого рода:
—стационарные точки y = 0 или x3 x3 4 0 . x1 0, x2 3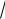 4 1,59
4 1,59
—производная не существует в точке х = 1.
Определяем интервалы монотонности (возрастания и убывания) функции и точки экстремума. Результаты сведем в таблицу.
|
|
|
(- , 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0, + ) |
||||||
|
x |
|
|
|
|
0 |
|
(0,1) |
|
|
1 |
|
|
|
(1, 3 4 ) |
|
|
3 4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
+ |
|
|
|
|
0 |
|
– |
|
Не сущ. |
– |
|
|
0 |
|
|
|
|
|
+ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
Max |
|
|
|
Не сущ. |
|
|
|
|
Min |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y = 0 |
|
|
|
|
|
|
y 43 |
4 3 2,18 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
III. Исследование функции с помощью второй производной: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x6 4x3 |
|
|
|
|
6x5 |
12x2 x3 |
1 2 x6 4x3 2 3x2 x3 1 |
|
|
|
|
|
x3 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
6x2 |
|||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
3 |
1 |
|
|
|
|
|
x |
3 |
1 |
|
|
|
|
|
x |
3 |
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||
Находим критические точки второго рода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
— y = 0 или x2 |
x3 2 0 . x 0, x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
1,26 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
— вторая производная не существует в точке х = 1.
Определяем интервалы выпуклости и вогнутости функции точек перегиба Результаты сведем в таблицу.
18
|
x |
(- , 3 |
2 ) |
|
|
3 |
|
|
|
( 3 |
2 |
,0) |
0 |
|
(0, 1) |
|
1 |
|
(1, + ) |
|||
|
2 |
|
|
|||||||||||||||||||
|
y |
+ |
|
|
0 |
|
|
|
|
– |
0 |
|
– |
|
Не сущ. |
|
+ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
т. пере- |
|
|
|
|
|
Нет пе- |
|
|
Нет пе- |
|
|
||||
|
y |
|
|
|
|
|
гиба |
|
|
|
|
|
региба |
|
|
региба |
|
|
||||
|
|
|
|
|
|
y = -0,84 |
|
|
|
|
|
y = 0 |
|
|
Не сущ. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
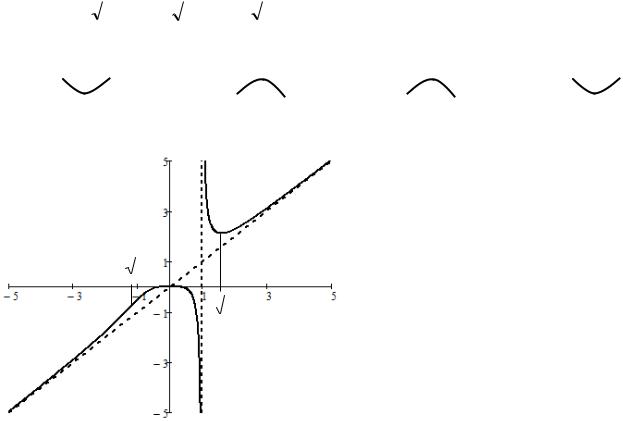
График функции приведен на ри- |
|||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сунке слева. Пунктиром показаны |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
асимптоты. При его построении |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следует соблюдать |
несколько |
||||
|
|
|
|
|
|
|
|
|
|
|
|
y = x |
|
|
правил. Масштаб по осям надо |
|||||||
|
|
|
3 |
2 |
|
|
|
|
|
|
|
выбрать так, чтобы максимальные |
||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
характерные значения х и у (экс- |
||||||||||
|
|
|
|
|
4 |
|
|
x |
|
тремумы, точки перегиба и т.д.) |
||||||||||||
|
|
|
|
|
|
|
|
|
x = 1 |
|
|
располагались от начала отсчета |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
не далее, чем середина полуоси. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построение |
следует начинать с |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
асимптот и характерных значе- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ний. График |
|
строится |
|
поэтапно |
|
для каждого интервала между характерными значениями, правильно строя поведение функции в этих точках.
Наибольшее и наименьшее значение функции на отрезке
Если функция непрерывна на отрезке [a, b], то на этом отрезке всегда имеются точки, в которых она принимает наибольшее и наименьшее значения. Этих значений функция достигает либо в точках экстремума, принадлежащих отрезку, либо на концах отрезка. В соответствии с этим, для нахождения наибольшего и наименьшего значения функции на отрезке надо:
1)Определить критические (стационарные) точки функции, принадлежащие отрезку (заметим, что исследовать на экстремум не нужно, поскольку потом нужные точки будут отобраны по значению).
2)Вычислить значения функции в этих критических точках и на концах отрезка [a, b] (т.е. при х = а или х = b).
3)Наибольшее и наименьшее из найденных значений и будут соответственно наибольшим и наименьшим значением функции на отрезке.
|
Пример |
25.Найти наибольшее и наименьшее значение функции |
||||||
y |
x4 |
|
2 3 |
|
3 |
2 |
2 |
на отрезке [–4/3,2]. |
|
3 x |
2 x |
|
|||||
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
Решение. 1) Находим критические (стационарные) точки функции y 0:
19

|
x |
3 |
2x |
2 |
3x x x |
2 |
2x 3 0 , откуда x1 0; |
2 |
2x 3 0, x2 |
1, x3 |
3 . |
|
y |
|
|
|
x |
||||||||
Критические точки x1 0 и |
x2 1 принадлежат отрезку [-4/3, 2], |
а x3 3 |
– не |
|||||||||
принадлежит. 2) Вычисляем значения функции для х1 и х2 и на концах отрезка. y(0) = 2, у(–1) = 17/12 1,42, у(–4/3) =46/27 1,42, у(2) = –16/3 -5,33.
3) Наименьшим из найденных значений является –16/3, а наибольшим 2. Это означает, что наибольшего значения 2 функция достигает в критической точке х = 0, а наименьшего –16/3 – на правом краю отрезка х = 2.
2.5. Функции нескольких переменных
Частной производной от функции z = f(x, y) по независимой переменной х
|
|
f (x x, y) f (x, y) |
|
z |
|
|
|
называется конечный предел |
lim |
|
|
|
zx fx (x, y) , вычис- |
||
x |
x |
||||||
|
x 0 |
|
|
|
|||
ленный при постоянном у. Частной производной по у называется конечный
|
|
f (x, y y) f (x, y) |
|
z |
|
|
|
|
предел |
lim |
|
|
|
zy fy |
(x, y) , вычисленный при постоян- |
||
y |
y |
|||||||
|
y 0 |
|
|
|
|
|||
ном х. Аналогично определяются частные производные от функции большего числа независимых переменных.
Вычисление частных производных производится по тем же правилам, что и производных функции одной переменной при соблюдении правила:
При взятии производной по одной независимой переменной все остальные считаются постоянными (константами).
Полный дифференциал функции z = f(x, y) вычисляется по формуле dz xz dx yz dy .
Частные производные второго порядка, также как и ранее, есть производные от производной. Но, поскольку второе дифференцирование для функции z=f(x, y)проводится от двух частных производных по двум переменным, это приводит к появлению четырех частных производных второго порядка:
|
z |
|
|
2 z |
z , |
|
z |
|
|
2 z |
z |
|
|
z |
|
|
2 z |
z , |
|
z |
|
|
2 z |
z . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
x y |
|
y |
|
|
y x |
||||||||||||||||||
|
x x |
|
|
2 |
xx |
|
x y |
|
|
xy |
|
|
y y |
|
|
2 |
yy |
|
y x |
|
|
yx |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично определяются частные производные высших порядков. |
|
||||||||||||||||||||||||||
|
Производные |
|
|
|
|
|
в которых дифференцирование происходит по |
||||||||||||||||||||
|
zxy и |
|
zyx , |
||||||||||||||||||||||||
обеим переменным в разном порядке, называются смешанными. Справедлива теорема: если частные производные непрерывны, то они не зависят от порядка
|
|
|
|
|
и т.д. |
дифференцирования, т.е. zxy zyx, |
zxyy zyxy zyyx |
||||
Дифференцирование сложных функций z = f(u,v),гдеu=u(x,y), v=v(x,y):
20
