Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Университет им. Н.И. Лобачевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛЕКЦИИ_ПО_ВЫСШЕЙ_МАТЕМ_Голубев

.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

4.74 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2625 26 > Следующая >>>

Область сходимости.

Теорема. Если степенной ряд

а хn

сходится при х=х0, то он сходится для любого х,

n 1

удовлетворяющего неравенству |x|<|x0|, причем абсолютно.

Доказательство.

аn х0n

аn х0n =0, а следовательно | аn х0n |

ограничена, т.е. |аn х0n |M0.

1. Так как ряд

сходится, то

lim

n 1

хn |

2. Если х0 0, то очевидно |а

xn|=|а

. Заметим, что при |x|<|x0|

ряд

n 1

сходится, что влечет за собой сходимость ряда

|а хn| в той же области D{|x|<|x0|}.

n 1

Таким образом ряд

а хn сходится абсолютно при всех х,

n 1

удовлетворяющих неравенству |x|<|x0|.

Следствие. Если ряд

а хn расходится при х=х0, то он также расходится при всяком х, для которого

n 1

имеет место неравенство |x|>|x0|.

Радиус сходимости.

Определение. Величина Rсх 0

(число или символ + ) называется радиусом сходимости ряда

a xn,

n 1

если при всех х удовлетворяющих |x|<Rсх

данный ряд сходится, а для всех х удовлетворяющих |x|>Rсх

расходится.

Определение.

Множество х(-Rсх, Rсх) называется кругом сходимости ряда

a xn.

n 1

Теорема.

Всякий степенной ряд

a xn имеет область сходимости.

n 1

Доказательство. Точка х=0 всегда принадлежит области сходимости ряда anxn. Если при всех х0 n 1

ряд расходится, то радиус сходимости Rсх=0.

1. Если ряд сходится при х=х0 и расходится при |x|>|x0|, то область сходимости будет множество (-х0, х0) и радиус сходимости этого ряда равен |x0| (Rсх=|x0|).

2. Если ряд сходится при любом вещественном х, то область сходимости ряда anxn совпадает с

n 1

множеством вещественных чисел и радиус сходимости этого ряда равен + (Rcx=+ ).

Замечание.

Радиус сходимости ряда

anxn находится по формулам:

n 1

или R =

lim

a n

, которые являются следствием признаков Коши и Даламбера

lim n |a n |

a n 1

соответственно.

Примеры.

n! xn.

n 1

Rcx= lim =0 . Область сходимости D={x| x=0}

n (n 1)!

n 1

=+ , так как

lim n

=0. D R.

lim

xn.

n 1

Rcx=

=1. D={x| x (-1; 1)}.

lim

n 1

lim

(n 1)2

=1. D={x| x (-1; 1)}.

n n

n 1

Rcx=

=+ . D R.

lim

6. 3n-1xn.

n 1

Rcx=

=1/3. D={x| x (-1/3; 1/3}.

3n 1

lim

( 2)n

(x+1)n

n 1

Rcx=

=1/3. Заметим, что область абсолютной сходимости этого ряда будет интервал (-

( 2)n

lim n

4/3;

-2/3)

3. Свойства степенных рядов.

Определение. Ряд

un(x)

называется равномерно сходящимся в области D, если в этой области

n 1

последовательность его частичных сумм Sn(x)= uk(x) равномерно сходится к своей предельной функции

k 1

f(x), то есть: для любого числа >0 можно найти число n0 N такая, что при всех n>n0 и любого

p N имеет

неравенство |Sn+p(x)-Sn(x)|< при всех х из D.

Теорема. В любой замкнутой области, лежащей внутри области сходимости степенного ряда, сумма ряда

f(x) является непрерывной функцией.

Теорема. (признак Вейерштрасса равномерной сходимости)

Если для ряда

un(x)

имеет место неравенство |un(x)| cn при всех х из D и числовой ряд

сn

n 1

сходится, то ряд

un(x) сходится в D равномерно.

n 1

Замечание. Степенной ряд

аnxn всегда равномерно сходится в области -Rcx, Rcx), т.к. для него

n 1

имеет место неравенство |anxn|<anR0n,

где R0<Rcx.

Теорема. Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то

a nxndx

a nxndx =

n 1 a

n 1

Замечание. Последнее утверждение можно сформулировать следующим образом: если пределы интегрирования лежит внутри интервала сходимости степенного ряда, то степенной ряд можно почленно интегрировать.

Примеры.

Имеем :

(-1)nxn=1-x+x2-x3+...+(-1)nxn+...=

. Указанный ряд сходится при |x| r0<R , R

=1.

n 0

1 x

Тогда имеет место равенства при |x|<1:

n 1

(-1)nxndx=

(-1)n

или

ln |x+1|=

(-1)n

1 x

n 1

n 0 0

n 0

Имеем

(-1)n-1x2(n-1)

1 x2

n 1

Этот ряд равномерно сходится при |x|<1. Значит при указанных х имеет место:

2n 1

(-1)n-1x2(n-1)dx или arctg x=

(-1)n-1

1 x2

2n 1

n 1 0

n 1

Теорема. Степенной ряд anxn внутри промежутка сходимости можно дифференцировать, т.е. имеет

n 1

место равенство:

( a xn) =

(a xn) .

n 1

Пример.

Так как

xn=

, R =1; D {x| x (-1; 1)}.

n 1

1 х

Тогда,

(xn) =1+2x+3x2+...+nxn-1+...=

n 1

=1+2х+3х2+...+nxn-1+...=

nxn-1.

(1 х)2

n 1

nxn-1, то есть

n 1

Дифференцирование в области х(-1; 1)					можно продолжить.
		1

				=2+6х+12х2+...+n(n-1)xn-2+...=		n(n-1)xn-2 или


		(1 х)2			n 2
		(1 х)2			n 2
		1 2
			=6+24х+...+n(n-1)(n-2)xn-3+...=			n(n-1)(n-2)xn-3.
	(1 х)3		=6+24х+...+n(n-1)(n-2)xn-3+...=			n(n-1)(n-2)xn-3.
	(1 х)3				n 2
Лекция 31					ФОРМУЛА И РЯД ТЕЙЛОРА

				1. Формула Тейлора.
		В этой лекции мы получим одну из важнейших формул математического анализа, которая имеет большое
прикладное значение - формулу Тейлора.
		Идея формулы заключается в следующем:
Для функции f(x), имеющей все производные до (n+1) порядка включительно, на некотором промежутке,
содержащем точку х=а сделаем попытку найти многочлен Pn(x) степени не выше чем n,								значение которого в т.
х=а совпадает со значением функции f(x) в этой точке, а значения производных его до n							ого	порядка совпадают со
								порядка совпадают со

значениями производных от f(x) в точке х=а, т.е.

(a)=f(a); P

(x)=f '(a), ..., P(n) (a) = f

(n) (a)

(1)

При этих условиях многочлен Pn(x) в некотором смысле «близок» к функции f(x).

Многочлен Pn(x)

будем искать в форме многочлена по степеням (х-а)

c неопределенными

коэффициентами Ci ,

то есть

Pn(x)=C0+C1(x-a)+C2(x-a)2+...+Cn(x-a)n.

(2)

Неопределенные коэффициенты Ci в (2) определяются из условий (1):

Pn(a)=C0=f(a)

C0=f(a)

Pn(a)=C1=f (a)

C1=f (a)

Pn(a)=1 2 C2=f (a)

C2=

f (a)

(3)

Pn(a)=3! C3=f (a)

. . . . . . . . . . . . .

P(n) (a) =n! C = f

(n) (a)

C =

f (n) (a) .

Подставим значения Ci из (3)

в (2), тогда получим

f (a)

f (n)

(a)

P (x)=f(a)+f (a)(x-a)+

(x-a)2+...+

(x-a)n

(4)

Теперь оценим разность функций f(x) и построенного многочлена. Обозначим через Rn(x) разность f(x)

и Pn(x):

Rn(x)=f(x)-Pn(x).

Тогда f(x)=Pn(x)+Rn(x), причем имея ввиду (4), получим, что

f(x)=f(a)+f (a)(x-a)+

f (a)

fn(n) (a)

(х-а)

+...+

(х-а)

(x)

(5)

В формуле (5) Rn(x) называется остаточным членом и при достаточно малых функциях Rn(x)		на
некотором промежутке [ , ] э х многочлен Pn(x) дает приближенное представление о функции f(x).
То есть на этом промежутке [ , ] мы с достаточной точностью можем судить о функции f(x)		по
многочлену Pn(x).
Следующая наша задача заключается в оценке остаточного члена Rn(x).
Пусть Rn(x)=f(x)-Pn(x) или f(x)=Pn(x)+Rn(x).	(*)
Последняя формула называется формулой Тейлора для функции f(x) с остаточным членом Rn(x).
Выразим R (x) через (n+1)ую производную функции f(x) :
n

f (a)

f (n) (a)

(x-a)n,

т.к. Pn(x)=f(a)+

(х-а)+

(х-а)2+...+

то

R (а)=R (а)=...= R(n)

(а)=0

Возьмем функцию (х)=(х-а)n+1, для которой также имеет место

(а)= (а)=...= (n)(a)=0.

Применяя n раз теорему Коши для функций (x) и Rn(x) на промежутке

[x, a],

[x1, a]

и т.д., получаем

(x)

(x) R

(a)

(x )

R (x ) R

(a)

)

...

(x)

(x) (a)

(x )

) (a)

)

(n)

)

R(n) (x

) R(n) (a)

R(n 1) ( )

(n) (x

)

(n) (x

) (n) (a)

(n 1) ( )

(x)

R(n 1)

( )

R(n 1) ( )

(x a)n 1 f (n 1) ( )

Тогда

или Rn(x)=

; т.к.

(x)

(n 1)

( )

1)!

(n 1)!

R(n 1) (х)=f(n+1)(x) см. (*)

Окончательно получим:

f (a)

f (n) (a)

f (n 1) ( )

f(x)=f(a)+

(х-а)+...+

(х-а)n+

(x-a)(n+1)

(n 1)!

где =а+ (х-а); (0; 1).

Последняя формула называется формулой Тейлора с остаточным членом в форме Лагранжа. (разложение функции в окрестности точки а или по степеням х-а). Эта формула при а=0 называется формулой Маклорена.

Доказанное можно сформулировать в виде теоремы:

Если f(x) имеет в окрестности точки х=а непрерывную производную f(n+1)(x), то для любой точки х из

(k)

(a)

(n 1)

( )

этой окрестности имеет место формула Тейлора, т.е. f(x)=

(х-а)k+

(x-a)(n+1).

(n 1)!

k 0

2. Разложение основных функций по формуле Тейлора

в окрестности точки х=0.

1. у=ех.

x(n 1)

(n)

=1, то у=ех=1+х+ x

... x

n 1

Так как (e

)x 0

, где (0; 1).

n! (n 1)!

Очевидно, что Rn(x) 0

при n и хR. Оценим далее Rn(x) на промежутке |x| 1

и n=5:

xn 1e x

|R5(x)|=

(n 1)!

240

(5 1)!

Таким образом, ошибка вычисления ех при |x| 1 и n=5 по формуле

ех 1+х+

не превосходит

. Выбирая больше чем 5 значение n в формуле

240

получим более точное значение функции ех.

Пример. Полагая в разложении ех х=1, n=5,

получим

е1+1+

2,717

120

2. у=sin x

(n)

=Sin n /2,

(n 1)

=sin( +(n+1) /2)

Так как (sin x)

х 0

а (sin x) x

получим

разложение

х3

х5

х7

xn 1

у=sin x=x-

...

sin n

sin(

)

(n 1)!

Оценка остаточного члена формулы:

\|R (x)\|=\|		xn 1		sin( +(n+1) /2)\| \|			xn 1

n		(n	1)!				(n 1)!

Заметим, что Rn(x) 0					при n и x R.
3. у=cos x
	(n)			n		(n 1) =cos
(cos x)			=cos		и (cos х)
	х 0			2		x

y=cos x=1- x2 x4 ... xn cos n 2! 4! n! 2

n
		n 1 ;
	2

xn 1		1 n
	cos(		) .

(n 1)!		2

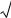
Очевидно здесь R (x)=

xn 1

cos(

1 n

) 0, при n и любых x R.

(n 1)!

y=ln(1+x)

Так как (ln(1+x))(n)=(-1)n-1

(n 1)!

(n)

=(-1)n-1(n-1)!, то получим

; (ln(1+x)) х

(1 x) n

разложение при х(-1; 1):

ln(1+x)=x-

х2

х3

-...+(-1)n-

x n

+R (x)

Rn(x)=

( 1)n xn 1

. Если х(-1; 1), то Rn(x) 0

при х

1)(1 x)n 1

5. у=(1+х)m

Формула Тейлора для этой функции при х(-1; 1) имеет вид:

y=(1+x)m=1+mx+

m(m 1)

x2 ...

m(m 1)...(m n 1)

xn +R (x).

Например:

1 x

+R3(x) Здесь записано лишь три члена разложения

3. Применение формулы Тейлора.

0(x4 ) x

sin x x

lim

= lim

=-1/6.

х 0

cos x

1 x2

0(x6) 1 x2

0(x

3! 8

lim

2! 4

x 0

sin x

x 0

1 1

tgx x

lim

0(x

) x

ctgx

xtgx

x 0 x x

x 0 x

tgx

4. Ряд Тейлора функции одного переменного.

Как нетрудно заметить, сумма всякого степенного ряда является некоторой функцией, определенной внутри круга сходимости этого ряда.

В связи с этим возникает одна из важных задач теории рядов: по заданной функции найти степенной ряд, сумма которого в области сходимости равнялась бы данной функции.

Оказывается этот ряд имеет вид

	f (n) (a)		f (a)		f (n) (a)
		(x-a)n f(a)+f (a)(x-a)+		(х-а)2+...+		(х-а)n+...
	n!	(x-a)n f(a)+f (a)(x-a)+	2!	(х-а)2+...+	n!	(х-а)n+...
n 0	n!		2!		n!

и называется рядом Тейлора для функции f(x) в окрестности точки х=а. Замечание. Если а=0, то ряд Тейлора называется рядом Маклорена. Особо отметим два различных понятия:

1) Остаточный член формулы Тейлора

Rn(x) f(x)-[f(a)+f (a)(x-a)+ f (a) (x-a)2+...+ f (n) (a) (x-a)n] f(x)-Sn(x), который определяется для всякой

2! n!

достаточно много раз дифференцируемой функции f(x) .

2) Остаточный член ряда Тейлора:

R*n(x)=S(x)-[f(a)+f (a)(x-a)+..+ f (n) (a) (x-a)n] S(x)-Sn(x), который определяется для бесконечно

дифференцируемой функции f(x). Здесь S(x) - сумма ряда Тейлора для функции f(x) и Sn(x) - n ая частичная сумма

этого ряда.

Оба остаточных члена равны между собой, если S(x)=f(x), то есть если ряд Тейлора сходится к функции f(x), для которой он построен.

	f	(n)	(a)
Теорема. Ряд Тейлора				(х-а)n, построенный для функции f(x), сходится к ней в некоторой

		n!
n 0

окрестности точки х=а, в том и только в том случае, если последовательность Rn(x) остаточных членов в формуле Тейлора стремится к нулю при n в этой окрестности, т.е.

Rn(x)=f(x)-[f(a)+f '(a)(x-a)+...+

Доказательство.

f (n) (a) (x-a)n] 0 при n .

Так как f(a)+f (a)(x-a)+...+			f (n) (a)		(x-a)n=S (x)		-	nая частичная сумма ряда Тейлора для функции f(x) , то при
Так как f(a)+f (a)(x-a)+...+					(x-a)n=S (x)		-	nая частичная сумма ряда Тейлора для функции f(x) , то при
				n!		n
				n!
Rn(x) 0 имеем
lim	R (x)=	lim (f(x)-S		(x))=0, то есть		lim	S (x)=f(x) или S(x)=f(x).
n	n	n		n	n n
Обратно: если lim S (х)=f(x), то					lim	R (x)=		lim	(f(x)-S (x))=0.
		n n			n	n		n	n

Теорема. Если функция f(x) имеет производные любого порядка в окрестности точки х=а и все они ограничены, то ряд Тейлора для функции f(x) сходится к этой функции в окрестности точки х=а, т.е. суммой ряда Тейлора

	f	(n)	(a)
				(x-a)n	будет сама функция f(x).

		n!
n 0

Замечание. При высказанных условиях можно доказать Rn(x) 0 при n .

5. Примеры.

1. у=ех.

Составим для ех ряд Тейлора-Маклорена в окрестности точки х=0:

...

ex~1+

(**)

n 0

e x xn 1

Составим Rn(x) формулы Тейлора:

Rn(x)=

, [0; 1].

(n 1)!

Очевидно, что

lim R (x)=0 при любых хR, то есть ряд (**) сходится к ех при любом значении х из R. В силу

этого можно писать ех=1+х+

...

n 0

2. у=е-х.

n 1

-х

n x

- х

(-1)

, R (x)=(-1)

lim

R (x)=0 при хR.

n 0

(n 1)!

Значит Rcx=+ .

( 1)k x2k 1

xn 1 sin( x (n 1) )

sin x=

; R (x)=

; R

=+ .

n 0

(2k 1)!

(n 1)!

xn 1соs( x n )

cos x=

(-1)k

; R (x)=

; R

=+ .

n 0

(2k)!

(n 1)!

ch x=

ех е х

=1/2(

(-1)n

; R

=+ .

n 0

(2k)!

sh x=

ех е х

2k 1

=1/2(

- (-1)n

;

R =+ .

n 0

(2k

1)!

n 1

ln(1+x)=

(-1)n

;

=1.

n 0

n 1

...=

2k 1

arctg x=x-

(-1)n

;

=1.

n 0

1 3 5 ... (2n 1) x2n 1

arcsin x=

;

Rcx=1.

4 ... (2n)

2n 1

n 0

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2625 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.20151.1 Mб125Лекции-История и методология языкознания.doc
#
03.05.2015366.08 Кб154Лекции-ст.doc
#
13.08.201973.73 Кб7Лекции.doc
#
09.11.20184.19 Mб46лекции.doc
#
27.03.2015223.47 Кб36Лекции.docx
#
27.03.20154.74 Mб73ЛЕКЦИИ_ПО_ВЫСШЕЙ_МАТЕМ_Голубев.pdf
#
27.03.2015274.94 Кб7Лекции_по_ИЭ_2.doc
#
11.03.20162.17 Mб26Лекции_тервер.pdf
#
27.03.20153.81 Mб123ЛекцииМО.doc
#
27.03.2015473.6 Кб10Лекционный курс для подготовки (студентам).doc
#
27.03.2015222.15 Кб17Лекция 02 Кинематика криволинейного движения..pdf