простейшем случае [3] рассчитывают путем подстановки в (9.5) или (9.20) амплитудно-фазового распределения возбуждения в виде

a(z)=a0expi[ψ(z)–ηγz],

где ψ(z) – стационарный случайный процесс с нулевым средним значением и известной величиной дисперсии α=ψ2 (z) . Обычно α<<1. Структурная функция, т. е. средний квадрат разности фаз между двумя любыми точками z1 и z2 , зависит только от расстояния ∆z =z1 −z2 по закону

K(z1,z2 )=[ψ(z1)−ψ(z2 )]2 =α[1−exp(−∆z2 /ρ2 )] ,

где ρ – характерный размер, называемый радиусом корреляции. Из формулы следует, что среднеквадратическая разность фаз между точками, разнесенными на расстояние ρ, составляет около

0,79 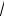α рад, т. е. случайные отклонения фазы в этих точках почти не коррелированы между собой.

Каждой реализации возбуждения соответствует реализация множителя направленности антен-

ны

L/2

fc (θ)=a0 ∫expi[γz(cosθ−ξ)+ψ(z)]dz .

−L/2

Если произвести усреднение по большому числу реализаций множителя направленности (усреднение по ансамблю), то можно установить зависимость средних параметров линейной антен-

ной системы от величины дисперсии фазовых ошибок α и радиуса корреляции ρ. После этого рассчитывают следующие характеристики:

•форму средней диаграммы направленности;

•среднее значение КНД в направлении максимума излучения;

•наиболее вероятный уровень боковых лепестков.

9.3.Плоские излучающие системы

9.3.1. Основные определения и исходные соотношения

Линейная система излучателей позволяет получить антенну с узкой ДН только в одной плоскости, которая проходит через ось решетки. Чтобы сузить луч антенны и в другой плоскости, т. е. сформировать игольчатую ДН, необходимо разместить излучающую систему в простейшем случае на плоской поверхности, выбрав ее размеры достаточно большими в сравнении с длиной волны. Таким образом, мы приходим к остронаправленной антенне в виде непрерывного или дискретного распределения источников электромагнитного поля в пределах плоской поверхности (раскрыва). Форма раскрыва может быть произвольной: прямоугольной, круглой, эллиптической и т. д.

89

Рис. 9.17

ся математической сложностью и применяется редко.

Значительно проще апертурный метод, при котором предполагают, что токи на внешней поверхности S2 ничтожно малы. Это предположение тем более обосновано, чем больше размер раскрыва по сравнению с длиной волны. Таким образом, расчет поля апертурной антенны сводится к основанному на принципе Гюйгенса расчету поля источников, расположенных в ее раскрыве. Из этого принципа следует, что каждый элемент поверхности раскрыва можно рассматривать как элементарный источник электромагнитных волн – излучатель Гюйгенса. Составляющие поля излучения этого источника определяются по формулам (7.34).

Пользуясь этими формулами и производя интегрирование по раскрыву, можно определять поле излучения, т. е. решать апертурным методом так называемую внешнюю задачу электродинамики. Однако чтобы решить эту задачу, нужно знать распределение амплитуд, фаз и поляризации поля в раскрыве. Нахождение этого распределения при заданном первичном источнике возбуждения составляет так называемую внутреннюю задачу, которая часто оказывается более сложной, чем внешняя, и решается методом геометрической оптики.

Для получения наибольшего коэффициента направленного действия плоского раскрыва стремятся сделать распределение поля в нем синфазным. Иногда это не удается выполнить из-за неточностей в изготовлении антенны или ее конструктивных особенностей. В ряде случаев несинфазность создается умышленно для получения ДН специальной формы. Амплитудное распределение поля в раскрыве в общем случае является неравномерным. Поляризация поля в разных точках раскрыва может быть различной, однако электрический вектор в каждой точке можно разложить на две компоненты, например (рис.9.18) параллельные координатным осям, а затем найти поле излучения, обусловленное каждой из этих компонент. Поэтому, не уменьшая общности рассуждений, можно считать, что в плоском раскрыве S произвольной формы, лежащем в плоскости хоу, электрический вектор Es всегда параллелен оси х (рис.9.18). Выберем на раскрыве элементарную площадку dS. Рассматривая ее как излучатель Гюйгенса и полагая, что характеристическое сопротивление волны, набегающей на раскрыв первичного источника, равно 120π, выразим меридиональную и азимутальную составляющие поля излучения этой площадки формулами (7.35).

x

ϕ

Здесь R – расстояние от площадки dS до точки М, расположенной в дальней зоне; θ и ϕ – угловые координаты точки М в сферической системе координат, начало которой совпадает с серединой S. Составляющие полного поля излучения определяются интегрированием по раскрыву:

90