
Электромагнетизм
.pdf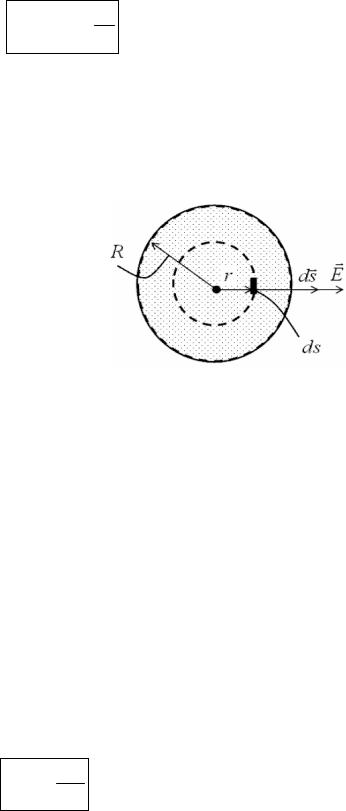
Таким образом, поле бесконечного плоского конденсатора сосредоточено внутри, между его пластинами, и равно
Eпл.конд = εσ
0
(Примечание: конденсатор можно считать бесконечным, если размеры пластин примерно на порядок больше расстояния между ними).
Поле объемно-заряженного шара Пусть имеется равномерное скопление зарядов в виде шара
(рис. 16.9) радиусом R с объемной плотностью ρ ([ρ]= Кл/м3 ). Поле шара обладает центральной симметрией.
Записываем теорему Гаусса ∫ Eds = |
∑ qi |
. |
|
ε0 |
|||
s |
|
Проведем внутри шара вспомогательную (гауссову) поверхность в форме сферы радиусом r . Дальнейшие преобразования: ∫ Eds = ∫ Edscosα = ∫ Eds . Напряженность
s s s Рис. 16.9
по величине на одном и том же расстоянии r
от центра шара одинакова, поэтому, вынося E за знак интеграла, получим:
∫ Eds = E∫ds = E4πr2 , s s
где 4πr2 – площадь гауссовой сферы.
Заряд, охватываемый гауссовой поверхностью, равен ρ43 πr3, где
43 πr3 – объем шара.
В итоге, подставляя Е4πr2 в левую часть, а ρ43 πr2 – в правую часть
теоремы Гаусса, получаем: E4πr2 = |
ρ |
4 |
πr3 |
|
|
||||
3 |
|
и поле внутри заряженной сферы |
||
|
|
|||
|
|
ε0 |
||
E(r) = ρr
3ε0
11

Проведя аналогичные действия вне заряженной сферы, нетрудно получить
E(r) = ρR3
3ε0r2
График зависимости E(r) представлен на рис. 16.10.
4. Теорема Гаусса в дифференциаль-
Рис. 16.10 ной форме. Введем понятие объемной плотности заряда ρ = dVdq аналогично плот-
ности массы. Чтобы найти суммарный заряд, заключенный внутри замкнутой поверхности s , нужно вычислить интеграл от ρ по объему V, ограниченному
n
поверхностью, Q = ∑qi = ∫ρdV , т.е. можно записать теорему Гаусса i=1 V
∫ Eds = |
1 |
∫ρdV . |
|
||
s |
ε0 V |
|
Воспользуемся теоремой Остроградского – Гаусса (Михаил Васильевич Остроградский – крупнейший русский математик, академик, 1801 – 1861 гг.) (без вывода)
∫ Eds = ∫divE dV
s V
где divE – дивергенция напряженности электрического поля. (По опреде-
лению дивергенции divE = ∂∂Exx + ∂∂Eyy + ∂∂Ezz ).
Тогда очевидно равенство
1 |
∫ρdV = ∫divE dV |
(*). |
|
|
|||
ε0 V |
V |
|
|
Из выражения (*) следует теорема Гаусса в дифференциальной форме
divE = ρ
ε0
12
Для уяснения смысла дивергенции проведем параллель с текущей жидкостью. Известно, что div υ– удельная мощность источников жидкости в данной точке (υ – вектор скорости). По аналогии говорят, что заряды являются источниками электрического поля.
Вопросы для самоконтроля
1.Сформулируйте закон Кулона.
2.Что такое напряженность электрического поля?
3.В чем заключается принцип суперпозиции электрических полей?
4.Что такое силовые линии? Для чего они используются?
5.Дайте определение потока напряженности электрического поля через элементарную площадку. Как определяется полный поток напряженности через произвольную поверхность?
6.Сформулируйте теорему Гаусса и осуществите ее вывод.
7.Решите самостоятельно задачи на применение теоремы Гаусса.
13
Лекция № 17
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
План
1.Работа сил электростатического поля. Потенциальность (консервативность) электростатического поля. Циркуляция вектора напряженности электростатического поля.
2.Потенциал. Разность потенциалов. Связь между потенциалом и напряженностью электростатического поля.
3.Электрический диполь. Дипольный момент. Потенциал диполя. Момент сил, действующихна диполь вовнешнем электростатическом поле.
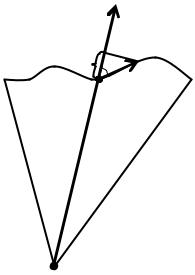
1. Работа сил электростатического поля. Работа силы F , совер-
шаемая при перемещении dl материальной точки под действием этой силы, равна dA = Fdl = Fdlcosα, где α – угол между направлением силы и
|
F |
|
направлением перемещения. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Пользуясь этой формулой, можно найти |
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
dr α |
|
работу по перемещению одного заряда в поле |
||||||||||||||||||||||||
1 |
2 другого неподвижного заряда (рис. 17.1). |
|
|
|
|||||||||||||||||||||||
|
dl |
|
|
Заряд q1 |
перемещается из точки 1 в точ- |
||||||||||||||||||||||
|
q1 |
|
|
||||||||||||||||||||||||
|
|
|
|
ку 2 в поле заряда q . Элементарная работа си- |
|||||||||||||||||||||||
|
r |
|
лы F на перемещении dl равна |
|
|
|
|
|
|
||||||||||||||||||
r1 |
|
|
|
|
|
|
dA = Fdl = Fdlcosα = Fdr . |
|
|
|
|
|
|
||||||||||||||
|
r2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Так как сила F = |
|
qq1 |
|
, то полная ра- |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
4πε0r2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
бота на пути |
|
из |
точки 1 |
в |
точку |
2 |
равна |
||||||||||||||||
|
q |
|
|
r2 |
|
|
|
r2 |
|
r2 |
|
qq1 dr |
|
qq1 |
1 1 |
|
|||||||||||
|
|
|
|
A12 = ∫dA = |
∫ Fdr = ∫ |
|
|
|
2 |
= |
|
|
|
|
− |
|
, |
||||||||||
|
|
|
|
4πε |
0 r |
4πε |
0 |
r |
r |
||||||||||||||||||
|
Рис. 17.1 |
|
|
|
r1 |
|
|
|
r1 |
|
r1 |
|
|
|
|
|
1 |
2 |
|
||||||||
|
|
то есть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A12 = |
qq1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4πε |
0 |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Потенциальность (консервативность) электростатического поля. Циркуляция вектора E . Из формулы (*) видно, что A12 не зависит от пути перемещения заряда q1 и определяется только относительными положениями q и q1 в начале и конце пути. Отсюда, в частности, следует, что работа по перемещению заряда q1 по замкнутому контуру равна нулю, то есть электростатическое поле является потенциальным.
Элементарную работу dA можно записать в форме dA = Fdl = q1Edl ,
где E – вектор напряженности поля, создаваемого зарядом q . Работа по замкнутому контуру равна
∫dA = ∫q1Edl = q1 ∫ Edl .
Выражение ∫Edl называется циркуляцией вектора E по замкнутому контуру. Для электростатического поля работа по замкнутому контуру из формулы (*): ∫dA = 0 , отсюда ∫dA = ∫q1Edl = q1 ∫ Edl = 0 , то есть
∫ Edl = 0
Таким образом, условием потенциальности электростатического поля является равенство нулю циркуляции вектора напряженности электростатического поля E по любому замкнутому контуру.
2. Потенциал. Разность потенциалов. Тело, находящееся в потен-
циальном поле, имеет потенциальную энергию. Работу по перемещению тела можно представить в виде разности потенциальных энергий в начале и конце пути
A12 =Wp1 −Wp2 |
|
qq1 |
|
1 |
1 |
|
|
qq1 |
|
|
qq1 |
|||||
= |
|
|
|
|
− |
|
|
= |
|
|
|
− |
|
|
. |
|
4πε |
0 |
r |
r |
4πε |
0 |
r |
4πε |
r |
||||||||
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
0 2 |
|
|||
Потенциальную энергию можно отсчитывать от любого уровня (так как физический смысл имеет только лишь разность потенциальных энер-
15
гий). Удобно выбрать потенциальную энергию заряда на бесконечности за начало отсчета потенциальной энергии.
Устремим r → ∞, тогда |
A |
=W |
p |
= |
|
qq1 |
, а в общем случае |
|
|||
|
|
|
|
||||||||
2 |
1∞ |
|
|
|
4πε0r |
|
|||||
|
|
|
|
|
1 |
|
|
||||
|
|
Wp = |
|
qq1 |
|
|
|
|
(**) |
||
|
|
4πε0r |
|
|
|||||||
|
|
|
|
|
|
||||||
где Wp – потенциальная энергия заряда q1 в поле заряда q на расстоянии r . Определение. Потенциал ϕ – это энергетическая характеристика элек-
тростатического поля, скалярная величина, численно равная отношению потенциальной энергии, которую имеет заряд в данной точке поля, к величине этого заряда.
ϕ = Wp q1
Подставляя выражения для потенциальной энергии (**) в (***), получим формулу для потенциала электростатического поля точечного заряда
ϕ = 4πεq0r
Единица измерения потенциала – вольт. [ϕ]=1 В.
В силу введенного определения потенциала ϕ работа по перемеще-
нию заряда q1 в электростатическом поле из точки 1 в точку 2 |
|
|
||||||||||||||
A12 =Wp1 −Wp2 = |
qq1 |
|
− |
qq1 |
= q1 |
|
q |
− |
q |
|
= q1(ϕ1 |
−ϕ2) , |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
4πε |
0 |
r |
4πε |
r |
4πε |
r |
4πε |
r |
||||||||
|
|
1 |
|
|
0 2 |
|
|
|
0 1 |
|
|
0 2 |
|
|
|
|
откуда
A12 = q1(ϕ1 −ϕ2) ,
(В дифференциальной форме dA = −q1dϕ). Разность потенциалов то-
чек 1 и 2:
ϕ1 −ϕ2 = A12
q1
16

Разность потенциалов – отношение работы по перемещению заряда к величине этого заряда, удельная работа кулоновских сил, однозначно определяемая начальной и конечной точками перемещения.
Связь между потенциалом и напряженностью электростатиче-
ского поля. Для работы на перемещении dl можно написать два эквивалентных выражения.
dA = q1Edl
dA = −q1dϕ
Знак « – » во второй формуле связан с тем, что работа сил поля над зарядом равна убыли потенциальной энергии заряда.
Сравнение двух формул приводит к связи между потенциалом поля ϕ и вектором напряженности электростатического поля E .
Edl = Exdx + Eydy + Ezdz = −dϕ.
Отсюда
Ex = −∂ϕ ; |
Ey = − |
∂ϕ ; Ez = −∂ϕ. |
|
|
|
||
|
∂x |
|
∂y |
∂z |
|
|
|
Вектор E можно представить как E = Exex + Eyey + Ezez , подставляя |
|||||||
выражения для компонент вектора E , получим: |
|
|
|
|
|||
E = −∂ϕex − |
∂ϕey − |
∂ϕez = − ∂ϕex + |
∂ϕey |
+ |
∂ϕez |
||
∂x |
∂y |
∂z |
∂x |
∂y |
|
∂z |
|
Выражение в скобках есть не что иное, как grad ϕ, окончательно получаем
E = −gradϕ
17
Напряженность поля E равна градиенту потенциала, взятому со знаком минус.
(Примечания. 1. Используя символ «набла» ϕ = ∂∂ϕx ex + ∂ϕ∂y ey + ∂ϕ∂z ez ,
связь между вектором напряженности E и потенциалом ϕ можно представить более компактно
E= − ϕ
2.В случае радиальной симметрии E = − ddrϕ ).
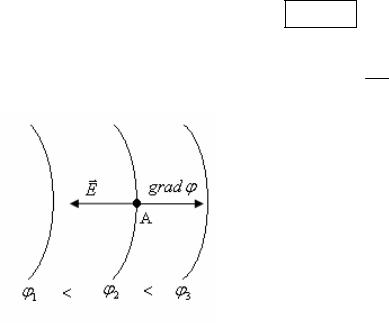
Пример: Пусть имеются эквипотенциальные линии (линии одинакового потенциала) ϕ1, ϕ2 и ϕ3 причем ϕ1 < ϕ2 < ϕ3 (рис. 17.2). Требу-
ется указать направления векторов gradϕ и E
в некоторой точке А. В соответствии с определением градиента он направлен в сторону бы-
стрейшего возрастания ϕ, то есть по перпен-
Рис. 17.2
дикуляру к касательной в точке А к эквипо-
тенциальной линии ϕ2 в сторону ϕ3. Из формулы связи E и ϕ следует,
что вектор E направлен в противоположную сторону.
3. Электрический диполь. Дипольный момент. Потенциал диполя.
Электрическим диполем называют систему двух одинаковых по величине разноименных точечных зарядов + q и − q , расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя (рис. 17.3).
18
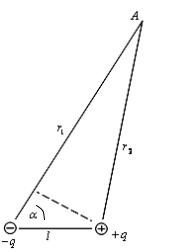
В соответствии с принципом суперпозиции потенциал поля в некоторой
|
q |
|
q |
|
1 |
|
|
q |
|
|
q |
|
|
|
|
точке А равен ϕдип =ϕ1 +ϕ2 =− |
+ |
= |
|
q |
− |
|
= |
r1 −r2 |
. |
||||||
|
4πε0r2 |
|
|
|
|
||||||||||
|
4πε0r1 |
|
4πε0 r2 |
|
r1 |
|
4πε0 |
r1r2 |
|||||||
|
Пусть точка А выбрана так, что длина l намного меньше расстояний |
||||||||||||||||||||||||
r |
и r . В этом случае можно положить, что r |
−r =lcosα; r r ≈ r2 |
и фор- |
||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 2 |
|
|
|
||||||
мулу для потенциала диполя ϕдип можно переписать: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
qlcosα |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
ϕдип = |
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4πε0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где α – угол между осью диполя и направле- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
||||||||||
нием к точке А, проведенным от диполя. Про- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
изведение p = ql |
называется электрическим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
моментом диполя, или дипольным моментом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Вектор p |
направлен по оси диполя от |
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
||||||||||||
отрицательного заряда к положительному. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, |
произведение ql в формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
α |
|
|
|
|
|
|
|
|
|
|||||||||||||
для ϕдип является дипольным моментом |
p и |
|
|
|
|
|
|
|
|
|
|
|
|
+ q |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
l |
|
||||||||||||||||
|
−q |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 17.3 |
|
||||||||
|
|
ϕдип = |
p cosα |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
4πε0r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Потенциал поля диполя пропорционален дипольному моменту |
p , ко- |
|||||||||||||||||||||||
синусу α и обратно пропорционален квадрату расстояния от диполя до рассматриваемой точки, то есть потенциал диполя убывает быстрее с рас-
|
~ |
1 |
стоянием, чем потенциал точечного заряда |
. |
|
|
|
r |
Момент сил, действующих на диполь во внешнем электрическом поле. Поместим диполь в электрическое поле (рис. 17.4). Пусть направление диполя составляет с направлением вектора напряженности E некоторый угол α. На отрицательный заряд действует сила F1 = −qE , направлен-
19
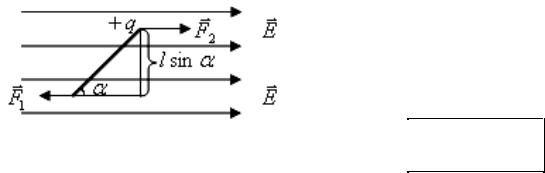
ная против поля, на положительный заряд действует сила F2 = qE , направленная вдоль поля.
Эти силы образуют пару сил с вращающим моментом
M = Flsinα = qElsinα = pEsinα.
В векторном виде
Рис. 17.4 |
|
|
M вр = p × E |
||
Диполь в однородном внешнем поле поворачивается под действием вращающего момента таким образом, чтобы сила, действующая на положительный заряд диполя, совпадала по направлению с вектором E и осью диполя. Этому положению соответствуют α = 0 и Мвр = 0 .
Вопросы для самоконтроля
1.Как вычислить работу, совершаемую над точечным зарядом при его перемещении в электрическом поле? Зависит ли эта работа от формы траектории?
2.Что такое потенциал электростатического поля? Запишите его выражение для точечного заряда.
3.Какова связь потенциала с напряженностью электростатического поля?
4.Что такое электрический диполь? Дипольный момент?
5.От чего зависит потенциал поля диполя?
6.Вычистите момент сил, действующих на диполь во внешнем электрическом поле.
20
