Смирнов Стат Физ

При нормальных колебаниях смещение атома (n, α) имеет вид

qn,α = Uα exp(i(kan − ωt)),

где ω одинаковая для всех атомов угловая частота колебаний, t время. Фазы трансляционно-эквивалентных атомов (с одним и тем же α) определяют-

ся вектором k, который носит название волнового вектора. Амплитуды Uα трансляционно-эквивалентных атомов одинаковы.

В силу дискретности кристаллической решетки возможные значения волновых векторов оказываются ограниченными некоторой областью в пространстве волновых векторов, называемой первой зоной Бриллюэна.

Наряду с векторами прямой решетки ai введем в рассмотрение три основных вектора обратной решетки

целочисленная линейная комбинация которых образует вектор произвольной трансляции обратной решетки

Концы этих векторов, отложенных от одной точки, и образуют саму обратную решетку. Векторы ai (i = 1, 2, 3) è Bj (j = 1, 2, 3) обладают свойствами

Оно кратно 2π. Поэтому

exp(i(an · Bm)) = 1.

Наложим периодические граничные условия:

qn+Niai,α = qn,α

èëè

Если представить k в виде разложения по векторам обратной решетки

k = k1B1 + k2B2 + k3B3,

60

то из (76) следует, что ki = mi/Ni. В силу свойств (75) k можно считать принимающим значения только в пределах одной элементарной ячейки обратной решетки. Принято выбирать для k элементарную ячейку в виде многогранника, равновели-

кого параллелепипеду, построенному на основных векторах обратной решетки Bi. Этот многогранник называют, как это было отмечено выше, первой зоной Бриллюэна (ЗБ). Для его построения проведем из начала координат (в пространстве векторов k) все векторы обратной решетки (74). Затем через их середины пер-

пендикулярно векторам проведем плоскости. Многогранник вблизи начала координат, ограниченный ближайшими плоскостями и называется первой ЗБ. Внутри ЗБ нет двух точек, отличающихся друг от друга на вектор обратной решетки (как и в элементарной ячейке, выбранной любым другим образом). Первая ЗБ имеет точечную симметрию кристаллической решетки (симметричная элементарная

ячейка). Граничным условиям удовлетворяют только N = N1N2N3 векторов k из ÇÁ. Òàê êàê ki = Ni−1, то при больших Ni волновой вектор можно считать меняющимся почти непрерывно (квазинепрерывным).

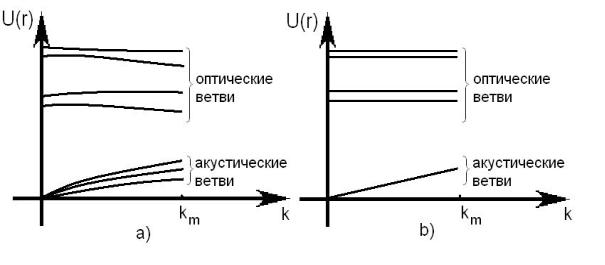
Решение механической задачи о колебаниях решетки приводит к тому, что при каждом k существует 3σ нормальных колебаний с частотами ωj(k). При фиксированном j малому изменению k соответствует малое изменение частоты ωj(k). Îá ωj(k) при фиксированном j говорят как о ветви колебаний. Всего имеется 3σ ветвей. На рис. 13a изображен типичный ход ωj(k) вдоль одного из направлений в k-пространстве. Из 3σ ветвей 3 ветви называются акустическими. Для

íèõ ωj(k) → 0 при k → 0. Остальные ветви называются оптическими (ветви оптических колебаний). Для них ωj(q) → ωj(0) ïðè k → 0.

Ðèñ. 13: a) Колебательные ветви ωj(k) вдоль одного из направлений в k-про- странстве. b) Аппроксимация колебательных ветвей по Дебаю и Эйнштейну.

Текущие координаты атома запишем в виде

rn,α = an + dα + qn,α.

qn,α вектор, определяющий смещение атома из положения равновесия. Совокупность 3σN смещений qn,α,i обозначим q.

61

При рассмотрении малых колебаний решетки в исходной функции Гамильто-

íà

p2

H = X n,α,i + W (q)

n,α,i 2mα

потенциальную энергию W (q) разложим по степеням малых смещений qn,α,i

как в положении равновесия сила, действующая на любой атом, равна нулю. Функция Гамильтона с точностью до квадратичных членов по смещениям примет вид

Этой функции Гамильтона соответствуют уравнения движения

n,α,i

Сначала получим решения частного вида нормальные колебания

qn(k,α,i,j) = √mαUα,i(j)(k) exp(i(k · an − ωj(k)t)).

n

Затем можно построить общее решение системы (77)

qn,α,i = X Qj(k)Uα,i(j)(k) exp(i(k · a)n − ωj(k)t).

j,k

62

Совершив каноническое преобразование к новым координатам Qj(k) и импульсам Pj(k) (их называют нормальными), получим функцию Гамильтона в новых переменных

H(Q, P ) = X Hj,k, Hj,k = 12[Pj2(k) + ωj(k)Q2j (k)].

j,k

Такая структура функции Гамильтона указывает на то, что колеблющаяся кристаллическая решетка в квадратичном приближении по смещениям может рассматриваться как система независимых осцилляторов (j, k).

Согласно классической статистике каждому осциллятору во внутренней энергии соответствует вклад kT . Поэтому внутренняя энергия решетки E = 3σNkT ,

а теплоемкость CV,N = 3σNk. Для одноатомных кристаллов CV,N = 3Nk. Для грамм-молекулы вещества CV,N = 3NAk (NA = 6.02 × 10−23 число Авогадро).

Это закон Дюлонга и Пти, оправдывающийся только при высоких температурах. При низких температурах нужно учитывать квантовые эффекты.

Согласно квантовой механике осциллятор (j, k) с частотой ωj(k) в состоянии с квантовым числом nj,k имеет энергию

Enj,k = ~ωj(k)(nj,k + 1/2), nj,k = 0, 1, 2, ... .

Состояние всей системы невзаимодействующих осцилляторов (идеальный газ), моделирующих кристаллическую решетку, задается совокупностью 3σN чисел {nj,k}, а соответствующая ему энергия

X

E{nj,k} = Enj,k.

j,k

Как всегда в случае идеального газа статсумма всей системы выражается через статсуммы отдельных осцилляторов

Первая сумма дает наименьшую энергию решетки Eo, когда все осцилляторы на- ходятся в своих самых нижних по энергии состояниях. Рассмотрим вторую сумму.

63

Точки k распределены равномерно по ЗБ. На каждое из N состояний приходится

Дальнейшие вычисления требуют знания зависимостей ωj(k). Рассмотрим простейшую модель. Для оптических ветвей примем ( приближение Эйнштейна, см. рис. 13b):

Введем обозначения Toj = ~ωj(o)/k (j = 4, 5, ..., 3σ). Тогда вклад оптических ветвей во внутреннюю энергию будет

Для всех трех акустических ветвей примем один и тот же линейный закон дисперсии (приближение Дебая, см. рис. 13b)

ωj(k) = vk, j = 1, 2, 3.

При интегрировании по k в вычислении вклада акустических ветвей в энергию

воспользуемся сферической системой координат и заменим интегрирование по ЗБ интегрированием по равновеликой сфере (радиуса km):

g(ω)dω число состояний в частотном интервале dω. В трех акустических ветвях имеется 3N состояний. Поэтому

Таким образом

64

Введем новую переменную x = (~ω/kT ) и так называемую температуру Дебая TD = ~ωm/k. Тогда вклад акустических ветвей в энергию примет вид

Eac = 3NkT D(TD/T ),

где D(y) функция Дебая:

Рассмотрим предельные случаи.

Случай высоких температур T TD, Toj, TD/T = y 1, При малых y функция Дебая

Рис. 14 показывает ход теплоемкости одноатомного кристалла в рассмотренной модели. В реальных кристаллах зависимости ωj(k) более сложные, но каче- ственно ход теплоемкости сохраняется таким же.

Температуры Дебая могут варьироваться в широких пределах (см. таблицу 3).

65

Ðèñ. 14: График зависимости теплоемкости одноатомного кристалла от безразмер-

T

ной температуры TD .

Таблица 3: Температуры Дебая TD для некоторых кристаллов

4Флуктуации физических величин

В общем случае функция распределения ρ для системы, находящейся в некотором вообще говоря неравновесном состоянии, кроме координат q и импульсов p зависит от макроскопических параметров λ, определяющих ее состояние, и от времени t: ρ = ρ(q, p, λ; t). Физическая величина A в классической механике это некоторая функция координат, импульсов и времени: A = A(q, p; t). В различных системах статистического ансамбля физическая величина принимает различные значения a

и может быть рассматриваема как случайная величина. Функцию распределения ρA(a, t) для значений этой случайной величины можно найти, если известна функция распределения ρ = ρ(q, p, λ; t) систем ансамбля по микросостояниям:

Z

ρA(a, t) = δ(a − A(q, p; t))ρ(q, p, λ; t)d .

Эта функция распределения естественно нормирована на 1:

ZZ

1

Пусть, например, ρ = ρEo (q, p, ; V, N) = g(Eo, V, N)δ(Eo − H(q, p)) функция

66

микроканонического распределения, а физическая величина полная механиче- ская энергия E = H(q, p). Тогда

Z

1

ρEo = g(Eo, V, N)δ(E − H(q, p))δ(Eo − H(q, p))d =

Z

1

g(Eo, V, N)δ(E − H)δ(Eo − H)g(H)dH = δ(E − Eo).

Получаем естественные для этого случая результаты:

Z

E = Eδ(E − Eo)dE = Eo, E2 = Eo2, (ΔE)2 = 0.

4.1Флуктуации энергии и температуры

Обозначим β = (kT )−1. Для среднего значения и дисперсии энергии получаем

Применение квантового канонического распределения дает тот же результат. Примеры.

1. Одноатомный идеальный газ (см. разделы 2.7 и 2.12).

67

2. Равновесное излучение. Из (66) и (65) получаем для относительной флуктуации энергии

√

δE = 2 30.6N−1/2. π2

3. Кристаллическая решетка. При высоких температурах из (79) и (78) находим для относительной флуктуации энергии (напомним, что σ число атомов в

элементарной ячейке, N число ячеек в решетке, число атомов в решетке σN)

а при низких температурах из (80) и (81)

Эти частные случаи иллюстрируют общее положение, касающееся зависимости относительной флуктуации аддитивной физической величины от числа частиц в системе (см. раздел 2.7).

Если система сохраняет объем и число частиц, то с макроскопической точки зрения изменение внутренней энергии связано с изменением температуры

∂E

E = ∂T V,N T = CV,N T.

4.2Флуктуации числа частиц и объема

Систему с переменным числом частиц описывает большое каноническое распределение (для определенности выберем квантовый вариант)

68

Для дисперсии и относительной флуктуации получаем

Эти формулы более предпочтительны по сравнению с (83) и (84), т.к. для вычисления по ним нужно лишь уравнение состояния системы ( f(T, V, p, N) = 0).

Например, для идеального одноатомного газа

чем плотность может меняться либо за счет изменения числа частиц в фиксированном объеме, либо за счет изменения объема при фиксированном числе частиц:

69