Смирнов Стат Физ

Тогда

В этом приближении

Вычислим свободную энергию

F = −kT ln Z = Fèä − kT ln QN .

Nω

Будем считать, что V 1. Как увидим далее, это оправдано в достаточно разреженных газах.

Таким образом,

F = Fèä + N(N − 1)kT ω(T ) 2V

и для внутренней энергии находим

Смоделируем потенциальную энергию взаимодействия атомов следующим образом (модель слабо взаимодействующих твердых шаров диаметра d, см. рис. 4b)

30

средняя по объему энергия парного взаимодействия. Подставим это выражение для ω в уравнение состояния (44)

Уравнение состояния, справедливое в большом диапазоне давлений для газа, обычно записывают в виде

B(T ), C(T ) и т.д. носят название вириальных коэффициентов (первого, вто-

рого и т.д.). В уравнении Ван-дер-Ваальса B(T ) = b− a , C(T ) = b2. Сравнивая с полученным ранее уравнением состояния, получаем NkT

Таким образом, b имеет смысл учетверенного объема всех атомов газа, а a/V имеет смысл средней по объему энергии парного взаимодействия всех атомов (в газе из

т.е. к энергии идеального одноатомного газа добавляется энергия парного взаимодействия атомов.

3Элементы квантовой статистической физики

При квантово-механическом описании системы нельзя пользоваться классическим понятием состояния. В квантовой механике состояние описывается волновой функцией. В квантовой механике отсутствует понятие траектории движения частицы. По соотношению неопределенностей

q p ≥ ~2

31

(~ = 2hπ, где h постоянная Планка; ~ = 1.05Ч10−34 Дж·с) частица в квантовомеханических состояниях движения не может иметь одновременно вполне опреде-

ленных значений координат и импульсов. Вообще в квантово-механических состояниях система может иметь, а может и не иметь определенных значений физических величин.

Состояния с определенной энергией называются стационарными. Сама энергия системы может принимать либо дискретный, либо непрерывный набор значе- ний (это зависит от устройства самой системы, от характера взаимодействия ее частей).

Величины, которые может принимать энергия, носят название уровней энергии. Говорят, что уровень энергии системы вырожден, если имеется более одного микросостояния с данной энергией, а число независимых микросостояний с данной энергией называется кратностью вырождения уровня. Сами микросостояния с данной энергией различаются друг от друга тем, что другие физические величины принимают в них разные значения. При квантовом рассмотрении системы также можно выделить совокупность физических величин, которые являются интегралами движения (сохраняются). Они, так же как энергия, могут иметь в стационарных состояниях определенные значения.

Для примера рассмотрим линейный одномерный гармонический осциллятор частицу массы m, движущуюся под действием упругой силы. Функция

Гамильтона гармонического осциллятора

При классическом рассмотрении энергия может быть какой угодно положительной E ≥ 0. А при фиксированной энергии осциллятор при своем движении проходит че-

рез множество классических микросостояний, задаваемых значениями координат q(t) и импульсов p(t). В квантовом случае энергия осциллятора может прини-

мать только дискретный ряд значений

Каждому уровню энергии соответствует лишь одно микросостояние, т.е. уровни энергии осциллятора являются невырожденными.

Другой пример: плоский ротатор материальная точка массы m, которая может двигаться по окружности радиуса r(ее момент инерции I = mr2). Ýòî ñè-

стема с одной степенью свободы. В качестве обобщенной координаты выберем угол ϕ, определяющий положение материальной точки на окружности. Классическое

выражение для энергии плоского ротатора ( функции Гамильтона)

32

ãäå pϕ обобщенный импульс, сопряженный координате ϕ и имеющий смысл момента импульса относительно центра вращения. Классическая энергия ротатора может принимать любое неотрицательное значение. Квантовые микросостояния плоского ротатора можно нумеровать квантовым числом m, которое может при-

нимать значения m = 0, ±1, ±2, ..., а энергия в этих микросостояниях равна

т.е. все уровни энергии квантового плоского ротатора двукратно вырождены за исключением основного, самого нижнего (с m = 0).

Еще один пример: пространственный ротатор материальная точка массы m, которая может двигаться по поверхности сферы радиуса r(момент инерции относительно центра вращения тоже I = mr2). Это система с двумя степенями

свободы: положение точки на сфере можно задать двумя сферическими углами θ и ϕ. Классическое выражение для энергии пространственного ротатора ( функция Гамильтона):

В классической механике пространственный ротатор может иметь любую неотрицательную энергию. В квантовой механике пространственный ротатор имеет дискретный набор уровней

Каждый уровень 2l + 1 раз вырожден. Состояния с заданной энергией различа-

ются проекциями момента количества движения на выделенное направление (на- пример, на ось Z, Mz), которые тоже принимают дискретный набор значений

Mz = ~m, m = 0, ±1, ±2, ..., l.

Но есть пограничный случай движения, когда возможно как квантово-меха- ническое, так и классическое описание. В этом случае можно установить соответствие между объемом фазового пространства, в котором происходит классиче- ское движение и числом квантово-механических микросостояний. Оказывается, что

одному квантовому микросостоянию соответствует объем фазового пространства равный h3N (для систем с 3N степенями свободы). В этом случае интегрирование

по фазовому пространству соответствует суммирование по квантовым состояниям. Кроме того согласно квантовой механике перестановка частиц в системе тожде-

ственных частиц не означает появление нового микросостояния. Поэтому в фазо- вом пространстве N! объемчиков h3N (по числу всех перестановок в системе из

N частиц), разбросанных по фазовому пространству перестановками, соответствуют одному микросостоянию, т.е. одному микросостоянию в фазовом пространстве

33

соответствует объем h3N N!, а выделенному объему dqdp в фазовом пространстве

dqdp

соответствует d = h3N N! микросостояний. Поэтому интегрирование по фазовому

1

пространству в классической статистической физике с учетом множителя h3N N! эквивалентно суммированию по микросостояниям.

При квантовом описании микродвижений с самого начала пользуются понятием микросостояния в квантовом понимании. Для систем, занимающих конечный объем, эти микросостояния дискретны. В квантовой статистике вводят функцию распределения по микросостояниям. Мы ее будем обозначать ρ(Eα) , ãäå α ≡ (i, n)

индекс микросостояния (i нумерует уровни энергии, а n различает микросо-

стояния с заданной энергией, если энергетический уровень вырожден). Условие нормировки для функции распределения запишется в виде

ãäå gi кратность вырождения уровня энергии Ei.

Если уровни энергии располагаются очень близко друг к другу (спектр энергии почти непрерывный или непрерывный), то можно рассматривать непрерывное распределение по энергии. Условие нормировки тогда запишется в виде

Z

ρ(E)g(E)dE = 1,

где g(E)dE число микросостояний, приходящихся на интервал энергий dE.

Перейдем к формулировке квантовых аналогов рассмотренных ранее классиче- ских распределений. Ансамбли (микроканонический, канонический, большой канонический) в квантовой статистике определяются так же, как и в классической с той лишь разницей, что теперь речь идет о распределении систем ансамблей по квантовым микросостояниям, т.е. теперь для описания движений микрочастиц используются законы квантовой механики.

3.1Квантовое микроканоническое распределение

Энергия систем ансамбля фиксирована, а все микросостояния с заданной энергией

равновероятны

для случаев дискретного и непрерывного спектра энергий системы соответственно. Для макроскопических систем спектр энергий можно считать непрерывным. Число микросостояний равно W = g(E, V, N)ΔE , и по статистическому определению

энтропии (12)

S(E, V, N) = k ln g(E, V, N)ΔE.

Остальные термодинамические характеристики вычисляются так же, как в слу- чае классической статистики (см. раздел 2.11).

34

3.2Квантовое каноническое распределение

Функцию квантового канонического распределения можно вывести из квантового микроканонического совершенно так же, как в разделе 2.12:

Z называется статистической суммой (статсуммой). Все этапы вычисления тер-

модинамических характеристик в квантовой статистике такие же, как в класси- ческой, но вместо статистического интеграла нужно вычислять статистическую сумму.

3.3Квантовое большое каноническое распределение

Функция квантового большого канонического распределения выводится из квантового микроканонического распределения совершенно так же, как в классической статистике(см. раздел 2.13):

Zqgc = Zqgc(T, V, µ) называется большой статистической суммой и вычисляется из условия нормировки

Далее термодинамический потенциал и другие термодинамические характеристики системы вычисляются так же, как в случае классической статистики.

Рассмотрим некоторые модельные системы методами классической и квантовой статистик и сравним их результаты.

3.4Идеальный газ гармонических осцилляторов

а) Классическое рассмотрение.

Для системы классических невзаимодействующих одномерных осцилляторов (идеальный газ осцилляторов) функция Гамильтона записывается следующим образом

35

Статистический интеграл обычным образом выражается через интеграл по фазовому пространству одного осциллятора

Далее вычисляем внутреннюю энергию (32)

E = kT 2 ∂ ln Z = NkT ∂T

и теплоемкость

C = ∂E∂T = Nk.

Отметим, что Zo в (50) имеет вид произведения множителей, пропорциональных T 1/2 и относящихся к кинетической и потенциальной энергии осциллятора. Соот-

ветственно внутренняя энергия и теплоемкость принимают такую форму, что можно говорить о вкладе в них, связанном с кинетической и потенциальной энергией движения отдельно.

б) Квантовое рассмотрение.

Так как осцилляторы не взаимодействуют друг с другом, то микросостояние α системы в целом определяется микросостояниями отдельных осцилляторов nj (α ≡ (n1, n2, ..., nN ) ≡ [nj]) , а энергия системы равна сумме энергий отдельных

статистической сумме сводится к независимому суммированию по nj для каждо- го осциллятора. Однако при этом каждое микросостояние будет учтено N! раз, т.к.

перестановка тождественных осцилляторов (перестановка членов в последователь-

ности (n1, n2, ..., nN )) не приводит к новому микросостоянию. Поэтому результат суммирования следует разделить на N! ≈ Ne N .

36

~ω

где введена характеристическая колебательная температура To = k è áåç-

размерная температура τ = TT . Для внутренней энергии идеального газа одномерных осцилляторов получаемo

и для его теплоемкости

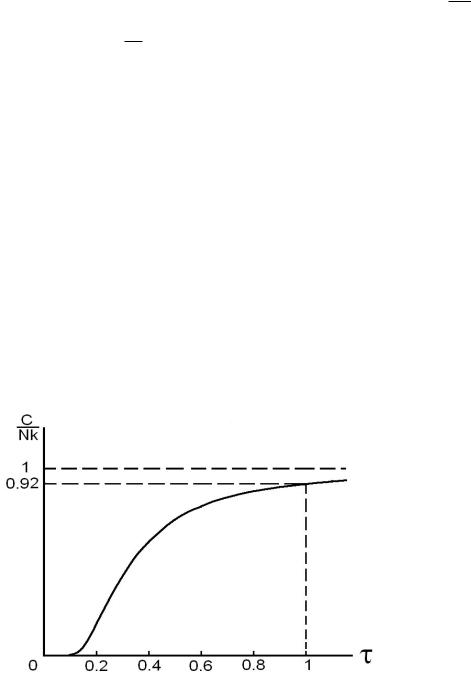
Общий ход теплоемкости (52) как функции безразмерной температуры τ приведен на рис. 5.

Ðèñ. 5: График зависимости (52) теплоемкости C от безразмерной температуры τ.

Рассмотрим предельные случаи.

а) Низкие температуры: T To èëè τ 1,

37

б) Высокие температуры: T To èëè τ 1,

Сравнение результатов классического и квантового рассмотрения наглядно показывает существенную разницу в макроскопических свойствах классической и квантовой систем. В предельном случае высоких температур результаты квантового рассмотрения переходят в результаты классического. Температура To, разде-

ляющая области низких и высоких температур, определяется в случае осциллятора его частотой. Характерные частоты колебаний атомов в молекулах ω 1013 ÷1014;

To 103K.

Например, для двухатомных газов значения температур To приведены в табли- öå 1.

Таблица 1: Температуры To для некоторых двухатомных газов

Ãàçû N2 O2 H2 HCl HBr

To K 3340 2230 5800 4140 3700

Комнатные температуры нельзя считать высокими и учет квантового характера колебаний в молекулах является необходимым при вычислениях термодинамиче- ских свойств многоатомных газов.

3.5Идеальный газ плоских ротаторов

phantom ( а) Классическое рассмотрение

Для системы невзаимодействующих ротаторов ( идеальный газ ротаторов)

функция Гамильтона (см. раздел 3 ):

внутреннюю энергию

E = kT 2 ∂ ln Z = 1NkT, ∂T 2

и теплоемкость

C = 12Nk.

38

На один ротатор приходится энергия 12kT , вклад в теплоемкость (на один ротатор)

12k не зависит от величин, характеризующих ротатор (момент инерции I). б) Квантовое рассмотрение

Квантовое микросостояние системы невзаимодействующих ротаторов определяется заданием состояний отдельных ротаторов: α ≡ (m1, m2, ..., mN ) ≡ {mj}, а энергия системы ротаторов равна сумме энергий отдельных ротаторов:

Как и в случае осцилляторов статистическая сумма системы в целом выражается через статистическую сумму одного ротатора:

Используя безразмерную температуру, можно написать в общем случае для теплоемкости идеального газа ротаторов

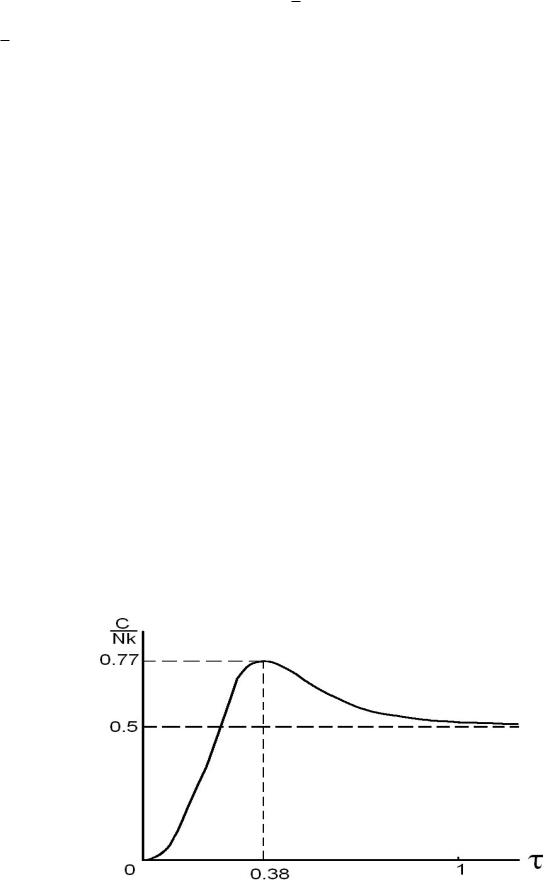
Общий ход теплоемкости (54) идеального газа плоских ротаторов как функции безразмерной температуры τ представлен на рис. 6.

Ðèñ. 6: График зависимости (54) теплоемкости C от безразмерной температуры τ.

39