_12Л_ЗаконыАЛ и Базис

Основные законы булевой алгебры

Для математических сложных выражений устанавливается определенный порядок их расчета. В алгебре логики сложные логические выражения выполняются в следующей последовательности:

1)инверсия;

2. конъюнкция;

3. дизъюнкция.

Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.

Над логическими выражениями производят тождественные преобразования с использованием законов булевой алгебры.

Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.

Две эквивалентные функции, приравненные друг к другу, называются тождеством.

1. Переместительный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

2. Сочетательный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции) при этом значение булевой переключательной функции не изменяется.

3. Распределительный закон

Распределительный закон здесь также справедлив, как и в обычной алгебре. Специфика его в булевой алгебре проявляется в некоторых частных случаях. Эти специфичные случаи и формулируются как распределительный закон булевой алгебры:

—для конъюнкции

конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;

—для дизъюнкции

(a v b)(a v c)=a v bc,

дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.

Справедливость распределительного закона для дизъюнкции докажем следующими простейшими преобразованиями:

(a v b)(a v c)= (aa v ac v ab v bc)=a v a(b v c) v bc=a(1 v (b v c)) v bc .

В результате получаем

(a v b)(a v c)=a v bc,

так как 1 v (b v c)=1 независимо от выражения в скобках.

4. Закон инверсии. Закон де Моргана.

—для дизъюнкции

отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;

—для конъюнкции

отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.

Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.

Таблица. Закон отрицания (де Моргана) для дизъюнкции

Таблица.Закон отрицания (де Моргана) для конъюнкции

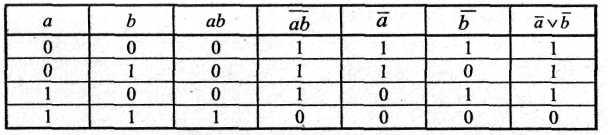
Таблицы 1.5; 1.6 показывают, что на одинаковых наборах переменных значения функций совпадает. Законы де Моргана доказаны.

5. Законы повторения

— для дизъюнкции.

—для конъюнкции

Многократное логическое сложение (логическое умножение) одной переменной равно самой этой переменной.

Законы повторения булевой алгебры существенно отличаются от законов повторения обычной алгебры.

6. Закон двойного отрицания

Двойное отрицание логической переменной равно самой логической перемененной.

7. Соотношения с нулем и единицей

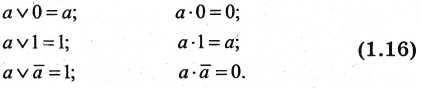
8. Закон склеивания:

Докажем законы склеивания эквивалентными преобразованиями

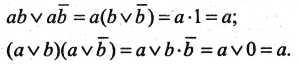
9. Законы поглощения

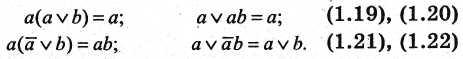
Доказательства законов поглощения

10. Умножение и сложение переменной и функции

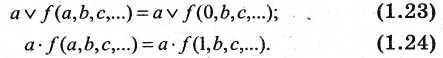
Формулы умножения и сложения позволяют существенно упростить техническую реализацию логического устройства, заменить переменную некоторой константой: логической 1 либо логическим 0.

Пример.

Правила алгебры логики позволяют преобразовать логическую функцию к виду, удобному для реализации в виде логического устройства.

Например, задана функция

Для реализации функции в данном виде требуется два инвертора НЕ, три трехвходовых элемента ЗИ, один трехвходовый элемент ЗИЛИ (рис. 1).

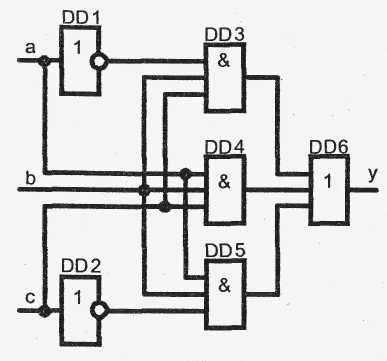
Рис. 1

Проведем эквивалентные преобразования с использованием закона поглощения

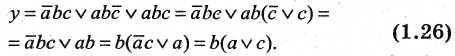
Очевидно, что после преобразования функция значительно упростилась. Для реализации теперь достаточно иметь один двухвходовый элемент 2И, один двухвходовый элемент 2ИЛИ (рис.3). Обе схемы позволяют реализовать одну и ту же функцию.

Всего же существует 4 функции одной переменной и 16 функций двух переменных. С помощью элементарных функций можно построить любую сложную логическую функцию. При рассмотрении законов булевой алгебры использовались только три элементарные функции (НЕ, И, ИЛИ). Следовательно, в наборе элементарных функций существует избыточность.

Базис

Всего существует 4 функции одной переменной и 16 функций двух переменных. Очевидно, что с помощью этих элементарных функций можно построить любую сложную логическую функцию, но оказывается фактически можно обойтись значительно меньшим набором функций.

Базисом называется функционально полная система (совокупность) логических элементов, которая позволяет реализовать любую логическую схему произвольной сложности.

Для построения сложной логической функции нет необходимости использовать все элементарные функции. Можно уменьшить набор элементарных функций, исключая из него функции, которые можно выразить через другие. Последовательно исключая из базиса функции, получают минимальный базис.

Под минимальным базисом понимают такой набор функций, исключение из которого любой функции превращает полную систему в неполную.

При рассмотрении законов булевой алгебры использовались только три элементарные функции (НЕ, И, ИЛИ). Этих логических функций достаточно чтобы выразить любую элементарную функцию и построить любое сложное логическое устройство. Следовательно, набор из трех функций (И, ИЛИ, НЕ) является базисом.

Базис (И, ИЛИ, НЕ) не является минимальным. Используя закон де Моргана из него можно исключить одну из функций И либо ИЛИ. Действительно функцию И можно реализовать через функции (НЕ, ИЛИ):

что легко доказать составив таблицы истинности для левой и правой частей уравнения.

Функцию ИЛИ тоже можно реализовать через функции (НЕ, И):

Наборы (НЕ, И) и (НЕ, ИЛИ) так же являются базисами.

Обычно логические схемы строятся на основе инвертирующих усилителей на транзисторах. Технически удобно изготавливать логические элементы совмещающие в себе сразу две функции например И-НЕ или ИЛИ-НЕ. Каждый из элементов И-НЕ (штрих Шеффера) и ИЛИ-НЕ (стрелка Пирса) в отдельности является функционально полным базисом и позволяет синтезировать любое сколь угодно сложное логическое устройство.

Рассмотрим, для примера, реализацию функций НЕ, ИЛИ, И в базисе (И-НЕ):

1. Для реализации инверсии НЕ достаточно просто подать входной сигнал на оба входа одновременно.

.

2. Для реализации дизъюнкции ИЛИ с помощью схемы И-НЕ — воспользоваться законом де Моргана, т.е. сначала инвертировать входные сигналы, а потом над результатами выполнить операцию И-НЕ.

3. Для конъюнкции — сначала применить операцию И-НЕ, а затем инвертировать входные сигналы.

Их схемное решение показано на рис. 2.

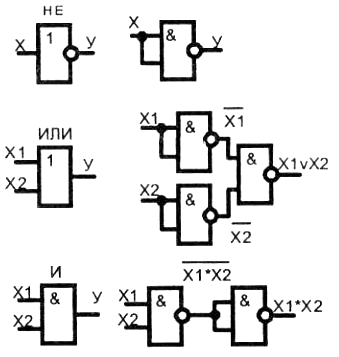
Рис. 2

Привлекательность базисов из одной логической функции (И-НЕ) либо (ИЛИ-НЕ) заключается в том, что все логическое устройство построено только на однотипных логических элементах. Получаем логическую схему, которая обладает регулярной структурой. Необходимо только осуществить коммутацию одинаковых логических элементов. Базисы на логических элементах (И-НЕ), (ИЛИ-НЕ) широко используются при проектировании больших интегральных микросхем, потому что уменьшают количество типов элементов и технологий для их реализации.

Недостатком минимальных базисов является увеличение числа логических элементов в схеме, что приводит к ее усложнению и увеличению временных задержек. Поэтому на практике часто используют неминимальные базисы. Возможны различные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для построения логических устройств обусловлен тем, насколько экономически удобно и просто выполнить элементы, технически реализующие входящие в базис функции, и все логическое устройство в целом.

Анализ комбинационных устройств (без памяти)

Комбинационные устройства — цифровые устройства, выходные сигналы которых зависят только от входных сигналов, действующих в текущий момент времени, и не зависят от предыдущего внутреннего состояния или предшествующих входных сигналов. Другими словами, комбинационные устройства — это устройства без памяти. Их можно представить в виде многомерного п, т — многополюсника (рис. 3).

Рис. 3

Условия функционирования комбинационного устройства можно представить в виде системы логических функций, называемых функциями выходов

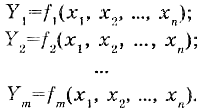
Задача анализа функционирования комбинационного сводится к определению всех функций выходов дискретного устройства по известной принципиальной схеме реального устройства. Результат анализа представляется в виде функций алгебры логики и/или таблицы истинности.

1. Порядок анализа

1. На функциональной схеме выходы всех базовых логических элементов (ЛЭ) обозначить внутренними переменными.

2. Составить по функциональной схеме логические функции для каждого базового логического элемента.

3. Путем подстановок исключить все внутренние переменные. Получить формулы зависимости выходов у₁,...у_т от его входов x₁,....х_п.

4. Составить таблицы истинности.

5. Представить результаты анализа в удобной для пользователя форме.

Последний пятый пункт алгоритма анализа в общем случае уже является переходом к задаче синтеза комбинационного устройства.

2. Пример анализа

Рассмотрим анализ приведенной на рис.4 схемы

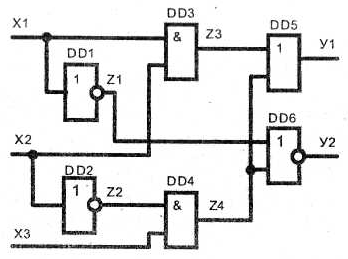
Рис.4

Обозначим промежуточные переменные через z₁, z₂, z₃, z₄ и запишем функции передачи для каждого ЛЭ.

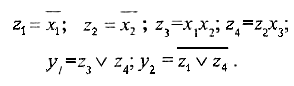
Исключим внутренние промежуточные переменные

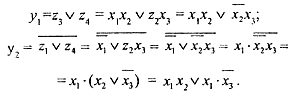
Составим таблицу истинности

Таблица истинности комбинационного устройства.

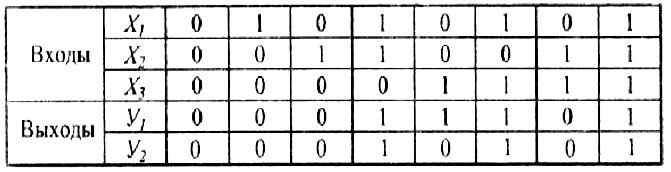
Таблицы истинности могут быть записаны в других формах, которые могут оказаться более удобными. Это могут быть карты Вейча, карты Карно и т.д.