Тема 1. Оценка погрешности вычислений

Вопросы для самоподготовки

1. Этапы решения задачи на ЭВМ

2. Абсолютная и относительная погрешности

3. Значащие цифры в записи числа

4. Правила округления чисел

5. Верные цифры. Верная цифра в строгом смысле

6. Нахождение абсолютной погрешности при простейших арифметических действиях и вычислении элементарных функций

7. Систематический учет погрешностей при вычислениях

8. Метод подсчета цифр при определении погрешностей

9. Метод границ определения погрешности

Краткая теория

Под погрешностью понимается величина, характеризующая точность результата. Различают три основных вида погрешностей.

1) Погрешность задачи – связана с приближенным характером исходной содержательной модели (в частности, с невозможностью учесть все факторы в процессе изучения моделируемого явления), а также ее математического описания, параметрами которого служат обычно приближенные числа (например, из-за принципиальной невозможности выполнения абсолютно точных измерений). Для вычислителя погрешность задачи следует считать неустранимой (безусловной), хотя постановщик задачи иногда может ее изменить.

2) Погрешность метода – связанна со способом решения поставленной математической задачи и появляющаяся в результате подмены исходной математической модели другой или конечной последовательностью других, например, линейных моделей. При создании численных методов закладывается возможность отслеживания таких погрешностей и доведения их до сколь угодно малого уровня. Отсюда естественно отношение к погрешности метода как к устранимой (или условной).

3) Погрешность действий обусловлена необходимостью выполнять арифметические операции над числами, усеченными до количества разрядов, зависящего от применяемой вычислительной техники (если, разумеется, не используются специальные программные средства, реализующие, например, арифметику рациональных чисел).

Эти погрешности в сумме дают полную погрешность результата решения задачи. Первый тип погрешности служит ориентиром точности, с которой следует рассчитывать математическую модель. Нет смысла решать задачу существенно точнее, чем это диктуется неопределимостью исходных данных, т.е. погрешность метода подчиняют погрешности задачи. Так как при выводе оценок погрешностей численных методов обычно исходят из предположения, что все операции над числами выполняются точно, то погрешность округлений не должна существенно отражаться на результатах реализации методов, т.е. должна подчиняться погрешности метода. Влияние погрешностей округлений не следует упускать из вида ни на стадии отбора и алгоритмизации численных методов, ни при выборе вычислительных и программных средств, ни при выполнении отдельных действий и вычислении значений функций.

Вычислительная погрешность

Рассмотрим процесс округления чисел, записанных в десятичной системе. Оно производится по правилу первой отбрасываемой цифры:

• если первая из отбрасываемых цифр меньше 5, то оставляемые десятичные знаки сохраняются без изменения;

• если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на единицу;

• если первая из отбрасываемых цифр равна 5, а за ней идут не нули, то последняя оставляемая цифра увеличивается на единицу;

• если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней, – нули, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остаётся без изменения, если – чётная.

Это правило округления обеспечивает увеличение абсолютной погрешности не более, чем на половину последнего сохраняемого разряда.

При округлении целого числа отброшенные знаки не следует заменять нулями, надо применять умножение на соответствующие степени 10. Например: если число c = 250331 надо округлить до пяти десятичных знаков после запятой, то имеем c* = 2.5 10⁵.

В основе процессов округления лежит идея минимальности разности числа и его округлённого значения.

Поведение вычислительной погрешности зависит от правила округлений и алгоритма численного решения задачи.

Неустранимая погрешность

Неустранимая погрешность – это погрешность, связанная с ошибками в исходной информации. Причинами этих ошибок может быть, например, неточность измерений, невозможность представления данной величины конечной дробью. Обычно различают абсолютную и относительную формы ошибок.

Погрешность чисел

Значащая цифра приближённого числа в десятичной записи – это любая его цифра, в том числе и нуль, если он стоит между отличными от нуля цифрами или после них как представитель сохраняемых разрядов числа.

Если известно, что c = 3200 (т.е. точное число), то для него нельзя использовать запись c=3.2 10³, ибо тем самым два нуля переводятся в разряд незначащих цифр.

Пусть X – точное значение величины, а X^* – её приближённое значение.

Абсолютной погрешностью числа X^* называется величина DX^*, удовлетворяющая условию ½X-X^*½ £ DX^*. Относительной погрешностью называется некоторая величина dX^*, удовлетворяющая условию

.

Абсолютные и относительные погрешности числа принято округлять только в большую сторону, так как при округлениях границы неопределённости числа, как правило, увеличиваются. По этой причине вычисления ведут с одним-двумя запасными десятичными знаками.

Значащая цифра приближённого числа в десятичной записи – это любая его цифра, в том числе и нуль, если он стоит между отличными от нуля цифрами или после них как представитель сохраняемых разрядов числа.

Значащая цифра называется верной, если абсолютная погрешность числа не превосходит 1/2 единицы разряда, соответствующего этой цифре.

Погрешность значения функции

Пусть имеется функция f(x₁, x₂, …, x_n). Известны приближённые значения x₁^*, x₂^*, …, x_n^* аргументов и соответствующие им абсолютные погрешности Dx₁, Dx₂, …, Dx_n. Нужно определить неустранимую погрешность вычисления значения функции в точке (x₁, x₂, …, x_n).

Допустим, что

1) f(x₁, x₂, …, x_n) непрерывно дифференцируема в рассматриваемой области;

2) погрешности Dx₁, Dx₂, …, Dx_n. значительно меньше самих значений ½x₁^*½, ½x₂^*½, …, ½x_n^*½.

Используя непрерывную дифференцируемость функции f и учитывая, что разность между x_i^* и x_i по предположению мала, получим

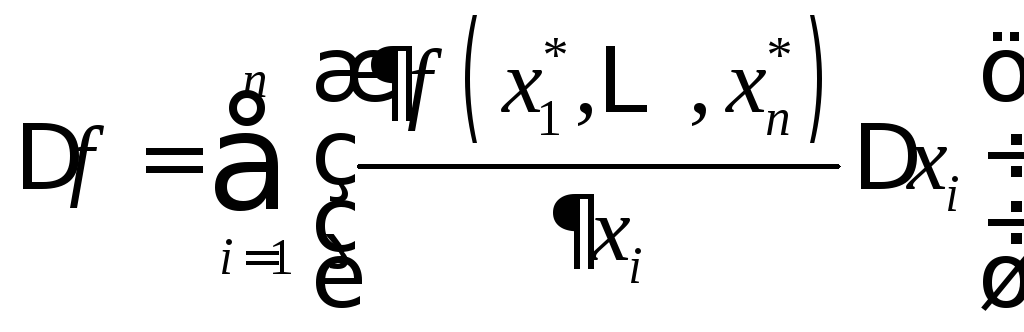. (1.1)

Соотношение (1.1) называют линейной оценкой погрешности значения функции f в точке (x₁, x₂, …, x_n). Из (1.1) следует, что относительная погрешность значения f в точке (x₁, x₂, …, x_n) равна:

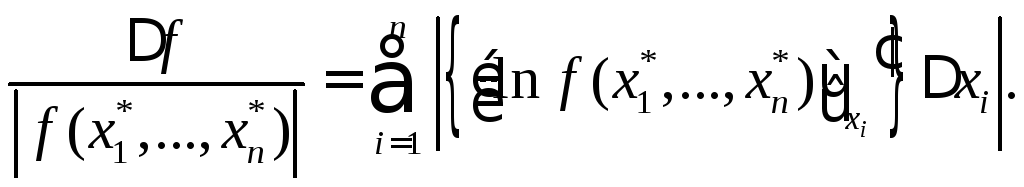
Чтобы выразить относительную погрешность f через относительные погрешности аргументов, перепишем полученное выражение в виде:

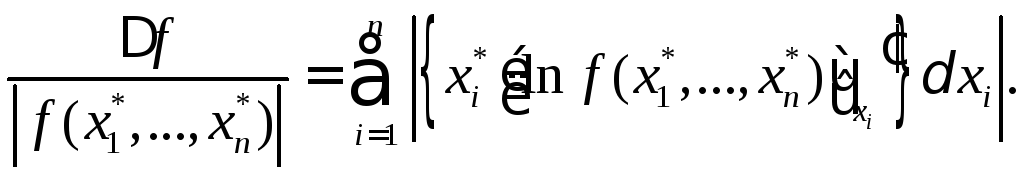(1.2)

Погрешность результатов арифметических операций

Произведём конкретные оценки в случае простейших функций: найдём абсолютные погрешности суммы , разности , произведения и частного, считая известными абсолютные погрешностии .

а) Если f(x,y) = x+y, то ;

;

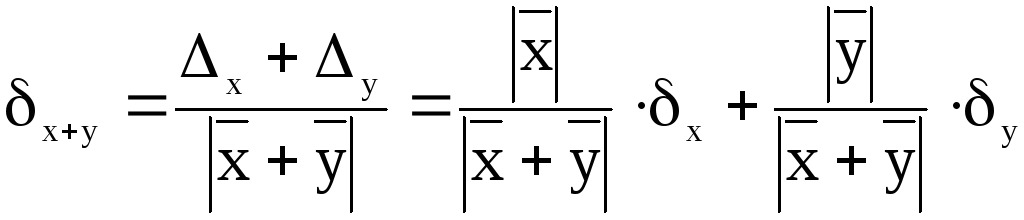б) если f(x,y) = x-y, то ;

;

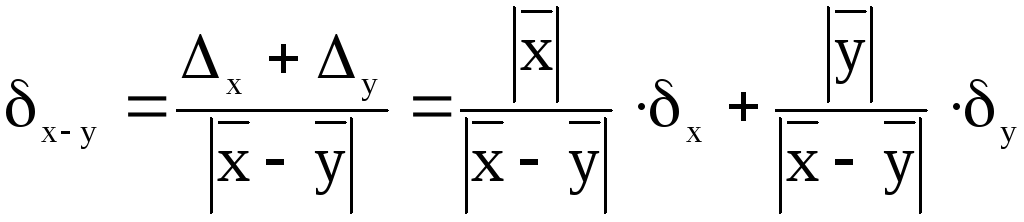в) если f(x,y) = x*y, то ;

;

г) если f(x,y) = x/y, то ;

.

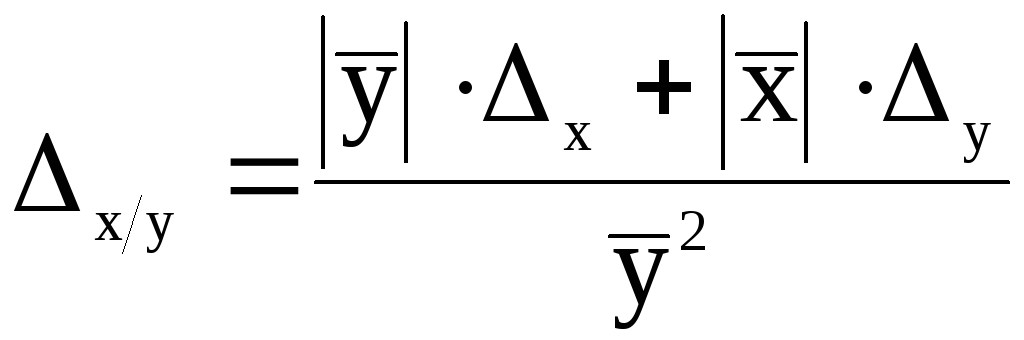Наиболее распространённым видом вычислений является вычисление по готовой формуле. Чаще всего вычислитель анализирует результат в конце счёта. Если же условия задачи заставляют вести кооперационный учёт движения погрешности, то используется один из трёх способов приближённых вычислений:

• Правила подсчёта цифр;

• Систематический учёт погрешностей;

• Метод границ.

Правила подсчёта цифр

При вычислении этим методом составляется обычная расчётная таблица, явный учёт погрешностей не ведётся, округления результатов промежуточных действий проводятся по следующим правилам:

• При сложении и вычитании приближённых чисел следует округлить число с меньшей абсолютной погрешностью (для десятичных дробей с большим количеством знаков после запятой) так, чтобы в нём осталось на один-два разряда больше, чем в точном числе. В результате считать верными столько десятичных знаков после запятой, сколько их в приближённом данном с наименьшим числом десятичных знаков после запятой;

• При умножении и делении двух приближённых чисел нужно округлить число с большим количеством значащих цифр так, чтобы в нём было лишь на одну значащую цифру больше, чем в другом числе. В результате считать верными столько значащих цифр, сколько их в приближённом данном с наименьшим числом значащих цифр;

• В значениях элементарных функций от приближённых значений аргумента (включая возведение в степень, извлечение и т.д.) в результате можно считать верными столько значащих цифр, сколько верных значащих цифр имеет значение аргумента;

• При записи промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила 1-3. В окончательном результате эта запасная цифра округляется.

Систематический учёт погрешностей

Метод предусматривает поэтапный подсчёт границ погрешностей всех промежуточных и окончательного результатов по правилам вычисления погрешностей, рассмотренных выше. Промежуточные результаты, также как и их погрешности, заносятся в специальную расчётную таблицу, состоящую из двух параллельно заполняемых частей – для результатов и их погрешностей.

Метод границ

В случае, когда не столь важно получить наиболее близкое к точному значению вычисляемой величины, сколь важно иметь абсолютно-гарантированные границы её возможных значений применяют метод границ, суть которого в следующем. Для функции u=f(x,y) из аргументов x и y необходимо вычислить f(a,b), где a и b – приближённые значения аргументов, причём совершенно точно известно, что НГ_a<a<ВГ_a, НГ_b<b<ВГ_b, где НГ и ВГ – соответственно обозначения нижней и верхней границы значений, и тогда

f(НГ_a, НГ_b) < f(a,b) < f(ВГ_a, ВГ_b),

если f возрастает по a и b, и

f(НГ_a, ВГ_b) < f(a,b) < f(ВГ_a, НГ_b),

если f возрастает по a и убывает по b.

В частности, для положительных аргументов

f(a,b) = a+b, то НГ_a + НГ_b < a+b < ВГ_a + ВГ_b;

f(a,b) = a-b, то НГ_a - ВГ_b < a-b < ВГ_a - НГ_b;

f(a,b) = a*b, то НГ_a * НГ_b < a*b < ВГ_a * ВГ_b;

f(a,b) = a/b, то НГ_a /ВГ_b < a/b < ВГ_a /НГ_b.

Расчётная граница метода имеет две строки для вычисления НГ и ВГ выражения.