Perelik_pitan

Перелік питань

1. Основні поняття теорії множин: множини, підмножини, операції над множинами, способи задання множин.

По Кантору: множина – довільна сукупність певних об’єктів нашої інтуіції або інтелекту, які можна відрізнити один ві одного і які представлені як єдине ціле.

Множиною називається об’єднання, єдине ціле визначених, відмінних один від одного однотипних об'єктів, які називаються елементами множини.

Якщо кожен елемент множини А є елементом іншої множини В, то кажуть, що А є підможиною В.

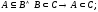
Операції: Доповнення , об’єднання , перетин , різниця \, симетрична різниця ÷

Множини задаються переліком усіх елементів, функцією, яка виконується для усіх елементів, мовою предикатів. Інакше кажучи, необхідно вказати властивість, яка виконується для всіх елементів.

2. Поняття самодвоїстої функції.

Функція f1 називається двоїстою функції f2, якщо f1(x1,x2,…,xn) =

Якщо функція двоїста сама собі, вона є самодвоїстою

3. Алгебра висловлювань. Основні закони. Формули алгебри висловлювань. Семантика числення висловлювань.

Висловлюванням називають пропозицію, до якої можна застосувати поняття істиності або хибності.

Запереченням називають висловлювання , яке істинне тоді і тільки тоді, коли висловлювання Р – хибне.

Кон’юнкцією називають висловлюваня, яке істине тоді і тільки тоді, коли P i Q істинні.

Диз’юнкцією називають висловлюваня, яке хибне тоді і тільки тоді, коли P i Q хибні.

Імплікацією Р → Q називають висловлювання типу «якщо Р, то Q». Хибне тоді и тільки тоді, коли Р істинне, а Q хибне.

Еквівалентністю P ~ Q називають висловлювання типу «Р тоді і тільки тоді, коли Q». Істинне тоді і тільки тоді, коли істинності P i Q однакові.

A˄B~B˄A A˄A~A A˅B~B˅A A˅A~A

A˅(B˄C)~(A˅B)˄(A˅C) A˄(B˅C)~(A˄B)˅(A˄C)

A˄(B˄C)~(A˄B)˄C A˅(B˅C)~(A˅B)˅C

A˅(A˄B)~A A˄(A˅B)~A

¬¬A~A ¬(A˄B)~(¬A)˅(¬B) ¬(A˅B)~(¬A)˅(¬B)

A~(A˄B)˅(A˄(¬B)) A~(A˅B)˄(A˄(¬B))

Просте висловлювання - це висловлювання, яке не можна подати як сполучення певних більш коротких висловлювань.

Складені (непрості) висловлювання будуються з простих за допомогою різних сполучників "або", "та", "отже" та інших.

4. Орієнтовані та неорієнтовані дерева.

Дерево – зв’язний граф без циклів.

Дерево – граф, у якому між двома його вершинами є тільки один шлях.

Орієнтоване дерево – вільний від петель орієнтований граф, співвіднесений граф якого є деревом.

Вершини степені 1 називаються листами, інші – внутрішніми. Вершина в самій верхній частині дерева називається коренем. Якщо корінь визначений, дерево називається кореневим.

Рівень вершини v – це довжина шляху з кореня до даної вершини. Висота дерева – довжина найдовшого шляху від кореня до листа.

Якщо найбільша зі степенів виходу вершин дерева дорівнює m, то дерево називають m-арним деревом. Коли m = 2, дерево називається бінарним деревом. У бінарному дереві кожен син батька позначається або як лівий син, або як правий син.

5. Властивості функцій алгебри логіки. Реалізація булевих функцій формулами. Рівносильні формули.

Комутативність: x1˄x2=x2˄x1 x1˅x2=x2˅x1

Асоціативність: x1˄(x2˄x3)=(x1˄x2)˄x3 x1˅(x2˅x3)=(x1˅x2)˅x3

Дистрибутивність: x1˅(x2˄x3)=(x1˅x2)˄(x1˅x3) x1˄(x2˅x3)=(x1˄x2)˅(x1˄x3)

Відповідь у 37.

Дві формули A і B називаються рівносильними, якщо їм відповідає та сама таблиця істинності. Тобто дві формули представляють одну й ту саму функцію. Інша назва – тафтологія.

6. Графи: основні поняття й операції. Метрика графа. Цикломатика графів.

Якщо задати скінченну множину V точок і скінченний набір ліній (ребер) E, що сполучають деякі пари точок з множини V, то отримана сукупність точок і ліній називатиметься графом G = (V, E). При цьому елементи множини V називаються вершинами графа, а елементи множини E - ребрами.

Якщо вершина v є кінцем ребра , то кажуть, що v і інцидентні.

У множині V можуть зустрічатися однакові елементи, ребра, що сполучають однакові елементи називаються петлями. Однакові пари у множині E називаються кратними (чи паралельними) ребрами. Кількість однакових пар (v, w) в E називається кратністю ребра (v, w).

Множина V і набір ребер E визначають граф з кратними ребрами - псевдограф.

Псевдограф без петель називається мультиграфом.

Якщо в наборі E жодна пара не зустрічається більше одного разу, то мультиграф називається графом.

Вершини v, w графа G = (V, E) називаються суміжними, якщо {v,w}Е. Два ребра називаються суміжними, якщо вони мають загальну вершину.

Степенем вершини графа називається число ребер, яким ця вершина належить. Вершина називається висячою, якщо її міра дорівнює одиниці і ізольованою, якщо її міра дорівнює нулю.

Маршрутом (шляхом) для графа G(V, Е) називається послідовність v₁e₁v₂e₂v₃…e_kv_k+1. Маршрут називається замкнутим, якщо його початкова і кінцева точки співпадають. Число ребер (дуг) маршруту (шляхи) графа називається довжиною маршруту (шляхом).

Незамкнутий маршрут (шлях) називається ланцюгом. Ланцюг, в якому всі вершини попарно різні, називається простим ланцюгом.

Замкнутий маршрут (шлях) називається циклічним маршрутом або циклом (контуром). Цикл, в якому усі вершини попарно різні, називається простим циклом.

Мінімальна довжина простого ланцюга з початком у вершині і кінцем у вершині називається відстанню між цими вершинами. Позначається: .

Ексцентриситетом вершини v називають найбільшу відстань до будь-якої вершини графа.

Діаметром кінцевого графа називається найбільша з відстаней між парою його вершин : . Або ж діаметр дорівнює найбільшому з ексцентриситетів

Вершина називається центром графа , якщо максимальне віддалення від неї до інших вершин графа набуває мінімального значення: .

Найкоротший з ексцентриситетів називається радіусом графа.

Орієнтований граф (орграф) G(V, Е), складається із множини V вершин і множини Е впорядкованих пар елементів з V, названого множиною орієнтованих ребер або просто ребер, якщо зрозуміло, що граф орієнтований. Елемент множини Е називається орієнтованим ребром. Якщо (а, b)  E, то а називається початковою вершиною ребра (а, b), a b називається кінцевою вершиною.

Якщо (a, b) - ребро орієнтованого графа G(V, E) таке, що a - початкова, а b - кінцева вершини ребра (а, b), тоді вершини а і b інцидентні до ребра (а, b). Вершина а називається суміжною до вершини b. Вершина b називається суміжною від вершини а.

Степенем виходу вершини v називається кількість ребер, для яких v є початковою вершиною, позначається outdeg(v). Степенем входу вершини v називається кількість ребер, для яких v є кінцевою вершиною, позначається indeg(v).

Якщо indeg(v) = 0, то вершина v називається джерелом. Якщо outdeg(v) = 0, то вершина v називається стоком

Цикломатика?????

7. Декартів добуток множин. Властивості. Проекції.

Декартовим добутком множин та називається множина .

Першою (другою) проекцією бінарного відношення називається множина

.

8. Поєднання (сполучення). Біном Ньютона.

Комбінація (сполучення) це кількість різних невпорядкованих вибірок без повторень об’єму k з n-елементної множини .

Комбінація з повторенням це кількість різних невпорядкованих вибірок з повтореннями об’єму k з n-елементної множини .

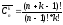9. Відповідності. Теорема Кантора.

Відповіді у питанні 38.

10. Комбінаторика (розміщення, перестановки).

Будь-який вектор довжини k, складений з елементів n-елементної множини Х, в якій усі елементи різні, називають розміщенням без повторень з n елементів по k елементів, тоді 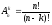. Елементи в розміщенні не поторюються.

Будь-який вектор довжини k, складений з елементів n-елементної множини Х, в якій усі елементи різні, називають розміщенням з повторенням з n елементів по k елементів, тоді . Елементи в розміщенні не поторюються.

Розміщення це кількість різних упорядкованих вибірок без повторень об’єму k з n-елементної множини.

Перестановка це кількість способів упорядкування n-елементної множини, тобто кількість різних упорядкованих вибірок об’єму n з n-елементної множини P_n = n!

Нехай 1-й елемент повторюється разів, 2-й елемент - разів і так далі. Тоді вектори довжини , складені з елементів даної множини називаються перестановками з елементів с повторами. Число таких перестановок позначається и дорівнює .

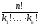Комбінація з повторенням це кількість різних невпорядкованих вибірок з повтореннями об’єму k з n-елементної множини .

11.Відображення і функції. Відображення в себе.

Функцією називається будь-яке функціональне відношення між двома множинами. Кожному елементу а (аргументу) з області визначення функція ставить у відповідсність єдиний елемент b (значення) з області значень.

Функція (відображення) — це правило, яке кожному елементу з першої множини (області визначення) ставить у відповідність один і тільки один елемент з другої множини.

Тотожне відображення (відображення в себе) — таке відображення, яке переводить кожний елемент множини (області) визначення в себе. Область визначення та область значень тотожного відображення збігаються.

12. Правило суми і правило добутку. Приклади.

Об’єкт а можна вибрати р способами, об’єкт b можна вибрати незалежно від а іншими q способами, тоді вибір а або b можна вибрати p+q способами.

Об’єкт а можна вибрати р способами, об’єкт b можна вибрати незалежно від а іншими q способами, тоді вибір а і b можна вибрати p*q способами.

13. Відношення та їх властивості. Бінарні відношення.

Відношенням R між множинами A1,A2,…An називають підмножину декартового добутку цих множин

Відповідь у 35.

Бінарне відношення – відношення між двома множинами.

14. Мова логіки предикатів (квантори, предикати).

Предикатом називається функція , де це множина деякої предметної області, а множина .

Квантор - логічний оператор, що перетворює всякий предикат на предикат меншої місності, зв’язуючи деякі змінні початкового предиката. Повсюдно вживаються два квантори: універсальний (позначається ) та екзистенціальний (позначається ).

.

.

,

.

15. Відношення еквівалентності, порядку.

Відповідь у 39 та 41.

16. Повні системи функцій. Теорема Поста про фукціональну повноту.

Система функцій ∑ називається функціонально повною, якщо будь-яка логічна функція може бути представлена суперпозицією констант і функцій з системи ∑.

Для того щоб система функцій ∑ була функціонально повною у сильному сенсі необхідно і достатньо, щоб вона містила нелінійну функцію, немонотонну функцію, функцію, що не є самодвоїстою, функцію, що не містить 0 чи 1.

17. Алгебра Жегалкіна та її основні закони. Поліном Жегалкіна.

Поліном Жегалкіна — довільна формула алгебри Жегалкіна, яка має вигляд суми по модулю 2 кон'юнкцій булевих змінних.

18 Теорема про функціональну повноту у слабкому сенсі.

Для того, що система функцій ∑ була функціонально повною в слабкому сенсі необхідно і достатньо, щоб вона містила хоча б одну немонотонну функцію і хоча б одну нелінійну функцію.

19. ДНФ. Інтервали. Покриття.

Відповідь у 25.

- множина всіх одиничних наборів функції . Тоді набір (вектор) з множини належить тоді і тільки тоді, коли . Множна називається одиничною множиною функції , а функція називається характеристичною функцією множини .

Якщо функція представлена елементарною кон’юнкцією всіх змінних, то множина містить рівно один елемент множини . Якщо функція – елементарна кон’юнкція змінних , то містить двійкових наборів. Це пояснюється тим, що в такому випадку змінних, що входять в цю кон’юнкцію несуттєві для функції . Тоді вони приймають значень, не змінюючи значення . Множина такої функції називається інтервалом.

Якщо знайти всі одиничні набори, при якій f = 1, то інтервал, що буде складатися за даних наборів, буде покривати множину та всі її підмножини.

20. Замкнуті класи. Монтонні (немонотонні) функції. Лінійні (нелінійні) функції.

Множина М логічних функцій називається замкнутим класом, якщо будь-яка суперпозиція функцій з множини М знову належить М.

Функція називається монотонною, якщо для будь-яких двох двійкових наборів довжини n з того, що a ≤ b (a ≥ b) слідує, що f(a) ≤ f(b) (f(a) ≥ f(b)). Якщо умова монотонності не виконується, то функція немонотонна.

Функція f(x₁,…,x_n) називається лінійною, якщо існують a₀,a₁,…,a_n є B такі, що f(x₁,…,x_n)=a₀+a₁x₁+…+a_nx_n. Якщо умова лінійності не виконується, то функція нелінійна.

21. Основні закони булевої алгебри.

1) Асоціативність:

2) Комутативність:

3) Дистрибутивність:

4) Ідемпотентність:

5) Подвійне заперечення:

6) Властивості констант:

7) Правила Де Моргана:

8) Закон протиріччя:

9) Закон виключення третього:

22. Еквівалентні перетворення.

Перетворення, що використовують еквівалентні співвідношення та правила заміни, називають еквівалентними.

а) Поглинання: .

б) Склеювання: .

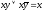в) Узагальнене склеювання: .

г) .

23. Поняття логічної функції. Таблиці істинності. Нульарні, унарні, бінарні, тернарні функції.

Логічною або булевою функцією f(x1,x2…xn) називають довільну n-місну функцію, аргументи і значення якої належать множині {0;1}.

Булева функція задається кінцевим набором значень, що дозволяє представити її у вигляді таблиці істинності.

Нульарна: При n=0 кількість булевих функцій зводиться до двох =2¹=2, перша з них тотожно дорівнює 0, а друга 1. Їх називають булевими константами — тотожний нуль і тотожна одиниця.

Унарна: Булева функція від 1 змінної.

Бінарна: Булева функція від 2-х змінних

Тернарна: Булева функція від 3-х змінних.

24. Поняття несуттєвої змінної.

Несуттєвою змінною називають змінну, яка не входить у булеву функцію.

Змінна х_і у функції f(x₁…x_i…x_n) називається фіктивною (несуттєвою), якщо f(x₁…x_і-1,0,х_і+1…x_n)= f(x₁…x_і-1,1,х_і+1…x_n) при будь-яких інших змінних.

25. Булева алгебра. ДНФ. ДДНФ. ДКНФ.

Булевою алгеброю логічних функцій називають алгебру виду 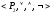, базовою множиною якої є множина логічних функцій, а операціями – диз’юнкція, кон’юнкція та заперечення.

Диз’юнктивна нормальна форма (ДНФ) – формула, яка має виглад диз’юнкції елементарних кон’юнкцій.

Кон’юнктивна нормальна форма (КНФ) – формула, яка має виглад кон’юнкції елементарних диз’юнкцій.

Досконала диз’юнктивна нормальна форма (ДДНФ) – формула, яка має виглад диз’юнкції елементарних кон’юнкцій (елементарні кон’юнкції містять всі елементи).

Досконала кон’юнктивна нормальна форма (ДКНФ) – формула, яка має виглад кон’юнкції елементарних диз’юнкцій (елементарні диз’юнкції містять всі елементи).

26. Основні поняття та способи задання булевих функцій. Булеві функції однієї (двох) змінних.

Дивитись питання 23

Булева функція задається у вигляді таблиці, або графіка зі стандартним (лексикографічним) розташуванням наборів аргументів, або формулами, що містять змінні та операції диз’юнкції, кон’юнкції та заперечення

Відповідь у 23.

27. Поля і кільця. Приклади.

Впорядкована трійка (K,+,⋅), де K ≠ Ø, називається кільцем, якщо виконуються умови:

1. (K,+) – абелева група;

2. (К, ⋅) – півгрупа;

3. Операція «⋅» дистрибутивна зліва і справа відносно операції «+» на К, тобто для ∀ a,b,c ∈ K справедливо a⋅(b+c)=ab+ac i (b+c) ⋅a = ba+ca

Кільце (K,+,⋅) називається кільцем з одиницею, якщо в K існує одиничний елемент e, відмінний від нульового. Якщо операція множення комутативна, то таке кільце називають комутативним.

Впорядкована трійка (Р, +, ∙), де P – множина, що містить не менше двох елементів, називається полем, якщо виконуються умови:

1. (Р, +, ∙) – комутативне кільце з одиницею;

2. для кожного елемента a ϵ Р, a ≠ 0, існує в Р обернений до нього елемент а^-1, тобто такий, що а∙а^-1=а^-1∙а=1

3. Для кожного ненульового елемента а і будь-якого елемента b існує єдиний елемент х, такий що ах = b.

Приклад поля: ( Q, +, ∙)

Комутативне кільце: ( Z, +, ∙)

28. Суперпозиція. Замкнуті класи функцій. Тотожність функцій.

Суперпозицією кількох функцій називають нову функцію, яка отримана за допомогою підстановок даних функцій одна в одну та перейменуванням змінних.

Відповідь в 20.

Дві функції, які при будь-яких значеннях змінної приймають однакові значення, називають тотожно рівними.

29. Доведення у логіці предикатів (метод інтерпретацій).

Метод доказу формул, що містять змінні, шляхом безпосередньої підстановки в них констант називається методом інтерпретацій або методом моделей. Підстановка констант дозволяє інтерпретувати формулу як осмислене твердження про елементи конкретної множини. Тому такий метод, що з’ясовує істинність формули шляхом звернення до її можливого сенсу називається семантичним (смисловим). Метод інтерпретацій зручний для доведення здійснимості формул або їх нееквівалентності, оскільки і в тому, і в іншому випадку досить знайти одну відповідну підстановку. Він зручний також для дослідження істинності формул на скінченних областях. Річ у тому, що якщо область скінченна, то квантори переходять в скінченні формули логіки виразів :

, .

Замінюючи всі квантори по цих співвідношеннях, будь-яку формулу логіки предикатів можна перевести у формулу, що складається з предикатів, сполучених логічними операціями. Істинність такої формули на скінченній області перевірятимуться скінченним числом підстановок і обчислень. Методи міркувань, які використовують тільки скінченні множини скінченних об'єктів називаються фінітними.

Для нескінченних областей, в загальному випадку, при доведенні тотожної істинності формул метод інтерпретації пов'язаний з великими труднощами. Тому для побудови множини істинних формул в логіці предикатів вибирається інший шлях. Ця множина породжується з деяких початкових формул (аксіом) за допомогою формальних процедур - правил виводу. Використовуються лише формальні, зовнішні властивості послідовності символів, що утворюють формули, причому ці властивості повністю описуються правилами виводу. Множини, породжені таким формальним методом, називаються формальними.

30. Поняття алгебраїчної системи на прикладі решітки.

Визначення у 33.

Решітка – алгебра, несуча множина якої частково упорядкована відношенням нестрого порядку, з двома бінарними операціями , причому виконується ідемпотентність, комутативність, асоціативність та поглинання.

31. Гомоморфізм. Ізоморфізм. Мономофізм. Епіморфізм.

A=<M,>

B=<Q,>

Гомоморфізмом алгебри А в В назифають функцію f такого виду, що перетворює множину М в Q так, що виконується умова: а є М,

Бієктивний гомоморфізм називається ізоморфізмом.

Ін’єктивний гомоморфізм називається мономорфізмом.

Сюр’єктивний гомоморфізм називається епіморфізмом.

32. Поняття замикання множини.

Множина є замкнутою відносно деякої операції, якщо результатом виконання цієї операції над елементами множини завжди буде елемент цієї множини.

33. Поняття алгебраїчної системи на прикладі групи і півгрупи.

Нехай дано деяку множину М, на якій задано сукупність операцій (сигнатура), тоді стуктура виду називають алгеброю, причому М називається несучою множиною.

Напівгрупа – алгебра, яка містить одну асоціативну бінарну операцію. Напівгрупа, що містить нейтральний елемент (одиницю), називається моноїд.

Група – моноїд, у якому для будь-якого елемента існує оберенений елемент.

34. Поняття потужності множини.

Потужністю множини називають кількість елементів даної множин.

35. Властивості відношень.

Відношення R називається рефлексивним, якщо для будь-якого елемента а є А → aRa.

Відношення R називається антирефлексивним, якщо ні для якого елемента а є А не виконується aRa.

Відношення R називається симетричним, якщо для будь-яких (а,b) є АxA: aRb → bRa.

Відношення R називається антисиметричним, якщо для будь-яких (а,b) є АxA: aRb bRa → a = b.

Відношення R називається транзитивним, якщо для будь-яких елементів а, b, c: aRb bRc → aRc.

36. Теорія графів. Основні визначення. Способи задання графів.

Відповіді у 6.

Малюнок, матриця інцидентності (ребра та вершини), матриця суміжності (вершини)

37. Подання булевих функцій: диз’юнктивна нормальна форма, кон’юктивна нормальна форма, алгебраїчна нормальна форма або поліном Жегалкіна.

Будь-яку логічну функцію можна подати у вигляді ДНФ, КНФ або у вигляді поліному Жегалкіна.

Визначення у 25 та 17.

38. Відповідність між множинами : графіки, область визначень і значень, образ, прообраз, обернена відповідність, композиція відповідностей.

Відповідністю між множинами A і B називають деяку множину G, яка є підмножиною декартового добутку А х B.

Якщо пара (a,b) є G, то говорять, що b відповідає а привідповідності G. При цьому множину всіх елементів а називають областю визначення D(G), а множину відповідних елементів b – областю значень E(G).

Кожен елемент b є B, що відповідає конкретному елементу а є А називається образом а при відповідності G. Елемент а у свою чергу називається прообразом b при відповідності G.

Нехай . Якщо відповідність Н така, що пара (b,a) є Н тоді і тільки тоді, коли (a,b) є G, то Н називають оберененою до G.