1. _{Проблема надежности и ее значение для современной техники. Основные задачи надежности ЭЭС.}

Теория надежности служит научной основой деятельности лабораторий, отделов, бюро и групп надежности на предприятиях, в проектных, научно-исследовательских и эксплуатационных организациях. Математический аппарат теории надежности основан на таких разделах современной математики, как теория вероятностей и математическая статистика, теория случайных процессов, теория массового обслуживания, математическая логика, теория графов, теория оптимизации, теория экспертных оценок, теория больших систем.

С проблемой надежности в электроэнергетике связаны следующие практические задачи [1]:

- статистическая оценка и анализ надежности действующего оборудования и установок;

- прогнозирование надежности оборудования и установок;

- нормирование уровня надежности;

- испытания на надежность;

- расчет и анализ надежности;

- оптимизация технических решений по обеспечению надежности при проектировании, создании и эксплуатации электротехнического оборудования, установок, систем;

- экономическая оценка надежности.

Теория надежности вводит в практику инженерного исследования количественные оценки, которые позволяют:

- устанавливать требования и нормативы надежности оборудования для установок и систем;

- сравнивать различные виды оборудования, установок и систем по их надежности;

- рассчитывать надежность установок по надежности их элементов;

- оптимизировать величину необходимого резерва и структуру технических объектов;

- выявлять наименее надежные элементы оборудования, установок и систем;

- оценивать сроки службы оборудования и установок.

Проблема анализа и расчета надежности систем электроснабжения (СЭС) и электроэнергетических систем (ЭЭС) связана с решением ряда теоретических и практических задач. Для этого необходимо:

- выбрать меру надёжности;

- дать математическое описание явлений, связанных с ненадежной работой оборудования и всей установки или системы в целом;

- разработать математическую модель взаимосвязи отдельных явлений, определяющих возникновение повреждений и нарушений работы установки и ее восстановление, как случайный процесс;

- дать предложения по учету надежности в моделях принятия технических решений в проектных и эксплуатационных задачах.

Основные результаты, получаемые в процессе анализа и решения задач надежности электроснабжения, используются в таких дисциплинах, как «Электрическая часть станций и подстанций», «Переходные процессы в электроэнергетических системах», «Экономика энергетики», «Релейная защита», «АСУ и оптимизация режимов энергосистем», «Организация и управление предприятиями энергетики», и ряде других специальных дисциплин.

2. Основные термины и определения надежности ЭЭС.

Надежность – свойство объекта сохранять во времени в установленных пределах значение всех параметров, установленных нормативно-технической документацией, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования [4].

Надёжность технической системы является сложным свойством, которое в зависимости от назначения объекта и условий его применения состоит из сочетаний свойств: безотказности, долговечности, ремонтопригодности, сохраняемости, живучести и т.д.

Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки.

Долговечность – свойство объекта непрерывно сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.

Кроме того, все ЭЭС и её составные части делятся на ремонтируемые и неремонтируемые. Ремонтируемым называется тот объект, исправность и работоспособность которого в случае возникновения отказа или повреждения подлежит восстановлению. Объект, у которого исправность и работоспособность не подлежат восстановлению называют неремонтируемым.

Ремонтопригодность – свойство объекта, заключающееся к приспособленности к предупреждению и обнаружению причин возникновения отказов (повреждений), к поддержанию и восстановлению работоспособного состояния путём проведения технического обслуживания и ремонтов.

Сохраняемость – свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и (или) транспортировки.

Живучесть энергосистемы – способность энергосистемы противостоять цепочечному развитию аварийных режимов.

Показатель надежности – количественная характеристика одного или нескольких свойств, составляющих надёжность объекта.

Нормируемый показатель надежности – показатель надежности, величина которого регламентирована нормативно-технической документацией.

Энергетическая система представляет собой большую сложную систему кибернетического типа. Она состоит из множества элементов, каждый из которых, в свою очередь, также является сложной системой (электростанции, линии электропередач и т.д.). В этих условиях возникновение отказов большого числа элементов или существенное отклонение параметров режима (частота, уровень напряжения и т.д.) могут привести не к полному прекращению электроснабжения потребителей, а к ухудшению его качества, выраженному в пониженных запасах статистической и динамической устойчивости, несоответствие показателей качества электроэнергии (ПКЭ) нормативным значениям, повышению вероятности отключения части нагрузки при действии противоаварийной автоматики и т.д. Поэтому традиционные понятия, определяющие характеристики надежности в других отраслях производства, для описания поведения энергосистем необходимо использовать с осторожностью.

Учитывая вышесказанное согласно надежность работы энергосистемы – это способность энергосистемы обеспечивать бесперебойность энергоснабжения потребителей и поддержание в допускаемых пределах показателей качества электрической энергии и тепла.

Надежность электроснабжения потребителя – это способность (свойство) электроэнергетической системы, в составе которой работает система электроснабжения потребителя, обеспечивать без ограничений поставку заявленной потребителем в соответствии с договором электрической энергии (мощности) при выполнении им всех договорных обязательств (в том числе и по оплате электроэнергии), а также при соблюдении уполномоченными субъектами электроэнергетики качественных и количественных показателей надежности функционирования электроэнергетической системы и показателей качества электрической энергии.

Надежность динамическая – свойство объекта энергетики сохранять заданные режимы функционирования при внезапных возмущениях.

3. Необходимые сведения из теории случайных событий. Теорема сложения вероятностей. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса. Понятия математического ожидания, дисперсии, среднего квадратического отклонения.

Для количественной оценки различных показателей надежности используют понятия случайного события, случайной величины и случайного процесса.

Под событием понимается всякий факт, который в результате опыта может произойти или не произойти. Например: отказ воздушной линии (ВЛ) при грозе; совпадение пиков сварочной нагрузки; отказ выключателя при отключении короткого замыкания; восстановление какого-либо элемента электрической сети за определенный промежуток времени; отказ действия релейной защиты (РЗ) при перегрузке и т.д. Такие события обладают какой-то степенью возможности: одни – большей, другие – меньшей. Чтобы качественно сравнивать между собой события по степени их возможности, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие (его вероятность).

При одновременном изучении двух или нескольких событий различают события совместные и несовместные.

События называются несовместными, если никакие два из них не могут появиться вместе, и, наоборот, события называются совместными, если они могут произойти одновременно. Пример совместного события – одновременный отказ двух и более элементов в один и тот же момент времени в относительно простой последовательной схеме. Если вероятность одного события не изменяется от того, произошло или не произошло другое событие, то такие события называются независимыми, и наоборот. Несколько событий образуют полную группу событий, если в результате опыта обязательно должно произойти хотя бы одно из них.

На основании введенных понятий формулируются следующие основные теоремы теории вероятностей, которые применяются при решении задач надежности электроснабжения.

Теорема сложения вероятностей. Суммой n событий называется сложное событие, заключающееся в появлении хотя бы одного из n. Вероятность суммы n несовместных, событий равна сумме вероятностей этих событий:

, где .

Следствие 1. Если появление хотя бы одного из n несовместных событий является достоверным событием A_n, то события A_i составляют полную группу несовместных событий, для которых выполняется соотношение

Следствие 2. Сумма вероятностей противоположных событий равна единице: ,.

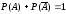Если события А и В совместны (рис. 1.1), вероятность суммы этих событий выражается формулой .

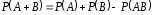Рис.1.1. Иллюстрация совместности двух событий диаграммой Венна

Вероятность суммы любого числа событий выражается

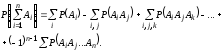
Теорема умножения вероятностей. Произведением n событий называется сложное событие, заключающееся в совместном проявлении всех n событий. Вероятность произведения независимых событий

, где .

Вероятность события , вычисленная при условии, что произошло событиеназывается условной вероятностью событияи обозначается. Для зависимых событийи

В общем виде

Формула полной вероятности. Пусть требуется определить вероятность некоторого события А, которое может произойти с одним из событий , образующих полную группу несовместных событий. Эти события будем называть гипотезами. В этом случае.

Теорема гипотез (формула Байеса). Следствием теоремы умножения вероятностей и формулы полной вероятности является теорема гипотез, или формула Байеса. Пусть имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственноПроизведён опыт, в результате которого наблюдалось событиеА. Требуется определить вероятности событий после опыта. На основании теоремы умножения и формулы полной вероятности имеем

Основные числовые характеристики случайных величин – математическое ожидание (среднее значение), дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициент вариации.

Если задан ряд распределений вероятностей для значенийслучайной величиныX, то математическое ожидание определяется по формуле

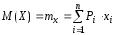
Показателями, характеризующими степень рассеяния случайной величины около своего математического ожидания, являются дисперсия и среднее квадратическое отклонение:

, ,

4. Классификация отказов ЭЭС. «Кривая жизни» электроэнергетической системы.

Противоположный безотказности термин отказ – событие, заключающееся в том, что объект перешел границу допустимой области значений его параметров из работоспособного состояния в неработоспособное и неспособен выполнять заданные функции независимо от причины этого перехода. При этом отказы классифицируются на:

полные, при которых функционирование объекта невозможно;

частичные, когда за допустимые пределы выходит один или нескольких параметров и, в зависимости от изменения его соответствующей функции возможно частичное функционирование объекта;

катастрофические, отказы, при которых происходит – внезапный полный отказ (пробой изоляции, короткое замыкание и т.д.);

внезапные, когда происходит резкое, скачкообразное изменение одного или нескольких параметров, определяющих функционирование объекта в нормальных условиях;

случайные – отказы, возникающие в фазе нормальной эксплуатации объекта в результате взаимодействия большого числа независящих друг от друга факторов;

постепенные, характеризующиеся постепенным изменением одного или нескольких заданных параметров;

параметрические, когда определяющий параметр (температура, ток срабатывания реле, сопротивление) непрерывно изменяясь во времени, достигает предельных значений, после чего система перестает выполнять заданные функции;

деградационные – постепенные частичные отказы, обусловленные естественными процессами старения, коррозии и усталости при соблюдении всех установленных правил и норм проектирования, изготовления и эксплуатации;

связанные со старением – отказы в конце периода эксплуатации в результате усталости, износа, старения материала;

независимые, то есть не обусловленные отказами других элементов (отказ подшипника при повышенном искрении коллектора машины постоянного тока);

зависимые, обусловленные отказом других элементов (отказ обмотки при разрегулировании токового реле);

каскадные, последовательные отказы двух и более элементов, при которых отказ последующего элемента является следствием предыдущего;

сбои – самоустраняющиеся отказы, приводящие к кратковременному нарушению работоспособности;

перемежающиеся – многократно возникающие, сбои одного того же характера;

приработочные, обусловленные недостаточным качеством изделия, проявляющиеся в начальной фазе его эксплуатации;

конструкционные, возникающие в результате нарушения установленных правил или норм конструирования объекта;

производственные, возникающие в результате нарушения процесса изготовления или ремонта объекта;

эксплуатационные, возникающие в результате нарушения установленных правил или условий эксплуатации объекта;

явные – отказы, которые обнаруживается сразу после их появления, без применений измерительных приборов;

неявные (скрытые) – отказы, которые не имеют внешних признаков проявления и могут быть обнаружены только с помощью измерительных приборов или средствами технической диагностики;

систематические – в результате известной взаимосвязи влияющих факторов к определённому моменту времени;

рыночные, возникающие в результате срыва плановых или договорных обязательств субъектов электроэнергетического рынка.

В качестве примера на рис. 1.2. показаны типичные случаи параметрических и катастрофических отказов. Характеристика изменения определяющего параметра П1 соответствует простейшему параметрическому отказу, а П2 – катастрофическому отказу. Характеристика П3, также соответствующая параметрическому отказу, типична для случаев, когда определяющий параметр имеет заметную периодическую составляющую, возникающую, например, из-за периодического изменения температуры, нагрузки. В этом случае после возникшего отказа возможен возврат характеристики в допустимые границы, а затем он вновь может возникнуть (перемежающийся отказ). Характеристика изменения параметра П4 кроме участков, соответствующих его плавному изменению, содержит скачок. Здесь имеет место комбинация параметрического и катастрофического отказов. Характер отказа зависит здесь от того, какое именно изменение (плавное или скачкообразное) привело к выходу параметра за допустимые границы.

Рис 1.7. Кривая жизни изделия

5. Случайные величины и законы их распределения. Экспоненциальный закон, закон Вейбулла-Гнеденко. Закон Эрланга и гамма-распределение. Закон Гаусса (нормальное распределение, усеченное нормальное распределение). Логонормальное распределение и законы распределения дискретных величин (биномиальное распределение, распределение Пуассона).

Случайной называется величина, которая в результате испытаний может принять то или иное значение, причем заранее неизвестно, какое именно.

Случайные величины могут быть дискретными и непрерывными. Непрерывными случайными величинами являются: время безотказной работы элементов, устройств, агрегатов, систем; время вынужденного простоя оборудования из-за отказов; уровень того или иного технического параметра и т.д. Дискретными случайными величинами являются: число неисправных элементов, устройств, агрегатов из общего числа находящихся в эксплуатации; число дефектных изделий в какой-либо партии продукции; количество повреждений элементов какого-либо оборудования в единицу времени и т.д.

Из-за невозможности указать, какое конкретное значение примет случайная величина в данном эксперименте, для ее характеристики применяются вероятности того, что она будет равна заданному значению или окажется в указанных пределах возможного значения. При этом используются понятия числовых характеристик распределений случайных величин.

Основные числовые характеристики случайных величин – математическое ожидание (среднее значение), дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициент вариации.

Если задан ряд распределений вероятностей для значенийслучайной величиныX, то математическое ожидание определяется по формуле

Показателями, характеризующими степень рассеяния случайной величины около своего математического ожидания, являются дисперсия и среднее квадратическое отклонение:

, ,

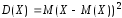Для более полного описания случайных величин вводятся понятия функции распределения F(x) и плотности распределения f(x). Функция распределения определяет для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х:

Плотность распределения непрерывной случайной величины – первая производная от функции распределения:

,

Тогда математическое ожидание и дисперсия непрерывной случайной величины определятся как

, ,.

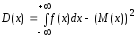Экспоненциальное распределение

- характеризуется тем, что наработка последовательной системы, состоящей из независимых элементов с экспоненциально распределенными наработками и параметрами , также имеет экспоненциальное распределение с параметром. Этому закону подчиняются отказы некоторых узлов электрических машин малой мощности (например, коллекторный узел), а также отказы некоторых типов машин малой мощности. Этот закон широко используется для описания надежности пускорегулирующей аппаратуры, элементов радиоэлектроники (диоды, конденсаторы).

Средняя наработка и дисперсия наработки такой системы равны

;

.

Поскольку интенсивность отказов такой системы постоянна, то считается, что экспоненциальное распределение описывает и "стареющие" и "молодеющие" системы. Очевидно, что описание поведения реальных систем и их элементов на основе экспоненциального распределения наработки является хотя идеализированным, но удобным с точки зрения упрощения расчетов показателей надежности на нормальном этапе эксплуатации.

Экспоненциальное распределение является частным случаем некоторых двухпараметрических распределений, к которым относятся распределения Вейбулла-Гнеденко и Эрланга.

Распределение Вейбулла-Гнеденко

также как и экспоненциальное распределение обладает свойством сохранения формы распределения наработки для последовательных систем, если параметры формы распределения элементов системы одинаковы. Графики функций для различных значений показателей формы распределения приведены на рисунке 1. Широко используется при оценке надежности механических, электромеханических узлов и элементов радиоэлектронной аппаратуры. В электрических машинах этим законом описывается надежность подшипниковых узлов, а также распределение пробивного напряжения в обмотках асинхронных двигателей.

Распределение Вейбулла двухпараметрическое, включающее параметр, определяющий масштаб, и – параметр асимметрии. Характеристики закона видоизменяются в зависимости от параметра . При  = 1 распределение Вейбулла становится экспоненциальным (=const), при >1. интенсивность отказов растет, при <1 интенсивность отказов падает по закону, близкому к гиперболическому.

Вероятность безотказной работы параллельной системы, состоящей из элементов, модели поведения которых основаны на использовании распределения Вейбулла-Гнеденко, равна

Тогда формула для определения средней наработки параллельной системы имеет вид

,

где – параметр масштаба распределения наработки параллельной системы.

При интенсивность отказов элементов систем с течением времени возрастает, а приуменьшается, что позволяет использовать данную модель для описания поведения систем на этапах приработки и старения.

P(t) t	F(t) t
f(t) t	(t) t

- Модели безотказности Вейбулла-Гнеденко при ч: 1-=0,5; 2-=1,0; 3 -=2,0; 4 -=3,0

Распределение Эрланга

является распределением суммы независимых экспоненциально распределенных с параметром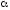случайных величин. Оно может быть также использовано для описания изменения работоспособности элемента системы, не имеющего резерва. Модель, построенная на этом распределении является более адекватной для описания поведения системы, чем экспоненциальная модель и охватывает два этапа эксплуатации, например, этапы приработки и нормальной эксплуатации. Средняя наработка до отказа рассчитывается по формуле

,

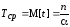дисперсия и среднее квадратическое отклонение наработки до отказа равны:

;.

Такая модель соответствует ситуации, при которой в случае отказа основного элемента системы происходит его мгновенная замена резервным элементом, не работающим до момента отказа основного.

Графики функций работоспособности и производные от нее модели поведения элементов систем на основе распределения Эрланга показаны на рисунке 2. Случайная наработка будет практически нормально распределенной при в соответствии с центральной предельной теоремой теории вероятностей.

t	t
t	t

- Модели безотказности на основе распределения Эрланга при 1/час: 1-n =1; 2-n=2; 3 -n=4; 4 -n=6

Усеченное нормальное распределение (закон Гаусса)

является двухпараметрическим распределением, у которого параметр может интерпретировать масштаб распределения, а параметр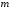– форму распределения.

Для аналитического описания используется специальная функция, так называемый интеграл вероятностей – интеграл Лапласа.

,

вычисление которого производится только численными методами.

Из вида графиков функции работоспособности и производных от нее моделей поведения элементов систем на основе усеченного нормального распределения (см. .) следует, что распределение позволяет описать поведение систем, у которых отказы наиболее вероятны как в начале, так и в некоторый заданный период эксплуатации.

t	t
t	t

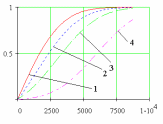
Модели безотказности на основе усеченного (слева) нормального распределения при : 1-=0; 2 -=1500; 3 -=3000; 4 -=6000

Модель безотказности, построенная на его основе, имеет возрастающую функцию интенсивности отказов, которая линейна при . Прихарактеристики усеченного нормального распределения стремятся к характеристикам нормального распределения. Практически модель безотказности на основе усеченного нормального распределения применяют, если, а иначе используют более простое в описании нормальное (неусеченное) распределение, которое дает достаточную точность при вычислении показателей безотказности.

Средняя наработка на отказ для систем их элементов, поведение которых подчиняется усеченному нормальному распределению, рассчитывается по формуле

,

дисперсия и среднее квадратическое отклонение наработки до отказа равны

;

.

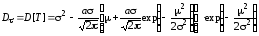Очевидно, что при параметр с пренебрежимо малой погрешностью можно принять равным единице -, а выражение. Тогда средняя наработка равна, а дисперсия наработки -.

Нормальный закон (закон Гаусса) широко используется при оценке надежности изделий, на надежность которых воздействует ряд случайных факторов, каждый из которых незначительно влияет на результирующий эффект (нет доминирующих факторов). В электрических машинах обычно нормальному закону подчиняются отказы коллекторного узла, контактных колец, а так­же щеток (иногда подшипники и изоляция):

где 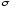– среднеквадратическое отклонение;m_х – математическое ожидание.

Нормальный закон — двухпараметрический с параметрами иm_х

Для расчета вероятности события в заданном интервале t₁, t₂ пользуются формулой

Здесь Ф(х) —интеграл вероятности (интеграл Лапласа) вида

Если используется центрированная и нормированная функция Лапласа с заменой переменных z = (t -m_x)/, то расчет вероятности безотказной работы во времени проводится по формуле

(@)

Пример: Имеется батарея аккумуляторов. Время безотказной работы бата­реи подчиняется закону Гаусса с параметрами m_x=30 ч и =4 ч. Какова вероятность безотказной работы в течение 35 ч и как обеспечить вероятность безотказной работыPс=0,35?

Решение: Воспользуемся формулой (@) и таблицей центрированной и нормированной функции (см. табл. П.VI.2 Кузнецов, Котеленец. Испытания и надежность ЭМС):

Для обеспечения более высокой надежности предусматривается резервиро­вание. При этом структурная схема надежности представляет собой параллельное соединение элементов. Определим число батарей М, необходимых для обеспечения заданной надежности:

Гамма-распределениеявляется также основой для построения моделей безотказности. Для его аналитического описания используется гамма-функция, имеющая вид

,

график которой показан на рисунке 7.



- График гамма-функции

Если верхний предел интегрирования сделать переменным , то функциональная зависимость примет вид

и будет функцией трех аргументов: параметра , которому придается физический смысл времени наработки; параметра, который определяет масштаб распределения; параметра, определяющего форму распределения.

Поскольку , то чтобы использовать гамма-функцию в качестве модели безотказности элементов системы, ее нормируют. Отношение функций и является функцией распределения, характеризующей гамма-распределенную случайную величину.

Графики функции работоспособности и производных от нее моделей поведения элементов систем на основе гамма-распределения () наглядно отражают существенные свойства данной модели поведения элементов и систем. Функция интенсивности отказов является возрастающей при и убывающей при. Призначение интенсивности отказов вначале равно нулю, а затем асимптотически приближается к некоторому постоянному значению, определяемому параметром масштаба распределения, т.е.. Привначале интенсивность отказов высокая, так как, но с течением времени становится также практически постоянной.

t	t
t	t

- Модели безотказности на основе гамма-распределения при 1/час : 1-=0.5; 2 -=1.0; 3 -=1.5; 4 -=2.0

Одним из важнейших свойств распределения является то, что если 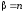, где- произвольное целое положительное число, то гамма-распределение представляет собой распределение Эрланга. Следовательно, гамма-распределение следует использовать для описания поведения элементов систем в том случае, если с помощью распределения Эрланга не удается добиться адекватного описания поведения элемента или системы.

Средняя наработка и дисперсия наработки до отказа рассчитываются по формулам:

; .

Логарифмически нормальное (логнормальное) распределениедля построения моделей безотказности используется сравнительно редко. Это можно объяснить, анализируя модели безотказности элементов систем ().

Логарифмически-нормальное распределение используется при описании надежности металлоконструкций, отказов электромашинных усилителей, некоторых типов электромашинных преобразователей и т, д. Вероятность безотказной работы

где — математическое ожидание натурального логарифма случайной величиныt, обозначающей наработку на отказ.

Расчет P(t) осуществляется с помощью специальных таблиц .

t	t
t	t

Модели безотказности на основе логарифмически нормального распределения при : 1-m= 8.883; 2 -m = 9.771; 3 -m= 10.285; 4 -m = 10.857

Интенсивность логарифмически нормально распределенных отказов системы является немонотонной функцией. В соответствии с критерием монотонности средней интенсивности отказовна этапе приработки система, отвечающая модели безотказности на основе логнормального распределения, "стареет", а на остальных этапах "молодеет" ().

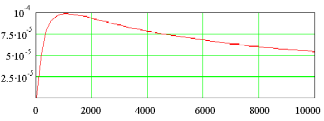t

- Изменение во времени средней интенсивности отказов системы, описанной моделью на основе логнормального распределения

Средняя наработка на отказ для систем их элементов, случайные моменты отказов которых подчиняются логнормальному распределению, рассчитывается по формуле

,

а дисперсия наработки до отказа равна

.

Несмотря на то, что распределение является двухпараметрическим, параметры формы и масштабане имеют достаточно просто интерпретируемой функциональной связи с показателями безотказности.

Биномиальное распределение Если производится серия N независимых опытов, причём вероятность появления изучаемого события в каждом опыте постоянна и равна р, а вероятность его непоявления равна , то вероятностьпоявления данного события точноi раз равна

где

Распределение Пуассона. Этот закон позволяет определить вероятность 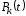наступления ровноk событий за промежуток времени t:

, ,,

где – параметр закона распределения – математическое ожидание числа событий за времяt; – интенсивность случайного события.

Закон распределения Пуассона может быть получен из биномиального распределения при достаточно больших N и малых р тогда

.

Распределение . Оно играет большую роль при решении задач, связанных с оценкой параметров надежности, определяемых при испытаниях или эксплуатации оборудования.

Рассмотрим k независимых случайных величин каждая из которых распределена по нормальному закону с параметрами, , т.е.

Сумма квадратов этих величин обозначается

,

Параметр k называется числом степеней свободы.

Плотность распределения имеет вид

, .

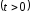6. Количественная оценка показателей надежности. Понятия вероятности безотказной работы, вероятности отказа, частоты отказов, наработки до отказа, наработки на отказ, ресурса, гамма-процентного ресурса, гамма-процентного срока сохраняемости, интенсивности отказов, коэффициенты готовности и вынужденных простоев и т.д. Виды простоев ЭЭС.

Показатели надежности характеризуют такие важнейшие свойства систем, как безотказность, живучесть, отказоустойчивость, ремонтопригодность, сохраняемость, долговечность и являются количественной оценкой их технического состояния и среды, в которой они функционируют и эксплуатируются. Оценка показателей надежности сложных технических систем на различных этапах жизненного цикла используется для выбора структуры системы из множества альтернативных вариантов, назначения гарантийных сроков эксплуатации, выбора стратегии и тактики технического обслуживания, анализа последствий отказов элементов системы.

Аналитические методы оценки показателей надежности сложных технических систем управления и принятия решения базируются на положениях теории вероятности. В силу вероятностной природы отказов оценка показателей основана на использовании методов математической статистики. При этом статистический анализ проводится, как правило, в условиях априорной неопределенности относительно законов распределения случайных значений наработки системы, а также по выборкам ограниченного объема, содержащих данные о моментах отказа элементов системы при из испытаниях или в условиях эксплуатации.

Вероятность безотказной работы (ВБР)– это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени не произойдет ни одного отказа. Вероятность P(t) – функция, убывающая см. рис.1 причем,

ВБР по статистическим данным об отказах оценивается выражением

(1)

где – статистическая оценка ВБР;– число изделий в начале испытаний, при большом числе изделий статистическая оценка практически совпадает с вероятностьюP(t); –число отказавших изделий за времяt.

Рисунок 1. Кривые вероятности безотказной работы и вероятности отказов

Вероятность отказа Q(t)– это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ. Отказ и безотказная работа – события противоположенные и несовместимые

(2)

Частота отказов a(t)– есть отношение отказавших изделий в единицу времени к первоначальному числу испытываемых изделий

(3)

где –число отказавших изделий в интервале времениt.

Частота отказов или плотность вероятности отказов может быть определена как производная по времени вероятности отказов

(4)

Знак (-) характеризует скорость снижения надежности во времени.

Средняя наработка до отказа – среднее значение продолжительности работы неремонтируемого устройства до первого отказа:

(5)

где – продолжительность работы (наработка) до отказаi-гo устройства; – число наблюдаемых устройств.

Интенсивность отказов (t) – условная плотность вероятности возникновения отказа, которая определяется как отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени

, (6)

где – число устройств, отказавших в период времени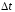;– число среднее число устройств, исправно работающих в период наблюдения;– период наблюдения.

(7)

Вероятность безотказной работы Р(t) через выразится.

Средняя наработка на отказ – среднее значение наработки ремонтируемого устройства между отказами, определяемое как среднее арифметическое:

, (9)

где 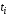– наработка до первого, второго,n-го отказа; n – число отказов от момента начала эксплуатации до окончания наблюдения. Наработка на отказ, или среднее время безотказной работы, есть математическое ожидание :

.

Параметр потока отказов – среднее количество отказов ремонтируемого устройства в единицу времени, взятое для рассматриваемого момента времени:

(11)где 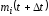– число отказовi-го устройства по состоянию на рассматриваемые моменты времени – 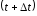иt соответственно; N – число устройств; – рассматриваемый период работы, причём.

Отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки

Среднее значение ресурса рассчитывают по данным эксплуатации или испытаний с использованием уже известного выражения для наработки:

.

Среднее время восстановления – среднее время вынужденного или регламентированного простоя, вызванного обнаружением и устранением одного отказа:

,

где – порядковый номер отказа;– среднее время обнаружения и устраненияотказа.

Коэффициент готовности – вероятность того, что оборудование будет работоспособно в произвольно выбранный момент времени в промежутках между выполнениями планового технического обслуживания. При экспоненциальном законе распределения времени безотказной работы и времени восстановлениякоэффициент готовности.

Коэффициент вынужденного простоя – это отношение времени вынужденного простоя к сумме времени исправной работы и вынужденных простоев.

Коэффициент технического использования – это отношение наработки оборудования в единицах времени за некоторый период эксплуатации к сумме этой наработки и времени всех простоев, вызванных, техническим обслуживанием и ремонтами за тот же период эксплуатации:

.

Кроме того [ГОСТ 27.002-83] определяет показатели долговечности, в терминах которых следует указывать вид действий после наступления предельного состояния объекта (например, средний ресурс до капитального ремонта; гамма-процентный ресурс до среднего ремонта и т.д.). Если предельное состояние обуславливает окончательное снятие объекта с эксплуатации, то показатели долговечности называются: полный средний ресурс (срок службы), полный гамма-процентный ресурс (срок службы), полный назначенный ресурс (срок службы).

Средний ресурс – математическое ожидание ресурса.

Гамма-процентный ресурс – наработка, в течение которой объект не достигнет предельного состояния с заданной вероятностью , выраженной в процентах.

Назначенный ресурс – суммарная наработка объекта, при достижении которой применение по назначению должно быть прекращено.

Средний срок службы – математическое ожидание срока службы.

Гамма-процентный срок службы – календарная продолжительность от начала эксплуатации объекта, в течение которой он не достигнет предельного состояния с заданной вероятностью , выраженной в процентах.

Назначенный срок службы – календарная продолжительность эксплуатации объекта, при достижении которой применение по назначению должно быть прекращено.

Показатели ремонтопригодности и сохраняемости определяются следующим образом.

Вероятность восстановления работоспособного состояния – это вероятность того, что время восстановления работоспособного состояния объекта не превысит заданного.

Среднее время восстановления работоспособного состояния – это математическое ожидание времени восстановления работоспособного состояния.

Средний срок сохраняемости – это математическое ожидание срока сохраняемости.

Гамма-процентный срок сохраняемости – это срок сохраняемости, достигаемый объектом с заданной вероятностью , выраженной в процентах.