lektsiiTAU

4. Исследование устойчивости нелинейных систем

4.1. Анализ систем методом фазовой плоскости

Для наглядного представления о сложных нелинейных процессах управления часто прибегают к понятию фазового пространства, которое было дано в пп.1.1.

Дифференциальное уравнение замкнутой системы n-го порядка можно преобразовать к системе n дифференциальных уравнений первого порядка в виде

(4.1)

с начальными условиями

при t=0,

где переменные, являющиеся искомыми функциями времени, причем может обозначать управляемую величину, а вспомогательные переменные; f и g – возмущающее и задающее воздействия.

А.М.Ляпуновым было доказано, что поведение нелинейной системы в малой окрестности положения равновесия (особой точки), т.е. «в малом», с достаточной точностью характеризуется линеаризованным дифференциальным уравнением. Этот результат обосновывает практическое применение теории линейных систем для оценки поведения нелинейной системы «в малом».

4.1.1. Фазовые траектории линейных систем

Пусть линейная система 2-го порядка описывается следующим дифференциальным уравнением:

. (4.2)

Представим уравнение (4.1) в нормальной форме Коши

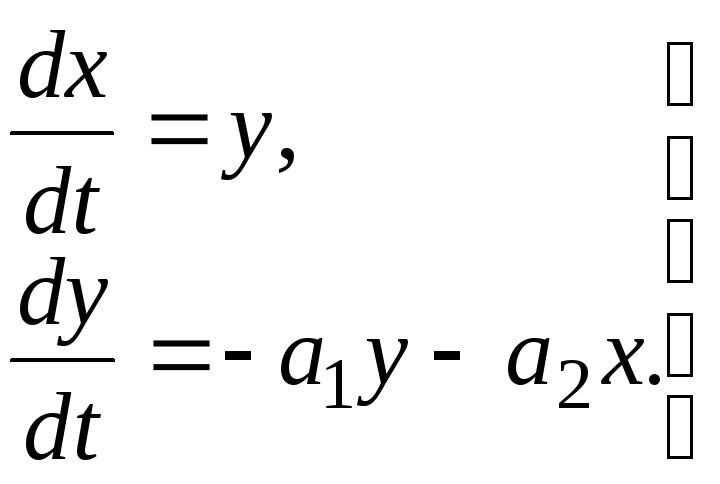(4.3)

Исключив из уравнения (4.3) время t, разделив второе уравнение на первое, получим дифференциальное уравнение фазовой траектории:

(4.4)

Решение уравнения (4.4) определяет некоторое семейство так называемых интегральных кривых на фазовой плоскости (x,y), каждая из которых соответствует одному определенному значению постоянной С.

Вся совокупность интегральных кривых представляет собой все возможные фазовые траектории, а, значит, и все возможные виды переходного процесса в данной системе при любых начальных условиях.

Вид фазовой траектории зависит от картины расположения корней характеристического уравнения. Уравнению (4.2) соответствуют корни характеристического уравнения

,

где , .

Возможны шесть случаев расположения корней:

1. корни чисто мнимые при 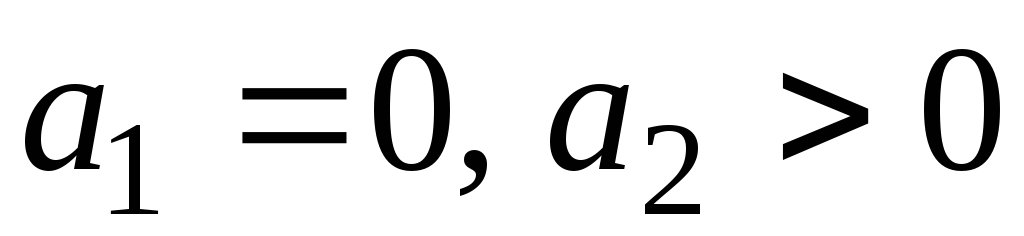(колебательная граница устойчивости);

2. корни комплексные и имеют отрицательные вещественные части при (устойчивая система);

3. корни комплексные и имеют положительные вещественные части при (неустойчивая система);

4. корни вещественные отрицательные при (устойчивая система);

5. корни вещественные положительные при (неустойчивая система);

6. корни вещественные и имеют разные знаки при (неустойчивая система); в частности, один из корней будет равен нулю при (апериодическая граница устойчивости).

Случай 1. Корни чисто мнимые:

, , .

Это консервативная система. В ней возникают незатухающие колебания (рис.4.1,а)

, (4.5)

,

с постоянной амплитудой А и начальной фазой , которые зависят от начальных условий. Для фазовой плоскости уравнения (5) представляют собой параметрические уравнения эллипса с полуосями А и ωА (рис.4.1,б).

Рис. 4.1

Уравнение эллипса

можно получить непосредственным решением дифференциального уравнения фазовых траекторий (4.4) при и , где А – постоянная интегрирования.

Каждому начальному условию () соответствует свой эллипс. Начало координат, как траектория, есть вырожденный эллипс (). Это есть особая точка, определяющая положение равновесия системы.

Особая точка в начале координат, окруженная множеством замкнутых циклов, определяемых начальными условиями, называется особой точкой типа центр. Эта особая точка устойчива по Ляпунову.

Итак, периодическим колебаниям системы (рис.4.1,а) соответствует движение изображающей точки по замкнутой кривой (рис.4.1,б).

Случай 2. Корни комплексные с отрицательными вещественными частями:

,

.

В этом случае система асимптотически устойчива, имеют место затухающие колебания (рис.4.2,а):

(4.6)

.

Параметры А и определяются из начальных условий:

при t=0.

Рис. 4.2

Значения x и y не возвращаются за период колебаний к прежним, а становятся меньше. Это дает на фазовой плоскости (x,y) кривую (рис.4.2,б), которая за один оборот не возвращается в прежнюю точку М₀, а подходит ближе к началу координат.

Особая точка (0,0), к которой сходятся все фазовые траектории при любых начальных условиях, называется устойчивым фокусом (или центром притяжения).

Но угол вхождения траектории в фокус (0,0) установить невозможно, т.к. в точке (0,0) не существует.

Итак, затухающим колебаниям системы (рис.4.2,а) отвечают фазовые траектории в виде спиралей, по которым изображающая точка приближается к началу координат (рис.4.2,б).

Случай 3. Корни комплексные с положительными вещественными частями:

,

.

В этом случае система неустойчива, в ней имеют место расходящиеся колебания (рис.4.3, а):

(4.7)

Значения x и y не возвращаются за период колебаний к прежним, а становятся больше.

Рис. 4.3

Изображающая точка движется по тем же спиралям, но только все время удаляясь от начала координат (0,0). Положение равновесия (x=0, y=0) неустойчиво. Достаточно небольшого отклонения от начала координат, чтобы началось безграничное нарастание отклонения и его скорости.

Особая точка (0,0) в этом случае называется неустойчивым фокусом (или центром отталкивания).

Случай 4. Корни вещественные отрицательные:

.

В этом случае система устойчива и имеет место апериодический процесс:

, (4.8)

где .

Возможны два варианта протекания такого процесса (кривые 1 и 2 на рис.4.4,а). Фазовая плоскость заполнена семейством интегральных кривых параболического типа. Каждая интегральная кривая состоит из трех фазовых траекторий. Одной из них является состояние равновесия (особая точка (0,0)), а двум другим, представляющим полуветви парабол за вычетом нулевой точки, соответствуют движения, неограниченно приближающиеся к состоянию равновесия.

Рис. 4.4

Все интегральные кривые за исключением прямой касаются в начале координат прямой . Прямые получаются из уравнений (4.8) при или (обращении одного из корней в нуль).

Все фазовые траектории вливаются в начало (0,0) координат фазовой плоскости. Однако, изображающая точка М не попадает в начало координат в конечное время, приближается асимптотически. Особая точка (0,0) такого типа называется устойчивым узлом.

Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.

Случай 5. Корни вещественные положительные:

.

В этом случае система неустойчива. Имеет место расходящийся апериодический процесс, определяемый уравнениями:

. (4.9)

Кривые переходного процесса и фазовые траектории изображены на рис. 4.5.

Рис. 4.5

Особая точка (0,0) данного типа называется неустойчивым узлом.

Случай 6. Корни вещественные и имеют разные знаки

.

В этом случае также имеет место расходящийся апериодический процесс (рис.4.6,а):

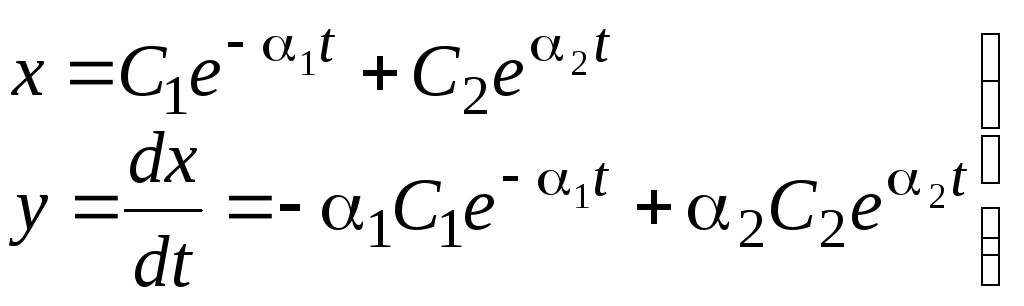, (4.10)

но картина фазовых траекторий здесь иная (рис.4.6,б).

Рис. 4.6

Так как , то введем обозначение . Для простоты построений рассмотрим случай . Согласно (4.3), получим уравнения системы

,

и, согласно (4.4), уравнение фазовых траекторий

.

Проинтегрировав последнее выражение, получим

.

Это уравнение представляет собой семейство равносторонних гипербол, изображенных на рис. 4.6,б.

Значение С определяется начальными условиями. Пусть С=0, тогда

,

т.е. . Эти прямые являются асимптотами семейства гипербол, проходящими через особую точку (0,0) и являющимися интегральными кривыми. Каждая асимптота состоит из трех фазовых траекторий (одна полупрямая, начало координат, вторая полупрямая). Все остальные интегральные кривые составляют одну фазовую траекторию.

Если начальные условия такие, что изображающая точка лежит на асимптоте, то она будет апериодически приближаться к началу координат, а по всем остальным фазовым траекториям она будет удаляться от начала координат.

Особая точка (0,0) данного типа называется седлом. Она соответствует положению неустойчивого равновесия.

Частному случаю , когда один из корней уравнения (4.2) будет равен нулю, соответствует картина фазовых траекторий, изображенная на рис.4.7. На рисунке 4.7,а представлен случай, когда один корень равен нулю, один корень левый. Уравнения фазовых траекторий запишутся в виде

,

отсюда,

.

Здесь особых точек нет, вся ось х есть множество точек равновесия (безразличия).

На рисунке 4.7,б представлен случай, когда один корень равен нулю, один корень правый.

Рис. 4.7

Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис.4.5,б или типа рис.4.6,б, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.

4.1.2. Фазовые траектории нелинейных систем

Реальные системы автоматического управления можно считать линейными лишь в предположении малости отклонений переменных от их значений в определенном установившемся состоянии.

За пределами указанной области вследствие значительного отклонения характеристик от линейных картина фазовых траекторий может сильно измениться и стать качественно иной.

Отметим два основных признака, которые отличают нелинейные системы от линейных:

1. существование в нелинейных системах предельных циклов;

2. различный характер движения в разных областях фазового пространства для одной и той же системы.

Вся фазовая плоскость нелинейной системы разбивается на области различной топологической структуры, которые разграничиваются особыми траекториями: сепаратрисами и предельными циклами. Внутри области система ведет себя качественно одинаково и с течением времени достигает одного и того же установившегося режима. Установившиеся режимы нелинейных систем не зависят от начальных условий.

Для нелинейных систем различают три типа особых траекторий:

1. особая точка или отрезок (точка равновесия);

2. предельный цикл;

3. сепаратриса («усы» седел).

Особая точка или особый отрезок.

В системах с нелинейными элементами типа «зона нечувствительности» и «сухое трение» существуют области застоя, когда установившемуся состоянию при данных внешних условиях соответствует не одна точка, а целая область возможных равновесных состояний системы. На фазовой плоскости это выражается в том, что особая точка вытягивается в особый отрезок (рис.4.8).

Примечание. У линейной системы одна особая точка, а у нелинейной системы их может быть несколько, а также отрезки и области покоя.

Рис. 4.8

Предельный цикл.

Если линейная система неустойчива, то процесс в ней расходится неограниченно. В нелинейной же системе из-за нелинейности характеристик расходящийся процесс может быть ограниченным: амплитуда расходящихся колебаний может увеличиваться только до определенного значения, а затем оставаться постоянной. В системе устанавливаются устойчивые периодические движения – автоколебания. На фазовой плоскости автоколебаниям соответствует изолированная замкнутая кривая, которая называется предельным циклом.

Картина фазовых траекторий для такой системы изображена на рис.4.9,а.

б)

Рис. 4.9

Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе (рис.4.3,б), но далее все они расходятся не до бесконечности, а приближаются асимптотически к замкнутому контуру ограниченных размеров. К нему же приближаются и все спирали, находящиеся вне контура. Это соответствует картине переходных процессов, изображенных на рис.4.9,б.

Такого вида замкнутый контур, представляющий собой наиболее важный для теории тип особых линий на фазовой плоскости, называется устойчивым предельным циклом.

Размеры предельного цикла А и В представляют амплитуды колебаний самой величины х и скорости ее изменения . Для определения периода автоколебаний необходимо решить дифференциальные уравнения.

Случаю устойчивости системы «в малом» и неустойчивости «в большом» (рис.4.10,а) соответствует картина фазовых траекторий, изображенная на рис.4.10,б.

а)

Рис. 4.10

Граница начальных условий, до которой система устойчива, имеет вид неустойчивого предельного цикла, от которого в обе стороны удаляются спиралевидные фазовые траектории. Это второй важный тип особых линий, определяющий устойчивость системы «в малом» и неустойчивость «в большом».

Заметим, что в этом случае может быть также еще более удаленный устойчивый предельный цикл (рис.4.11,а), соответствующий автоколебаниям с большой амплитудой.

Это соответствует переходным процессам, изображенным на рис.4.11,б.

а б

Рис. 4.11

Такие же принципиальные качественные изменения картины фазовых траекторий при достаточно больших отклонениях могут наблюдаться и в случаях апериодических процессов (рис.4.5,б и 4.6,б), включая превращения их в автоколебательные и наоборот. Например, картине переходных процессов, представленной на рис.4.12,б, соответствует картина фазовых траекторий на рис.4.12,а.

а б

Рис. 4.12

Примечание. В консервативной линейной системе нет предельного цикла (особых траекторий), а каждая траектория определяется начальными условиями.

Сепаратриса («усы» седел).

Для линейной системы, находящейся на границе устойчивости (при чисто мнимых корнях), картина фазовых траекторий, изображенная на рис.4.1,б, может иметь место лишь вблизи состояния установившегося режима (0,0). При больших отклонениях, если линейность характеристик звеньев системы нарушается, картина фазовых траекторий будет другой. Один из возможных вариантов изменения фазовых траекторий при больших отклонениях в этом случае показан на рис.4.13.

Рис. 4.13

Здесь, кроме особой точки (0,0) типа центра, появляются два седла С₁ и С₂, что приводит фактически к неустойчивости системы. Но может иметь место и устойчивый предельный цикл. Особые линии такого типа, как С₁А₁С₂ и С₂А₂С₁, на фазовой плоскости называются сепаратрисами (третий тип особых линий).

В окрестности особых точек С₁ и С₂ сепаратрисы являются асимптотами, поэтому их также называют «усами» седел.

Сепаратриса отделяет друг от друга области, заполненные фазовыми траекториями различных видов.

В фазовом пространстве выделяются такие области значений координат изображающей точки М, в каждой из которых с течением времени достигается лишь один из возможных установившихся режимов. Эти области называются областями притяжения этих режимов. Границы этих областей образуются неустойчивыми предельными циклами и сепаратрисами седел.

Примечание. Если характеристики нелинейного элемента представляют собой кусочно-линейную функцию, то последняя изображается в виде ломаных линий иногда с разрывами (например, релейные характеристики).

На фазовой плоскости угловым точкам и точкам разрыва этих ломаных соответствуют некоторые линии, которые называются линиями переключения. Переключение меняет дифференциальные уравнения системы, т.е. ее фазовый портрет (топологию, качественную картину движения). Поэтому справа от линии переключения фазовый портрет соответствует одному состоянию системы, а слева – другому.

Таким образом, разбивая всю фазовую плоскость на топологически однородные области, получают полную качественную картину всех возможных движений системы.

По виду фазового портрета можно сделать важные выводы о поведении системы. Если на каком-либо участке фазовая траектория линейна, то в этом диапазоне переменная изменяется экспоненциально. Если на фазовой плоскости имеется несколько устойчивых особых точек, то в системе могут существовать несколько устойчивых состояний, причем установление одного из них определяется начальными условиями. Область фазовой траектории, из которой все траектории приходят к одной устойчивой особой точке, отделяется от других сепаратрисами. Если на фазовой плоскости имеется замкнутая фазовая траектория, то в системе могут существовать стационарные устойчивые колебания.