Уравнения, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим 3 типа уравнений, допускающих понижение порядка.
-
Пусть дано уравнение y’’=f(x). Порядок можно понизить, введя новую функцию p(x), положив y’=p(x). Тогда y’’=p’(x) и получаем ДУ первого порядка: p’=f(x). Решив его, т.е. найдя функцию р=р(х), решим уравнение у’=р(х). Получим общее решение заданного уравнения y’’=f(x).
-
Пусть дано уравнение y’’=f(x;y’), не содержащее явно искомой функции у.
Обозначим
у’=р,
где р=р(х)
– новая неизвестная функция. Тогда
у’’=p’
и уравнение y’’=f(x;y’)
принимает
вид
р’=f(x;p).
Пусть
р=
-
общее решение
полученного
ДУ первого порядка. Заменяя функцию р
на у’,
получаем ДУ: y’=
.
Оно имеет вид
y’’=f(x).
Для отыскания у достаточно проинтегрировать
последнее уравнение. Общее решение
уравнения y’’=f(x;y’)
будет иметь вид
у=
.
Частным
случаем уравнения y’’=f(x;y’)
является уравнение y’’=f(y’),
не содержащее также и независимую
переменную х.
Оно интегрируется тем же способом:
y’=p(x),
y’’=p’=
.
Получаем уравнение p’=f(p)
с
разделяющимися переменными.
-
Рассмотрим уравнение y’’=f(y;y’), которое не содержит явно
независимой переменной х.
Для понижения порядка уравнения введем новую функцию р=р(у), зависящую от переменной у, полагая y’=p. Дифференцируем это равенство по х, учитывая, что р=р(у(х)):
,
т.е.
=
.
Теперь уравнение y’’=f(y;y’)
запишется
в виде
=f(y;p).
Пусть
р=
является общим решением этого ДУ первого
порядка. Заменяя функцию р(у)
на y’,
получаем y’=
- ДУ с разделяющимися переменными.
Интегрируя его, находим общий интеграл
уравнения y’’=f(y;y’):
.
Частным
случаем уравнения y’’=f(y;y’)
является ДУ y’’=f(y).
Такое уравнение решается при помощи
аналогичной подстановки: y’=p(y),
y’’=
.
Линейные дифференциальные уравнения высших порядков.
Основные понятия
Уравнения вида
,
где
-
заданные функции (от х),
называется линейным
дифференциальным уравнением n-го
порядка.
Оно
содержит искомую функцию у
и все ее производные лишь в первой
степени. Функции
называются
коэффициентами
уравнения, а функция g(x)
– его свободным
членом.
Если
свободный член g(x)=0,
то уравнение
называется линейным
однородным
уравнением, иначе – неоднородным.
Разделив
уравнение
на
и
обозначив
запишем
уравнение
в виде приведенного:
Линейные однородные дифференциальные уравнения второго порядка
Рассмотрим ЛОДУ второго порядка:
И установим некоторые свойства его решений.
Теорема:
Если
функции
и
являются частными решениями уравнения
,
то решением этого уравнения является
также функция
,
где
и
- произвольные постоянные.
Подставим
функцию
и ее производные в левую часть ЛОДУ
.
Получаем:
так
как функции
и
-
решения уравнения 
и, значит, выражения в скобках тождественно
равны 0.
Таким
образом, функция
также
является решением уравнения
.
Из
теоремы, как следствие, вытекает, что
если
и
- решения уравнения
,
То
решениями его будут также функции у=
+
и
у=с
.
Функция
содержит две произвольные постоянные
и является решением уравнения
.
А для ответа на вопрос, может ли эта функция являться общим решением, введем понятие линейной зависимости и линейной независимости функций.
Функции
и
называются
линейно
независимыми
на интервале (a;b),
если равенство
,
где
,
R,
выполняется тогда и только тогда, когда
=
=0.
Если
хотя бы одно из чисел
или
отлично от 0 и выполняется равенство
,
то функции
и
называются
линейно
зависимыми.
Средством изучения линейной зависимости системы функций является так называемый определитель Вронского или вронскиан.
Для
двух дифференцируемых функций
и
вронскиан
имеет вид
W(x)=
.
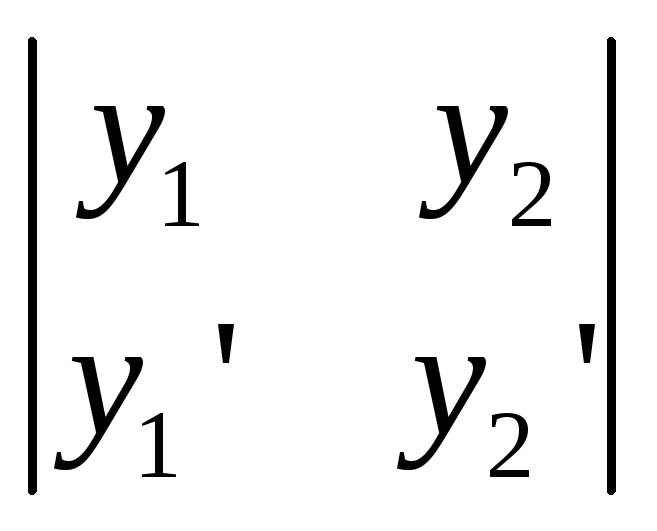Имеют место следующие теоремы.
Теорема:
Если дифференцируемые функции
(х)
и
(х)
линейно зависимы на (a;b),
то определитель Вронского на этом
интервале тождественно равен 0.
Так
как функции
и
линейно зависимы, то в равенстве
значение
или
отлично от 0. Пусть
0,
тогда
=
;
поэтому для любого х
(a;b)
W(x)=
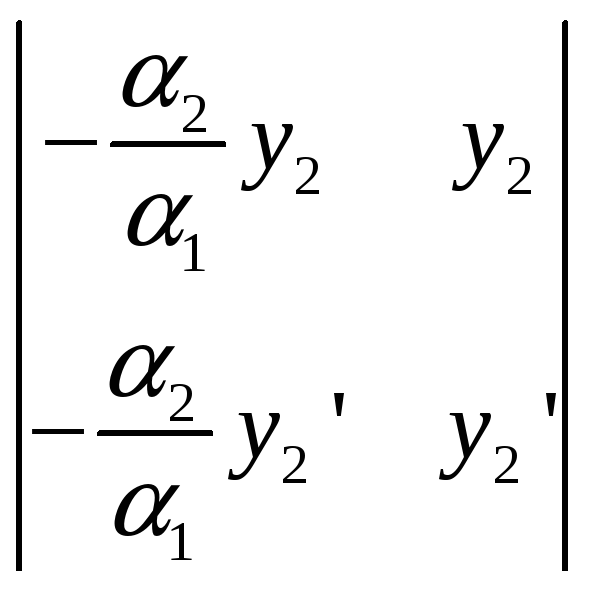=0.
Теорема:
Если функции
(х)
и
(х)
- линейно независимые решения уравнения
на (a;b),
то определитель Вронского на этом
интервале нигде не обращается в нуль.
Интегрирование ДУ второго порядка с постоянными коэффициентами
Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.
Пусть дано ЛОДУ второго порядка
,
Где p и q постоянны.
Для
нахождения общего решения уравнения
достаточно найти два его частных решений,
образующих фундаментальную систему.
Будем
искать частные решения уравнения
в
виде
,
где
k
– некоторое число. Дифференцируя эту
функцию 2 раза и подставляя выражения
для у,
у’ и
у’’
в
уравнение
,
получим:
,
т.е.
,
или
=0
(
).
Уравнение
=0
(
)
называется характеристическим уравнением
ДУ
.
При его решении возможны следующие три случая
Случай
1:
Корни уравнения
и
уравнения
=0
(
).
Действительные и различные:
(D
=
- q
> 0).
В
этом случае частными решениями уравнения
являются функции
=
и
=
.
Они образуют фундаментальную систему
решений (линейно независимы), т.к. их
вронскиан
W(x)
=
=
Следовательно,
общее решение уравнения
,
Случай
2:
Корни
и
характеристического уравнения
=0
(
),
действительные равные:
.
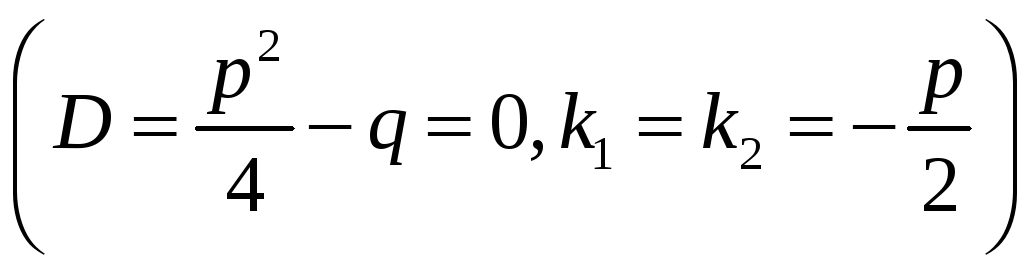В
этом случае имеем лишь одно частное
решение
.
Покажем,
что наряду с
решением уравнения
будет
и
.
Действительно,
подставим функцию
в уравнение
.
Имеем:
+
Но
,
т.к.
есть корень уравнения
=0
(
)
;
,
т.к. по условию
.
Поэтому
,
т.е. функция
является решением уравнения
.
Частные
решения
и
образуют фундаментальную систему
решений:
.
Следовательно, в этом случае общее
решение ЛОДУ
имеет вид
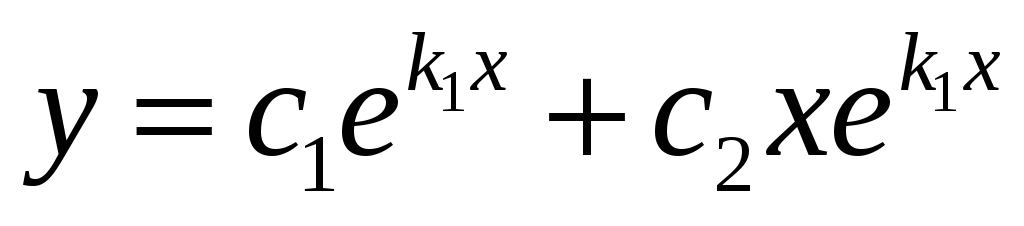
Случай
3:
Корни
и
уравнения
=0
(
)
комплексные:
,
В
этом случае частными решениями уравнения
являются функции
и
.
По формулам Эйлера:
,
Имеем
,
.
Найдем
два действительных частных решения
уравнения
.
Для этого составим две линейные комбинации
решений для
и
:
и
.
Функции
и
являются решениями уравнения
,
что следует из свойств решений ЛОДУ
второго порядка. Эти решения
и
образуют фундаментальную систему
решений, т.к.
.
Поэтому общее решение данного уравнения
запишется в виде
или
Линейные неоднородные дифференциальные уравнения (ЛНДУ)
Структура общего решения ЛНДУ второго порядка
Рассмотрим ЛНДУ второго порядка
,
где
,
,
– заданные, непрерывные на (a;b)
функции. Уравнение
,
левая
часть которого совпадает с левой частью
ЛНДУ
, называется соответствующим
ему однородным
уравнением.
Теорема (структура общего решения ЛНДУ):
Общим
решением у уравнения
является сумма его произвольного
частного решения
и общего решения
соответствующего однородного уравнения
,
т.е.
.
Убедимся,
что функция
– решение уравнения
.
Так как
есть решение уравнения
,
а
–
решение уравнения
,
то
и
.
В таком случае имеем:
Это
означает, что функция
является решением уравнения
.
Покажем теперь, что функция
является
общим решением уравнения
. Для этого надо доказать, что из решения
можно выделить единственное частное
решение, удовлетворяющее заданным
начальным условиям
,
.
Продифференцировав
функцию
и
подставив начальные условия в данную
функцию и ее производную, получим систему
уравнений:
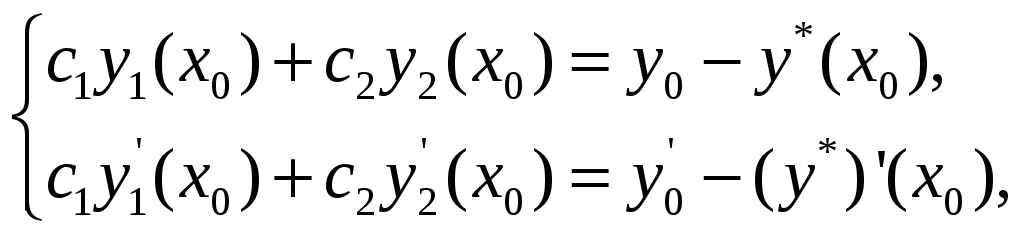
где
,
с неизвестными
и
. Определителем этой системы является
определитель Вронского
для функции
и
в точке
.
Функции
и
линейно независимы, т.е.
.
Следовательно, система имеет единственное
решение:
и
.
Решение
является частным решением уравнения
,
удовлетворяющим заданным начальным
условиям
,
.
Теорема доказана.