19. Элементарная ячейка (параллелепипед повторяемости) кристаллической структуры, ее параметры и правила выбора.

Характеристическая ячейка, наиболее полно отражающая все особенности трехмерной решетки, — это параллелепипед, построенный на трех кратчайших неколлинеарных трансляционных векторах, совпадающих с особыми направлениями максимальной симметрии т. е. с на­правлением кристаллографических координатных осей, а при отсутствии особых направлений — с узловыми рядами. Например, в триклин-ной решетке ребра характеристической ячейки рекомендуется совмещать с такими трансляционными векторами, которые обеспечат ее примитивность, а следовательно, минимальный объем. В моноклинной решетке одно ребро ячейки совмещают с единственным особым направлением ( —), а два других ребра направляют по трансляционным векторам, лежащим в плоскости, перпендикулярной этому особому направлению (т. е. в плоскости симметрии решетки, а следовательно, по векторам повышенной симметрии). Отсутствие особых направлений в плоскости косоугольной грани не накладывает ограничений на выбор ребер ячейки, поэтому узлы такой грани будут располагаться только в ее вершинах. Выбранный таким образом параллелепипед подчинен кристаллографической координатной системе, имеет минимальную площадь и называется элементарной ячейкой или ячейкой Браве. Поскольку форму ячейки Браве определяет координатный репер, семь разных по симметрии реше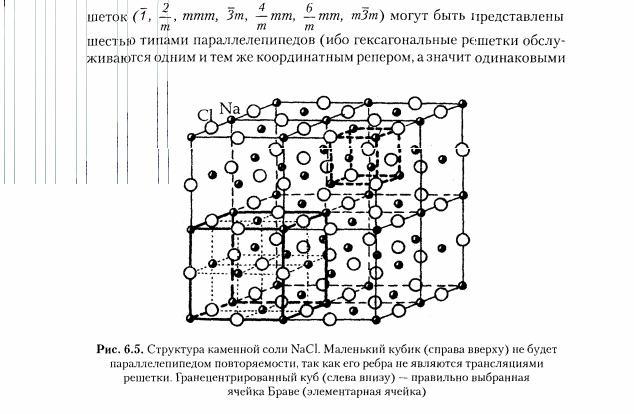

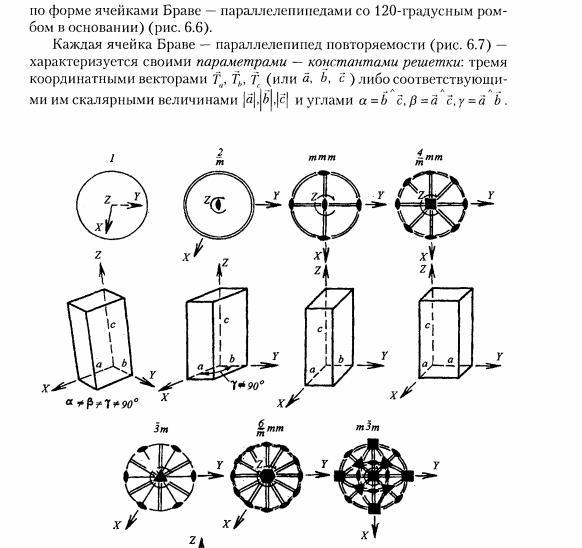
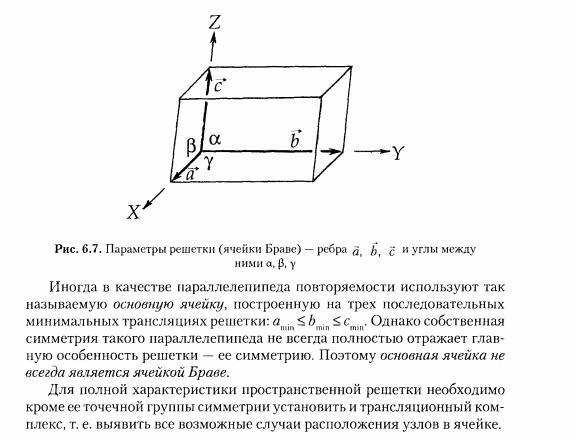
20. Решетки Бравэ, их обозначения. Элементы симметрии бесконечных фигур, их сочетания.

БРАВЕ РЕШЁТКИ - классификация решёток параллельных переносов, учитывающая как их точечную, так и параллельно-переноснуюсимметрию. Всего существует 14 типов Б. р., названных по имени О. Браве (A. Bravais), строго обосновавшего эту классификацию. Решёткой наз. совокупность точек пространства (узлов) с целочисленными координатами относительно фиксированной системы координат, построенной на трёх базисных векторах а, b, с - осн. репере решётки. Для представления решёток используют репер Браве - систему координат, построенную на векторах решётки, совпадающих с наиб. симметричными в данной голоэдрии направлениями. Выбор таких векторов может быть неоднозначным и существуют дополнит. правила: сначала выбираются векторы, совпадающие с осями симметрии, затем - самые короткие векторы, не образующие острых углов между собой. Параметры реперов Браве (длины а, 6, с, его векторов и углы между векторами b и с, а ис, а и b соответственно) в каждой из 7 сингоний (совокупностей решёток с одинаковой голоэдрией) имеют ограничения, указанные в табл., в к-рой также приведены обозначения всех Б. р., распределённые по соответств. сингониям.

	Сингония	Параметры репера Браве	Обозначения Браве решёток
			международные	физические
	Триклинная
	Моноклинная
	Ромбическая
	Ромбоэдрическая
	Тетрагональная
	Гексагональная
	Кубическая

Параллелепипед, построенный на репере Браве, наз. параллелепипедом Браве. Если узлы решётки находятся только в вершинах параллелепипеда Браве, то он и соответствующая ему решётка наз. примитивными (Р-решётки). В нек-рых решётках в параллелепипед Браве попадают дополнит. узлы. Такие параллелепипеды (и решётки) возможны 4 сортов: 1) базоцентрированные С или бокоцентрированные В (А) - дополнит. узлы в центрах граней, построенных на векторах а и b, а и с, b и с соответственно и на параллельных им гранях; 2) дважды центрированные гексагональные (ромбоэдрические) R - дополнит. узлы на главной диагонали параллелепипеда Браве в точках с координатами ²/₃, ¹/₃, ¹/₃ и ¹/₃, ²/₃, ²/₃ ; 3) гранецентрированные F - дополнит. узлы в центрах всех граней параллелепипеда Браве; 4) объёмноцентрированные I - дополнит. узел в центре параллелепипеда Браве.

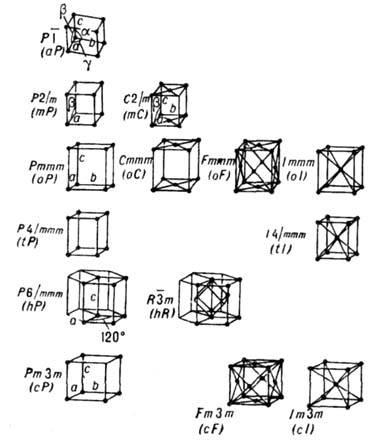
Две решётки относятся к одному и тому же типу Браве, если их параллелепипеды Браве одинаковы и имеют одинаковую центрировку. На рис. представлены все типы Б. р., причём в одной строке расположены решётки с одинаковыми параллелепипедами Браве, а в одном столбце - решётки с одинаковым типом центри-ровок. Около каждого параллелепипеда Браве указан символ соответствующей группы Браве - полной совокупности преобразований симметрии соответствующей решётки. Имеется 14 абстрактно-неизоморфных таких групп (14 из 73 симморфных фёдоровских групп). Группы Браве - основа теоретико-группового определения типов Б. р.: две решётки относятся к одному и тому же типу Браве, если их полные группы преобразований симметрии изоморфны. В скобках на рис. приведены стандартные символы соответствующих типов Б. р. В двумерном случае (в случае плоскости) имеется 5 типов Б. р.: р2, р2тт, с2тт, p4mm, р6тm.

Элементы симметрии бесконечных фигур, их сочетания.

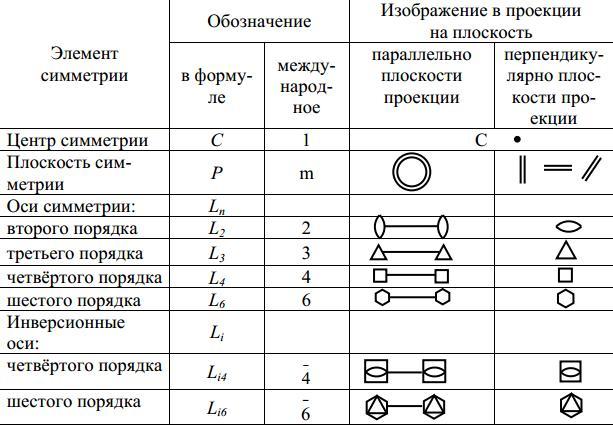
Одним из свойств, присущих кристаллам, является симметрия. Симметрия - (от греческого «соразмерность») - закономерная повторяемость равных фигур или равных частей одной и той же фигуры в пространстве. Две фигуры называются равными, если расстояние между двумя любыми точками одной фигуры равно расстоянию между двумя соответственными точками другой. К элементам симметрии относятся центр симметрии, оси и плоскости симметрии. Центр симметрии – воображаемая точка внутри фигуры, в которой пересекаются и делятся пополам все прямые, соединяющие соответствен-ные точки на поверхности фигуры (рис. 1). В формуле симметрии обозначается символом С (табл. 1). В многограннике, обладающем центром симметрии, каждой грани отвечает другая грань, равная и параллельная первой. Плоскость симметрии – воображаемая плоскость, разделяющая фигуру на две зеркально-равные части (рис. 2). В формуле симметрии обозначается символом P (табл. 1). Плоскости симметрии проходят перпендикулярно граням и рёбрам через их середины или же идут вдоль рёбер, образуя равные углы с одинаковыми гранями и рёбрами. При подсчёте количества плоскостей симметрии в исследуемой фигуре нужно держать её в одном положении, для того чтобы одну и ту же плос-кость не сосчитать несколько раз.Ось симметрии – воображаемая прямая линия (ось), при вращении вокруг которой на 360 фигура совпадает сама с собой n раз. Количество совпадений n – отвечает порядку оси симметрии. Например, если при вращении на 360 вокруг оси фигура совпадает сама с собой через каждые 180, то есть дважды, то порядок оси симметрии – второй; если – через 120, то есть трижды, – третий и т.п. В формуле симметрии ось обозначается символом Ln (табл. 1). В кристаллических многогранниках и их структурах возможны оси симметрии второго, третьего, четвёртого и шестого порядка. Ось симметрии инверсионная – прямая линия (ось), при повороте вокруг которой на определённый угол и последующем её отражении в цен-тральной точке, фигура совпадает сама с собой. В формуле симметрии обозначается символом Lin. Существуют инверсионные оси симметрии четвёртого и шестого порядка.

Существует ряд теорем, позволяющих строго математически вывести все возможные совокупности элементов симметрии.

Теорема 1. Линия пересечения двух плоскостей симметрии есть ось симметрии, причём угол поворота вокруг этой оси в два раза больше угла между плоскостями.

Теорема 2. Точка пересечения чётной оси симметрии L2n с перпендикулярной ей плоскостью симметрии есть центр симметрии С.

Теорема 3. Если есть ось симметрии n-го порядка и перпендикулярная ей ось второго порядка, то всего таких осей должно быть n.

Теорема 4. Если есть ось симметрии n-го порядка и вдоль нее проходит плоскость симметрии, то таких плоскостей имеется n.

Теорема 5. Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

Теорема 6. Плоскость, проходящая вдоль четной инверсионной оси симметрии, приводит к появлению оси второго порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.