14

Типовой расчет

Для экономических специальностей по теме:

Элементы математической статистики

Вариант № a

Задание 1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.

1	2	3	4	5	6	7	8	9	10
3,37	3,45	3,86	3,63	3,63	3,75	3,67	3,99	4,11	3,77
11	12	13	14	15	16	17	18	19	20
3,98	4,18	4,45	4,11	4,34	4,04	3,79	3,88	4,27	4,15
21	22	23	24	25	26	27	28	29	30
4,06	4,35	4,38	4,59	4,26	3,89	3,55	3,79	4,21	4,09
31	32	33	34	35	36	37	38	39	40
3,84	3,94	3,81	3,90	3,67	3,92	3,36	3,79	3,64	3,75
41	42	43	44	45	46	47	48	49	50
3,97	4,15	4,51	4,55	4,36	4,06	3,78	3,87	3,55	3,67

Решение. Первичная обработка обычно начинается с отыскания минимального x_min и максимального x_max значений исходных статистических данных, а также вычисления размаха варьирования R=x_max–x_min. Для исходных данных находим:

xmin=3,36

xmax=4,59

R=1,23

Следующий этап первичной обработки статистических данных – группировка. Для этого промежуток [x_min, x_max] разбивают на m интервалов (чаще всего одинаковой длины) и подсчитывают число n_j значений, которые попали в j-й интервал. Обычно выбирают m=720 интервалов. На практике для определения длины интервала часто используют эмпирическую формулу Стэрджеса:

,

где n – объем исходного статистического ряда.

За начало первого интервала рекомендуется принимать величину, равную (x_min–h/2). Тогда, если x₁ – начало первого интервала, то x₂=x₁+h – начало второго и т.д. Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или большим x_max. После установления шкалы интервалов приступают к группировке исходных статистических данных.

В соответствии с полученными выше результатами, определяем оптимальную длину интервала:

.

После этого строим систему интервалов и создаем интервальный вариационный ряд:

№	x-h/2	x+h/2	xi	ni	wi	ni/h
1	3,27	3,45	3,36	3	0,06	17
2	3,45	3,63	3,54	3	0,06	17
3	3,63	3,81	3,72	13	0,26	72
4	3,81	3,99	3,9	11	0,22	61
5	3,99	4,17	4,08	8	0,16	44
6	4,17	4,35	4,26	6	0,12	33
7	4,35	4,53	4,44	4	0,08	22
8	4,53	4,71	4,62	2	0,04	11

В данной таблице w_i = n_i/n – относительные частоты, n_i/h – плотность частот.

С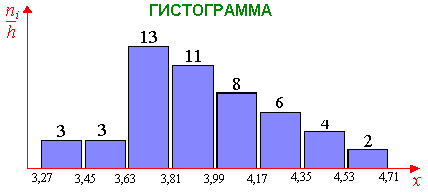троим гистограмму частот построенного вариационного ряда. Для этого вдоль оси абсцисс отложим отрезки, изображающие интервалы вариационного ряда, и на этих отрезках построим прямоугольники с высотами, равным частотам соответствующего интервала.

С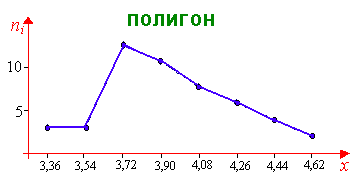троим полигон относительных частот построенного вариационного ряда. Для этого в прямоугольной системе координат нанесем точки (x_i,w_i) (эти точки являются серединами соответствующих интервалов). Затем эти точки соединим отрезками.

Вычисление среднего арифметического, дисперсии и, особенно, моментов высших порядков непосредственно по их формулам приводит к громоздким вычислениям, если числовые значения достаточно велики. Поэтому воспользуемся упрощенным методом расчета моментов. Для этого все значения дискретного вариационного ряда преобразуем по формуле

.

Постоянные h и C выбираются произвольно. Обычно в качестве C выбирают значение, которое имеет наибольшую частоту или занимает среднее положение в ряду. В качестве h можно взять длину интервала. Для полученного дискретного вариационного ряда новые переменные получим следующим образом

.

Среднее арифметическое вычисляется по формуле

.

По упрощенному методу с начала вычисляется среднее значение для новой переменной u, а затем находится искомое значение по формуле

.

Дисперсия вычисляется по формуле

.

По упрощенному методу с начала вычисляется дисперсия для новой переменной D(u), а затем находится искомое значение D(x) по формуле

.

Составим таблицу

xi	ni	ui	ni ui	ni ui2
3,36	3	–3	–9	27
3,54	3	–2	–6	12
3,72	13	–1	–13	13
3,9	11	0	0	0
4,08	8	1	8	8
4,26	6	2	12	24
4,44	4	3	12	36
4,62	2	4	8	32
Сумма	50	–	12	152

В соответствие с данными таблицы среднее значение

,

а также дисперсию

.

Задание 2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда:

x	582-589	589-596	596-603	603-610	610-617	617-624	624-631	631-638	638-645	645-652
n	4	5	6	12	21	17	9	7	5	4

а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания и дисперсии с доверительной вероятностью =0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости =0,05.

Решение. а) Вычислим основные числовые характеристики данного вариационного ряда, используя упрощенный метод расчета моментов. Для этого вместо интервального ряда введем дискретный, записав вместо интервалов только середины интервалов, а результаты занесем в таблицу. По упрощенному методу вводим новую переменную

.

Далее, в соответствии с данными таблицы получаем

,

.

Однако выборочная дисперсия является смещенной оценкой, т.е. она дает заниженное значение дисперсии генеральной совокупности. Поэтому вместо выборочной дисперсии используют исправленную выборочную дисперсию

.

В данном случае

.

Тогда среднеквадратичное отклонение равно .

xi	ni	ui	niui
585,5	4	–4	–16	64	–256	1024
592,5	5	–3	–15	45	–135	405
599,5	6	–2	–12	24	–48	96
606,5	12	–1	–12	12	–12	12
613,5	21	0	0	0	0	0
620,5	17	1	17	17	17	17
627,5	9	2	18	36	72	144
634,5	7	3	21	63	189	567
641,5	5	4	20	80	320	1280
648,5	4	5	20	100	500	2500
			41	441	647	6045

Доверительным интервалом (,) для статистического параметра  называется интервал, который с заданной вероятностью  "накрывает" неизвестное значение параметра, т.е.

.

Доверительный интервал для математического ожидания a, в случае нормального распределения с неизвестным средним квадратичным отклонением (точнее, известна только его оценка), имеет вид

,

где t – коэффициент, связанный с распределением Стьюдента и определяемый объемом выборки n и доверительной вероятностью . Коэффициент t обычно находится из таблиц по заданным степеням свободы k=n–1 и доверительной вероятности  (или уроню значимости =1–).

В рассматриваемом случае n=90, следовательно k=89. Тогда, при =0,95, по таблицам для распределения Стьюдента, находим,

.

В результате получаем

.

Отсюда

.

Доверительный интервал для дисперсии , в случае нормального распределения имеет вид

,

где значения чисел и удовлетворяют условиям:

,

и находятся из таблиц для распределения Пирсона. В рассматриваемом случае

, .

Тогда доверительный интервал для дисперсии можно записать в виде

или

.

Доверительный интервал для среднего квадратичного отклонения будет иметь вид

.

Можно построить и симметричный доверительный интервал:

,

где коэффициент q находится из специальных таблиц. В нашем случае

.

Тогда доверительный интервал будет иметь вид

или .

б) Найдем теперь выборочные значения начальных и центральных моментов:

, .

По упрощенному методу, сначала вычисляется центральный момент для новой переменной m_k(u), а затем находят моменты для заданной переменной m_k(x) по формуле

.

Между начальными и центральными моментами существует взаимосвязь:

, .

Здесь нужно иметь в виду, что , .

Найдем начальные моменты по данным таблицы:

, .

Тогда

,

.

Зная моменты 3-го и 4-го порядков, можно вычислить коэффициент асимметрии и эксцесс:

, .

Асимметрия положительна, следовательно, распределение характеризуется незначительной правосторонней асимметрией. Отрицательный эксцесс указывает на более плосковершинное распределение по сравнению с нормальным.

Определим теперь значимость коэффициентов асимметрии и эксцесса. Для этого вычислим погрешность вычислений по формулам

,

.

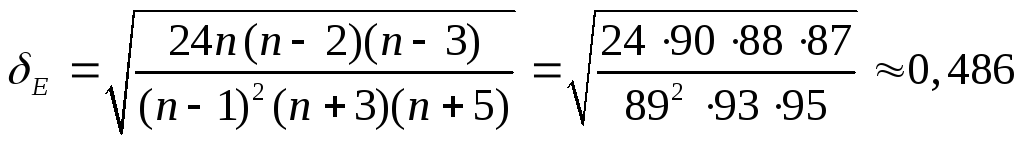Посмотрим теперь, попадают ли найденные значения в "трехсигмовый" интервал:

, .

Из полученных неравенств следует, что коэффициент асимметрии и эксцесс не значимо отличаются от нуля и есть все основания полагать, что распределение генеральной совокупности является нормальным.

в) Критерием согласия называется критерий поверки гипотезы о предполагаемом законе распределения. В соответствии с критерием Пирсона сначала вычисляется величина

,

где p_i – вероятности, полученные по некоторому теоретическому закону распределения. Заметим, что ²-распределение можно применять только при достаточно большом объеме выборки (n50) и достаточно больших частотах (n_i5). Ту группу вариационного ряда, для которых последнее условие не выполняется, объединяют с соседней и, соответственно, уменьшают число интервалов. В рассматриваемом случае мы должны объединить интервалы 1 и 2, а также 9 и 10 (см. таблицу).

i	xi–xi+1	ni
1	582-589	4	–0,4131	–0,4887	0,0756	6,804	0,709
2	589-596	5
3	596-603	6	–0,3159	–0,4131	0,0972	8,748	0,863
4	603-610	12	–0,1700	–0,3159	0,1459	13,131	0,097
5	610-617	21	0,0080	–0,1700	0,1780	16,020	1,562
6	617-624	17	0,1844	0,0080	0,1764	15,876	0,080
7	624-631	9	0,3264	0,1844	0,1420	12,780	1,118
8	631-638	7	0,4192	0,3264	0,0928	8,352	0,219
9	638-645	5
10	645-652	4	0,4898	0,4192	0,0706	0,0706	1,102
		90			0,9785	88,065	5,750

В предположении, что имеет место нормальное распределение, были оценены два параметра этого распределения: и . Если изучаемое распределение подчинено нормальному распределению, то вероятность того, что случайная величина X примет значение из интервала (x_i<X<x_i+1), находится по формуле

,

где – функция Лапласа, значения которой табулированы и приводятся в таблицах. Следует отметить, что функция Лапласа является нечетной функцией, т.е. (–x)=–(x).

Из расчетной таблицы видно, что . Теперь найдем критическое значение . Поскольку у предполагаемой модели были неизвестны оба параметра, поэтому k=2; при расчете критерия использовались восемь интервалов r=8. Таким образом, число степеней свободы =r–1–k=5. При заданном уровне значимости из таблиц для ²-распределения находим

.

Поскольку , то нет оснований отвергать нулевую гипотезу, т.е. что исходное распределение является нормальным.

Построим полигон данного вариационного ряда, а также график плотности предполагаемого нормального распределения:

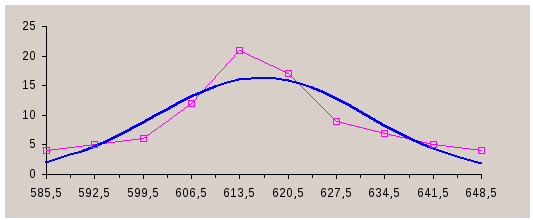
Задание 3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r_xy сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.

X Y	16,24-16,31	16,31-16,38	16,38-16,45	16,45-16,52	16,52-16,59	16,59-16,66	16,66-16,73	16,73-16,80	16,80-16,87	16,87-16,95	ny
582-589								3	1		4
589-596							2		1	2	5
596-603				1		1	2	1		1	6
603-610			1	1		2	4	1	1	2	12
610-617	1			2	7	3	1	7			21
617-624			1	1	6	8	1				17
624-631				2	1	2	1				9
631-638	1	1		2		2	1	3			7
638-645		2	1	1							5
645-652	1	1		2							4
nx	3	4	3	12	14	18	13	15	3	5	90

Решение. а) Количественной оценкой тесноты связи между X и Y является выборочный коэффициент корреляции

,

где . Для вычисления коэффициента корреляции рекомендуется использовать упрощенный метод, поскольку

.

Введем новые переменные , . Запишем корреляционную таблицу для u и v.

u v	–5	–4	–3	–2	–1	0	1	2	3	4	nv
–4								3	1		4
–3							2		1	2	5
–2				1		1	2	1		1	6
–1			1	1		2	4	1	1	2	12
0	1			2	7	3	1	7			21
1			1	1	6	8	1				17
2				2	1	2	1				9
3	1	1		2		2	1	3			7
4		2	1	1							5
5	1	1		2							4
nu	3	4	3	12	14	18	13	15	3	5	90

Вычислим средние значения и средне квадратичные отклонения для величин u и v. Для этого заполним таблицы

ui	ni	ni ui	ni ui2		vi	ni	ni vi	ni vi2
–5	3	–15	75		–4	4	–16	64
–4	4	–16	64		–3	5	–15	45
–3	3	–9	27		–2	6	–12	24
–9	12	–24	48		–1	12	–12	12
–1	14	–14	14		0	21	0	0
0	18	0	0		1	17	17	17
1	13	13	12		2	9	18	36
2	15	30	60		3	7	21	63
3	3	9	27		4	5	20	80
4	5	20	90		5	4	20	100
Сумма	90	–6	408		Сумма	90	41	441

В соответствие с данными таблиц находим средние значения:

,

.

После этого находим дисперсии и средние квадратичные отклонения:

, ,

, .

Однако выборочная дисперсия является несмещенной оценкой, т.е. она дает заниженное значение дисперсии генеральной совокупности, поэтому вместо выборочной дисперсии используют исправленную выборочную дисперсию

.

В данном случае

, .

После этого вычисляем средние квадратичные отклонения для x и y:

, .

Вычислим по данным корреляционной таблицы :

.

Тогда

.

Таким образом, между величинами X и Y существует обратная линейная корреляционная зависимость.

При проведении корреляционного анализа прежде всего возникает вопрос о достоверности корреляционной связи между переменными, т.е. существенно или несущественно отличается коэффициент корреляции от нуля. Другими словами, нужно проверить нулевую гипотезу H₀:r=0 по отношению к альтернативной гипотезе H₁:r0. В качестве критерия проверки нулевой гипотезы принимают случайную величину

.

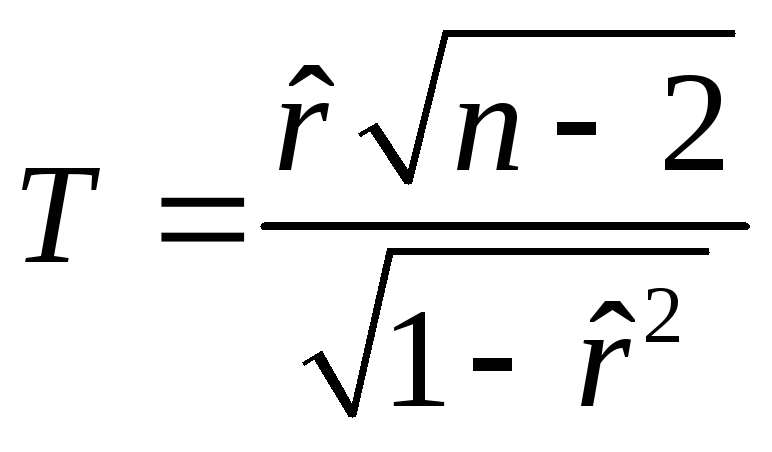Эта случайная величина при справедливости нулевой гипотезы имеет распределение Стьюдента с k=n–2 степенями свободы. Поскольку альтернативная гипотеза имеет вид r0, то критическая область будет двухсторонняя. Так как распределение симметрично относительно оси ординат, то критические точки находят из условия . В результате получается следующее правило определения значимости коэффициента корреляции: а) если , то нет оснований отвергать нулевую гипотезу, т.е. коэффициент корреляции не существенно отличается от нуля; б) если , то нулевая гипотеза отвергается, т.е. коэффициент корреляции существенно отличается от нуля.

Найдем наблюдаемое значение критерия

.

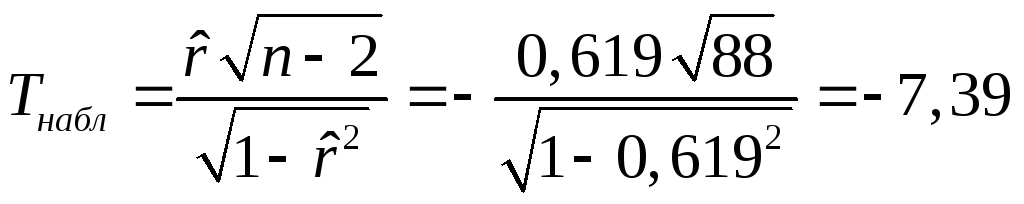Поскольку число степеней свободы k=n–2=88 и 1–/2=0,975, тогда по таблицам для распределения Стьюдента находим

.

Поскольку , то коэффициент корреляции значимо отличается от нуля.

б) Поскольку есть все основания считать, что корреляционная связь является линейной, то уравнения регрессии будут иметь вид

, .

Подставляя найденные уже параметры, получим следующие уравнения линейной регрессии:

.

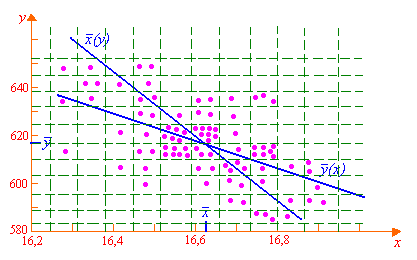
Построим корреляционное поле, для этого разобьем всю плоскость на прямоугольники, в соответствии с интервалами построенных статистических рядов. Каждую точку пару значений из корреляционной таблицы изобразим в виде точки в соответствующей клетке (см. рис.). На этом поле изобразим прямые регрессии. Отметим, что прямые должны пересекаться в точке , в данном случае в точке (16,62; 616,7).

Задание 4. По табличным данным методом наименьших квадратов подобрать функцию . Сделать чертеж.

x	0	2	4	6	8	10	12
y	1080	935	724	362	176	43	19

Решение. В соответствие с методом наименьших квадратов (МНК) следует подобрать коэффициенты a и b таким образом, чтобы функция

приняла минимальное значение. Необходимым условием экстремума функции Q является равенство нулю всех частных производных по неизвестным параметрам. Чтобы упростить вычисления вместо искомой функции рассмотрим ее логарифм

.

Тогда функция Q будет иметь вид

.

Составляем систему уравнений

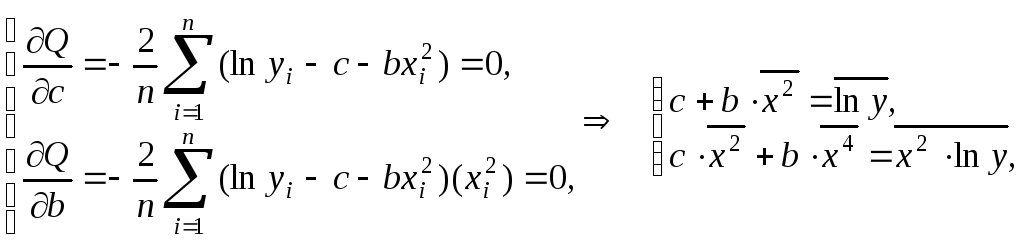
Отсюда находим

и .

Далее, составим таблицу вычислений:

x	y	lny	x2	x4	x2lny
0	1080	6,985	0	0	0,000	1064,3
2	935	6,841	4	16	27,362	947,1
4	724	6,585	16	256	105,357	667,5
6	362	5,892	36	1296	212,099	372,6
8	176	5,170	64	4096	330,911	164,7
10	43	3,761	100	10000	376,120	57,7
12	19	2,944	144	20736	423,999	16,0
6	477	5,454	52	5200	210,836

По данным таблицы находим

, ,

.

Таким образом, искомая функция имеет вид

.

Изобразим на рисунке исходные данные (квадратики) и график искомой кривой:

Задание 5. В таблице приводится зависимость розничного товарооборота (Z, млн. р.) для различных регионов от средней численности населения (X, тыс. р.) и среднегодового дохода (Y, тыс. р.), в расчете на одного человека.

Z	X	Y
1825	1480	2110
814	720	1850
1350	1495	1900
1528	1300	1850
940	1015	1702
862	880	1483
1160	1130	1481
1593	1432	1634
1775	1600	1703
1039	1310	1650
1187	1380	1523

На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.

Решение. Найдем парные коэффициенты корреляции. Для удобства вычислений составим вспомогательную таблицу

Z	X	Y	X2	Y2	Z2	XY	ZX	ZY
1825	1480	2110	2190400	4452100	3330625	3122800	2701000	3850750
814	720	1850	518400	3422500	662596	1332000	586080	1505900
1350	1495	1900	2235025	3610000	1822500	2840500	2018250	2565000
1528	1300	1850	1690000	3422500	2334784	2405000	1986400	2826800
940	1015	1702	1030225	2896804	883600	1727530	954100	1599880
862	880	1483	774400	2199289	743044	1305040	758560	1278346
1160	1130	1481	1276900	2193361	1345600	1673530	1310800	1717960
1593	1432	1634	2050624	2669956	2537649	2339888	2281176	2602962
1775	1600	1703	2560000	2900209	3150625	2724800	2840000	3022825
1039	1310	1650	1716100	2722500	1079521	2161500	1361090	1714350
1187	1380	1523	1904400	2319529	1408969	2101740	1638060	1807801
14073	13742	18886	17946474	32808748	19299513	23734328	18435516	24492574

В результате получим

, , ,

а также

, , .

Отсюда находим

Из таблицы вычисляем

, , .

После этого находим парные коэффициенты корреляции:

Составим корреляционную матрицу

.

Вычислим ее определитель

и алгебраическое дополнение

.

Тогда множественный коэффициент корреляции будет равен

.

Точно такой же результат получается по формуле

.

Величина говорит о том, что теснота связи розничного товарооборота Z от средней численности населения X и среднегодового дохода Y, очень тесная. Совокупный коэффициент детерминации свидетельствует о том, что вариация розничного товарооборота на 89% обуславливается двумя рассматриваемыми факторами.

Вычислим частный коэффициент корреляции

,

поскольку

, , ,

то

.

Аналогичный результат получается по формуле:

.

Вычислим частный коэффициент корреляции

,

поскольку

, , ,

то

.

Аналогичный результат получается по формуле:

.

Сравним частные коэффициенты корреляции с соответствующими парными коэффициентами корреляции:

Видим, что за счет "очищения связи" коэффициенты корреляции изменились незначительно, это связано с тем, что между X и Y существует слабая корреляционная зависимость (r_xy=0,2573). Высокий коэффициент корреляции свидетельствует о сильном влиянии средней численности региона на объем розничного товарооборота, тогда как средний годовой доход на одного человека также влияет на объем розничного товарооборота, но уже не так сильно (), т.е. средняя численность региона оказывает наибольшее влияние на объем розничного товарооборота.

Полагая, что зависимость между исследуемыми факторами линейная, построим уравнение множественной регрессии.

,

где коэффициенты a и b – коэффициенты регрессии, c – параметром,  – величина, характеризующая случайные ошибки. Методом наименьших квадратов можно найти, что

, , .

Подставляя сюда найденные уже значения, получим

, , с=–829,866.

Таким образом, уравнение регрессии будет иметь вид

.