6.3. Геометрическое распределение

Пусть производится стрельба по заданной мишени до первого попадания, при этом вероятность p попадания в цель в каждом выстреле одна и та же и не зависит от результатов предыдущих выстрелов. Другими словами, в рассматриваемом опыте осуществляется схема Бернулли. В качестве случайной величины X будем рассматривать число произведенных выстрелов. Очевидно, что возможными значениями случайной величины X являются натуральные числа: x₁=1, x₂=2, … тогда вероятность того, что понадобится k выстрелов будет равна

. (6.11)

Полагая в этой формуле k=1,2, … получим геометрическую прогрессию с первым членом p и множителем q:

.

По этой причине распределение, определяемое формулой (6.11) называется геометрическим.

Используя формулу суммы бесконечно убывающей геометрической прогрессии, легко убедится, что

.

Найдем числовые характеристики геометрического распределения.

По определению математического ожидания для ДСВ имеем

.

Дисперсию вычислим по формуле

.

Для этого найдем

.

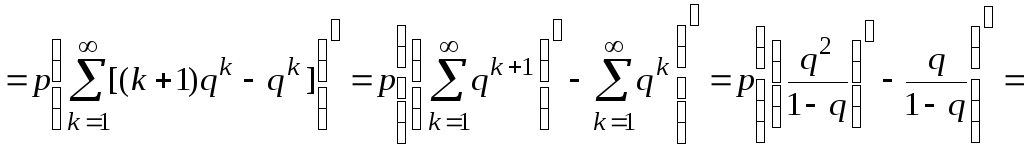
Следовательно,

.

Итак, математическое ожидание и дисперсия геометрического распределения равна

. (6.12)

6.4.* Производящая функция

При решении задач, связанных с ДСВ, часто используются методы комбинаторики. Одним из наиболее развитых теоретических методов комбинаторного анализа является метод производящих функций, который является одним из самых сильных методов и в применениях. Кратко познакомимся с ним.

Если случайная величина  принимает только целые неотрицательные значения, т.е.

,

то производящей функцией распределения вероятностей случайной величины  называется функция

, (6.13)

где z – действительная или комплексная переменная. Отметим, что между множеством производящих функций _(x) и множеством распределений {P(=k)} существует взаимно однозначное соответствие.

Пусть случайная величина  имеет биномиальное распределение

.

Тогда, используя формулу бинома Ньютона, получим

,

т.е. производящая функция биномиального распределения имеет вид

. (6.14)

Добавление. Производящая функция распределения Пуассона

имеет вид

. (6.15)

Производящая функция геометрического распределения

имеет вид

. (6.16)

При помощи производящих функций удобно находить основные числовые характеристики ДСВ. Например, первый и второй начальный моменты связаны с производящей функцией следующими равенствами:

, (6.17)

. (6.18)

Метод производящих функций часто бывает удобен тем, что в некоторых случаях функцию распределения ДСВ очень трудно определить, тогда как производящую функцию порой легко найти. Например, рассмотрим схему последовательных независимых испытаний Бернулли, но внесем в нее одно изменение. Пусть вероятность осуществления события A от испытания к испытанию меняется. Это означает, что формула Бернулли для такой схемы становится неприменимой. Задача нахождения функции распределения в таком случае представляет значительные трудности. Однако для данной схемы легко находится производящая функция, а, следовательно, легко находятся и соответствующие числовые характеристики.

Широкое применение производящих функций основано на том, что изучение сумм случайных величин можно заменить изучением произведений соответствующих производящих функций. Так, если ₁, ₂, …, _n независимы, то

. (6.19)

Пусть p_k=P_k(A) – вероятность "успеха" в k-м испытании в схеме Бернулли (соответственно, q_k=1–p_k – вероятность "неуспеха" в k-м испытании). Тогда, в соответствие с формулой (6.19), производящая функция будет иметь вид

. (6.20)

Пользуясь данной производящей функцией, можем написать

.

Здесь учтено, что p_k+q_k=1. Теперь по формуле (6.1) найдем второй начальный момент. Для этого предварительно вычислим

.

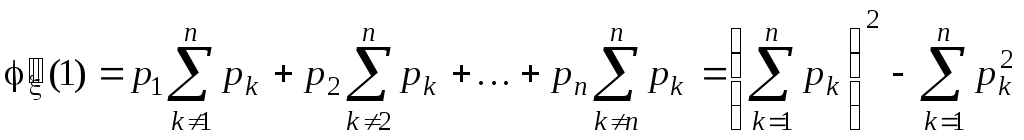Тогда

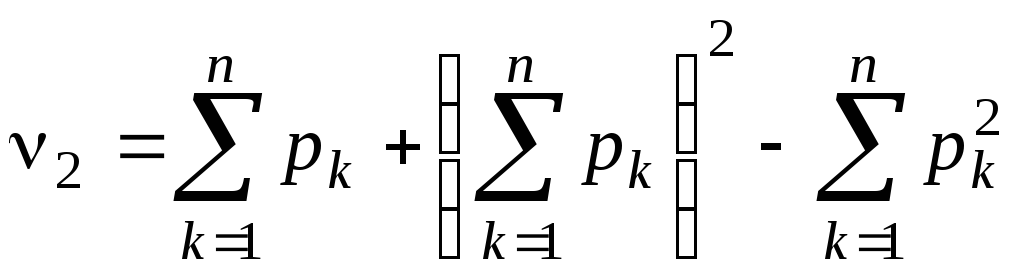и .

В частном случае p₁=p₂=…=p_n=p (т.е. в случае биномиального распределения) из полученных формул следует, что M=np, D=npq.