404 |
13 Multiparticle Systems |
The velocity and acceleration of the center of mass are deÞned in the usual way:
V = |
dR |
, A = |
d2R |
(13.9) |
|
|
. |
dt |
dt 2 |
With these deÞnitions:
Newton’s second law for a system of particles: is system as:
|
d |
|
Fext |
= P = M A . |
(13.10) |
i |
dt |
|
i
where M = i mi and P = pi .
(where we have assumed that the masses of the particles are constant).
This law, Newton’s second law for a system of particles, is what we have been looking for. Equation (13.10) shows that if we deÞne the position of the system in this particular way, we can use NewtonÕs law exactly as we are used to, just remembering that we are not describing the motion of each particle separately, but instead we describe the motion of the effective position R of the system.
This law is powerful and surprisingly beautiful. It is the theoretical justiÞcation for why we do not have to care too much about whether we describe the motion of an object as a point or as a system of particles. We can describe the motion of any system of particles as a point: The center of mass R of the system.
In the next sections we build our intuition about the center of mass R of a system and we learn to apply NewtonÕs second law for a system of particles.
13.2 The Center of Mass
Why do we call the effective position R the center of mass? Let us start by address this in a two-particle system. The effective position, R, of the two-particle system is:
|
|
R = |
|
1 |
(m1r1 + m2r2) |
. |
|
(13.11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
If the two masses are identical, we see that: |
|
|
|
|
R = |
m1r1 |
+ m2r2 |
= |
mr1 + mr2 |
= |
|
1 |
(r1 + r2) , |
(13.12) |
m1 |
+ m2 |
|
2 |
|
|
|
m + m |
|
|
which is the midpoint between the two points.
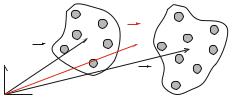
13.2 The Center of Mass
Fig. 13.2 A system consists of two objects A and B. We Þnd the center of mass of the whole system
405
R
y RA
RB
x
We get a similar result for the N -particle system: When all the masses are the same, the effective position R is:
i
as illustrated in Fig. 13.1. This is simply the arithmetic mean of the position vectors. As long as all the masses are the same, the center of mass is what we typically would call the geometric center of the points. What happens when the masses are not equal? In this case, we weigh in the masses in the average, so that the center of mass is the mass-weighed average of the positions of the particles-which is the
natural deÞnition of the center of mass of an object.
Notice that the center of mass R is a vector. We can therefore calculate the center of mass for each component, along each axis, independently of the other axes.
The Subdivision Principle
If we combine two systems A and B, where we know the center of mass for each these systems, how can we Þnd the center of mass for the whole system?
The situation is illustrated in Fig. 13.2. Each of the systems could be a rigid body, or just a collection of point masses. System A has total mass MA and a center of mass at R A , and system B has a total mass MB and center of mass at R B .
Let us enumerate all the particles using the index i . The Þrst k particles are in system A, and the last N − k particles are in system B. What is the center of mass, R, of the whole system with mass M = MA + MB ?
The deÞnition of R is:
|
k |
|
|
N |
|
|
|
|
|
|
M R = |
mi ri = |
mi ri + |
mi ri = MA R A + MB R B , |
(13.14) |
i |
i =1 |
|
|
i =k+1 |
|
and therefore: |
|
|
|
|
|
|
|
|
R = |
MA R A + MB R B |
. |
(13.15) |
|
|
|
|
|
|
|
MA + MB |
|
We can therefore Þnd the center of mass of a system of two objects A and B, by assuming that object A and B are point masses with the whole mass of each object
406 |
13 Multiparticle Systems |
located in the center of mass of each object. This means that if we want to Þnd the center of mass of two solid bodies, we can Þnd the center of mass of each object, and then Þnd the center of mass of the combined object by assuming each object to be a point mass.
Solid Bodies
So far we have only deÞned the center of mass of a system of a Þnite number of particles. How can we Þnd the center of mass of a solid body?
The deÞnition of the center of mass for a continuous object follows directly from the deÞnition for a system of many particles. We divide the solid body into small
volumes Vi = xi yi zi at the position ri . The center of mass is: |
|
|
1 |
|
|
|
|
|
R = |
|
mi ri , |
(13.16) |
M |
i
where the mass of the volume element Vi depends on the local mass density, ρ (ri ). When the size of the volumes goes to zero, the sum approaches the integral of the mass density of the volume, V , of the solid body:
R = |
1 |
(13.17) |
r ρ (r) d V . |
MV
In physics, we often write this as an integral over the mass elements dm instead:
MM
In order to calculate the integral, we calculate the values for each of the components separately:
M X = x ρ (x , y, z) d x d y d z , (13.19)
V
and similarly for the Y and Z components.
13.2.1 Example: Points on a Line
Problem: Find the center of mass R for the system of three particles illustrated in Fig. 13.3.
Solution: We want to determine:
13.2 The Center of Mass
Fig. 13.3 A system of three particles with identical masses, m
a 2a 3a x
Since all the masses are equal, mi = m. We Þnd the x - and y-components independently:
1 |
|
|
|
|
xi = |
1 |
(a + 2a + 3a) = |
1 |
|
6a = 2a , |
(13.21) |
X = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y = |
1 |
yi |
1 |
(a + a + a) = |
1 |
3a = a |
(13.22) |
|
|
|
= |
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The center of mass is therefore: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = 3a i + a j . |
|
|
|
|
(13.23) |
13.2.2 Example: Center of Mass of Object with Hole
Problem: Find the center of mass of a homogeneous disk with radius R, with a circular hole of radius r touching the outer edge of the disk, as illustrated in Fig. 13.4.
Solution: This examples demonstrates that the subdivision principle also can be used in reverse to remove a part of an object, such as a circular hole in a circular disk. We
Fig. 13.4 Illustration of the circular disk of radius R with a circular hole of radius r
y
R
r
x
