4. Метрологическая характеристика среднего результата. Сравнение средних результатов двух выборок

Если с помощью данного метода анализа (измерения) следует определить значение некоторой величины А, то для полученной экспериментально однородной выборки объема m рассчитывают значения величин, необходимые для заполнения табл. 14.1.4.1. Так поступают в том случае, если применяемый метод анализа (измерения) не был ранее аттестован метрологически. Если же этот метод уже имеет метрологическую аттестацию, графы 2, 4, 5, 7, 8 и 9 табл. 14.1.4.1 заполняются на основании данных табл. 14.1.3.1, полученных при его аттестации. При заполнении табл. 14.1.4.1 следует при необходимости учитывать примечания 2.1 и 3.1.

Таблица 14.1.4.1

Метрологические характеристики среднего результата

m	f		s2	s	s	Р	t(P, f)		или
1	2	3	4	5	6	7	8	9	10	11

Таким образом, на основании выражения 2.1 для измеряемой величины А в предположении отсутствия систематической ошибки с вероятностью Р выполняется условие:

, (4.1)

то есть величина А при отсутствии систематической ошибки лежит в пределах:

A = . (4.2)

Примечание 4.1. В случае, предусмотренном в примечании 1.2, в графе 9 табл. 14.1.4.1 приводят величину , а каждую из граф 3, 10 и 11 разбивают на две (а, б). В графе 3а приводят значение , в графе 3б – значение lg , в графах 10а и 106 – соответственно значения нижней и верхней границ доверительного интервала для (см. уравнения 2.11, 2.12). Наконец, в графе 11 приводят максимальное по абсолютной величине значение (см. уравнение 2.12а).

Если в результате измерений одной и той же величины А получены две выборки объема n₁ и n₂, причем , может возникнуть необходимость проверки статистической достоверности гипотезы:

(4.3)

т. е. значимости величины разности ( ).

Такая проверка необходима, если величина А определялась двумя разными методами с целью их сравнения или если величина А определялась одним и тем же методом для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы 4.3 следует установить, существует ли статистически значимое различие между дисперсиями s и s . Эта проверка проводится так, как указано в разделе 3 (см. выражения 3.4, 3.5, 3.5а). Рассмотрим три случая.

1. Различие дисперсий s и s статистически недостоверно (справедливо неравенство 3.5а). В этом случае средневзвешенное значение s² вычисляют по уравнению 1.7, а дисперсию разности – по уравнению 4.4:

(4.4)

. (4.4a)

Далее вычисляют критерий Стьюдента:

, (4.5)

_{при f =} n_{1 +} n₂ –2. (4.5а)

Если при выбранном значении Р (например, при Р = 95 %)

t > t (P, f), (4.6)

то результат проверки положителен – значение ( ) является значимым и гипотезу отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.

2. Различие значений s и s статистически достоверно (справедливо неравенство 3.5). Если s > s , дисперсию s разности ( ) находят по уравнению 4.7, а число степеней свободы ' – по уравнению 4.8:

s = + ; (4.7)

' = (n₁ + n₂ – 2) (0,5 + ). (4.8)

Следовательно, в данном случае

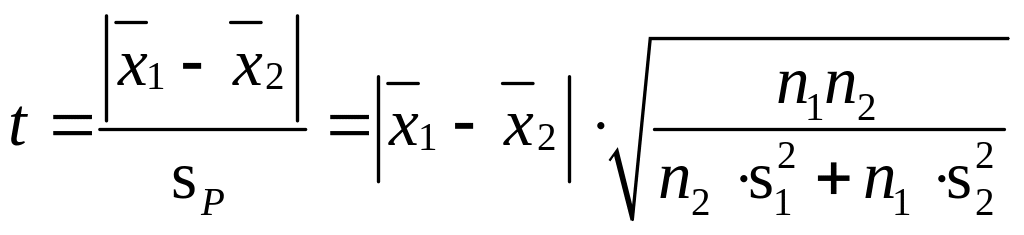. (4.9)

Вычисленное по уравнению 4.9 значение t сравнивают с табличным значением t (Р, f ' ), как это описано выше для случая 1.

Рассмотрение проблемы упрощается, когда n₁ n₂ и s ≫ s . Тогда в отсутствие систематической ошибки среднее выборки объема n₂ принимают за достаточно точную оценку величины А, т. е. принимают = . Справедливость гипотезы = , эквивалентной гипотезе 4.3, проверяют с помощью выражений 3.1, 3.2, принимая f₁ = n₁ - 1. Гипотеза 4.3 отклоняется, как статистически недостоверная, если выполнятся неравенство 3.2.

3. Известно точное значение величины А. Если A = , проверяют две гипотезы: (4.3а) и (4.3б). Проверку выполняют так, как описано в разделе 3 с помощью выражений 3.1 и 3.2 отдельно для каждой из гипотез. Если гипотезы 4.3а и 4.3б статистически достоверны, то следует признать достоверной и гипотезу 4.3. В противном случае гипотеза 4.3 должна быть отброшена.

Примечание 4.2. В случае, предусмотренном примечанием 1.2, при сравнении средних используют величины и .

Когда разность ( ) оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних и :

- t(P, f) (4.10)

Пример 4.1. При определении содержания основного вещества в двух образцах препарата, изготовленных по разной технологии, получены метрологические характеристики средних результатов, приведенные в табл. 14.1.4.2.

Таблица 14.1.4.2

Номер образ- ца	n	f	, %	s2	s	s	Р,%	t(P, f)			,%
1	2	3	4	5	6	7	8	9	10	11	12
1	8	7	99,10	0,25	0,50	0,18	95	2,36	1,18	0,42	0,42
2	6	5	98,33	0,31	0,56	0,23	95	2,57	1,44	0,59	0,60

Требуется решить, является ли первый образец по данному показателю лучшим в сравнении со вторым образцом. Поскольку

F = < F(99 %, 5,7) = 7,46,

то согласно неравенству 3.5а статистически достоверное различие величин и отсутствует. Следовательно, гипотеза = (4.3) проверяется с помощью уравнений 1.7, 1.8, 4.4 и 4.5.

;

s =

;

f = n₁ + n₂ – 2 = 8 + 6 – 2 = 12.

t = 2,72 > t(95 %; 12) = 2,18.

t = 2,72 < t(99 %;12) = 3,08.

Следовательно, с доверительной вероятностью Р = 95 % гипотеза может быть принята. Однако с доверительной вероятностью Р = 99% принять эту гипотезу нельзя из-за недостатка информации.

Если гипотеза принята, то определяют доверительный интервал разности _{генеральных средних и (уравнение 4.10):}

(Р = 95 %; f =12);

_{0,15≤ ≤ 1,39}