Базисное решение задачи лп Симплексный метод решения задач линейного программирования

Симплексный метод – это метод последовательного улучшения плана. Этим методом можно решать задачи линейного программирования с любым количеством переменных и ограничений.

Этот метод включает в себя три основные этапа:

1. Построение начального опорного плана.

2. Правило перехода к лучшему (не худшему) решению.

3. Критерий проверки найденного решения на оптимальность.

При симплексном методе выполняются вычислительные процедуры (итерации) одного и того же типа в определенной последовательности до тех пор, пока не будет получен оптимальный план задачи или станет ясно, что его не существует.

Необходимые условия для применения симплекс-метода:

1. Задача должна иметь каноническую форму.

2. У задачи должен быть явно выделенный базис.

____________________Вопрос 40____________________

____________________Вопрос 41____________________

Графический метод решения задачи лп

1. Построить многоугольник решений системы неравенств

2. Начертить из семейства прямых, соответствующих линейной форме, лини. равных значений функции цели.

Для построения линии равных значений придадим F некоторое числовое значение. Во многих задачах удобно принять, что F=1. Тогда получим c1x1+c2x2=1. Запишем это уравнение прямой в отрезках

Затем, откладывая на оси х1 число 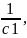а на оси х2 - , найдем точки пересечения линии равных значений с осями координат. Прямая, проведенная через эти точки, и есть требуемая прямая.

3. Двигать прямую вдоль градиента-вектора параллельно линии равных значений в сторону многоугольника решений до соприкосновения с многоугольником решений. Если первая встреча с многоугольником решений произойдет в крайней точке с координатами (x1’, x2’), то в этой точке функция цели достигает минимального значения. Если первая встреча произойдет со стороной многоугольника, то данная функция цели достигает минимума во всех точках стороны.

4. Двигаясь дальше, придем к некоторому опорному положению, когда прямая будет иметь одну общую точку (x1’’, x2’’) с многоугольником решений. В этой точке функция цели достигает своего максимума.

5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения - в вершине, более удаленной от начала координат.

____________________Вопрос 42____________________

Симплекс-метод решения задачи лп

____________________Вопрос 43____________________

Метод искусственных переменных

Расчетные задачи на тестирование

Вычисления Nрасч по заданной точности для методов:

Метод перебора.

Алгоритм оптимального пассивного поиска.

Метод дихотомии.

Метод деления отрезка пополам.

Метод золотого сечения.

Метод чисел Фибоначчи.

Решение:

Метод	Nрасч
М/д перебора	N = Nрасч = {N:N }
Опт. пассивный поиск
М/д дихотомии
М/д деления отрезка пополам
М/д золотого сечения
М/д чисел Фибоначчи

Вычисления расчетной точности Ерасч по заданному N для методов:

Метод перебора.

Алгоритм оптимального пассивного поиска.

Метод дихотомии.

Метод деления отрезка пополам.

Метод золотого сечения.

Метод чисел Фибоначчи.

Метод	Eрасч
М/д перебора	???
Опт. пассивный поиск	N чётное: N нечётное:
М/д дихотомии
М/д деления отрезка пополам
М/д золотого сечения
М/д чисел Фибоначчи
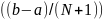