Общая_климатологияКн1

для температуры воздуха, температуры почвы, приходящей солнечной радиации, радиационного баланса, осадков в некоторых частях планеты и других климатических характеристик. Поэтому, если в какой-либо месяц были пропуски наблюдений, то данные для него можно восстановить с использованием этой функции.

На этих двух основных свойствах метеорологических процессов основаны три метода восстановления пропусков и удлинения рядов наблюдений.

Первый из этих методов – метод индивидуальных аналогов является наиболее эффективным и основан на устойчивой во времени синхронности колебаний метеорологической характеристики на рассматриваемой станции и на станции (или станциях) аналоге, близко расположенной и имеющей схожие условия. Ограничением метода является период наблюдений, который должен составлять не менее 6 лет, если рассматривается один аналог и не менее 10 лет, если в уравнении используются два и более аналогов.

Второй метод – метод пространственных моделей или полей основан на однородности метеорологических процессов для больших территорий и наличии пространственного градиента. Этот метод менее эффективен, чем первый, но позволяет восстанавливать временные ряды с продолжительностью наблюдений от 1 года до 6–10 лет.

Третий метод основан на модели сезонной функции, характерной для отдельных метеорологических характеристик и позволяет восстанавливать информацию в одни месяцы по имеющейся информации в другие месяцы на той же самой станции.

Метод индивидуальных аналогов

В методе индивидуальных аналогов вначале выбирается регион, в котором достаточно много предполагаемых пунктованалогов и поэтому площадь данного региона также должна быть достаточно большая, что задается предельным или критическим значением радиуса корреляции Lrad кр, например, равным 600– 800 км. Восстановление пропусков и удлинение временных рядов осуществляется на основе уравнения множественной линейной регрессии вида:

240

где: Y – ряд наблюдений за климатической характеристикой в рассматриваемом пункте, где требуется восстановить пропуски и увеличить продолжительность;

Y1, Y2, … Ym – ряды наблюдений за климатической характеристикой в предполагаемых пунктах-аналогах;

k1, k2, … km, k0 - коэффициенты уравнения регрессии,

m – число пунктов-аналогов в уравнении, при условии, что m < mобщ, где mобщ – общее число выбранных предполагаемых пунктов-аналогов.

Уравнение вида (5.1) является эффективным и может быть применено для восстановления, если оно удовлетворяет следующим условиям:

n’ 6-10, R Rкр, k/ k Bкр , ε/Yp ≤Δ’кр (20-40%), ε/ Y ≤Δкр (20-40%), (5.1)

где n’ – число совместных лет наблюдений в приводимом пункте и пунктах-аналогах;

R – коэффициент парной или множественной корреляции (в зависимости от числа аналогов в уравнении) между значениями климатических характеристик в приводимом пункте и их значениями в пунктах-аналогах;

Rкр – критическое минимальное значение коэффициента парной или множественной корреляции;

k – коэффициенты уравнения регрессии;

k – средняя квадратическая погрешность коэффициента уравнения регрессии;

Bкр – критическое значение отношения k/ k;

ε – среднее квадратическое отклонение остатков уравнения (разностей между фактическими и расчетными значениями);

Y – стандартное (среднее квадратическое) отклонение приводимого к многолетнему периоду ряда;

Yp – восстановленное по уравнению регрессии значение;

241

– предельное значение относительной погрешности восстановленного значения, которая может быть выражена в % при умножении на 100;

кр – предельное значение относительной погрешности восстановленного значения, выраженное через долю СКО не объясненную уравнением регрессии (также выражается в %).

Минимальное число совместных лет наблюдений задается: n’ 6 при одном аналоге, n’ 10 при двух и более аналогах. Общее число аналогов, одновременно включаемых в уравнение (5.1) не должно превышать 3, т. к. при большем числе слагаемых в уравнении уменьшается его статистическая устойчивость, хотя коэффициент множественной корреляции может расти при увеличении числа статистически значимых коэффициентов уравнения. Вместе с тем mобщ может составлять и десятки пунктов-аналогов, но в уравнения, получаемые путем перебора всех аналогов по одному, два и три, будет входить не более трех.

Задать минимальное предельное значение коэффициента корреляции Rкр при котором уравнение еще может считаться эффективным для восстановления можно исходя из двух условий: требуемой погрешности и фактически имеющей место связанности между рядами. Очевидно, что погрешность восстановления следует задавать как можно меньше, но при этом можно не получить ни одного восстановленного значения. Поэтому при задании Rкр следует отталкиваться и от желаемой погрешности и фактически имеющихся условий межрядной связанности. т. е. решать задачу оптимизации. Между погрешностью расчета по уравнению регрессии и коэффициентом корреляции уравнения (R) существует следующее соотношение:

Δ’ = ε2/ Y2, то она будет определяться только коэффициентом корреляции. При R=0,7 погрешность будет равна 1-0,72 = 0,51 или в относительных единицах 51 %, что достаточно много. При

242

R = 0,8 погрешность будет равна 36%, при R = 0,9 погрешность будет 19% и т.д. Желательно, чтобы погрешность была невысокая (не более 30–40%) и поэтому нижнюю границу коэффициента множественной корреляции лучше задать 0,8–0,85. Однако, такая тесная связанность может иметь место далеко не всегда. Так для среднемесячных и среднегодовых температур воздуха при расстоянии несколько сотен километров это условие может еще и выполняется, но для осадков, которые более неоднородны по территории, вряд ли справедливо. Фактически Rкр следует задавать из анализа матрицы парных коэффициентов корреляции или построенной пространственной корреляционной функции. В любом случае Rкр не следует задавать меньше 0,7, чтобы избежать больших погрешностей в восстановленных данных.

Значение Bкр обычно задается равным 2,0, что соответствует 2 -ому интервалу случайной погрешности или 95%-ному доверительному интервалу относительно коэффициента уравнения регрессии km. Если внутри этого доверительного интервала содержится нулевое значение, то аналог с коэффициентом km исключается из уравнения, и оно пересчитывается при другом числе аналогов.

Предельно допустимые относительные погрешности Δ’кр и кр введены для случая большой изменчивости рассматриваемой климатической характеристики, для условий зависимости погрешности от самой величины и чтобы исключить «выбросы» погрешностей. Фактически ε − это СКО погрешности, относящее к среднему значению Y и если Y варьирует в широких пределах, например, для осадков от 10 мм до 200 мм, при среднем значении 50 мм, то ε = 20 мм будет составлять всего 10% для 200 мм, 40% для 50 мм и уже 200% при 10 мм. Чтобы исключить такие большие относительные погрешности для малых значений и вводится Δ’кр не более 40%. Вторая погрешность по отношению к естественной вариации ряда кр используется в тех случаях, когда наблюдаемые величины находятся около нулевых отметок, например, температура воздуха, и делить на саму величину неправильно. Условие допустимых относительных погрешностей Δ’кр и кр позволяет исключить только ненадежно восстановленные отдельные значения, но не само уравнение. Хотя, если все восстановленные значения не

243

будут удовлетворять предельной относительной погрешности, то исключается из дальнейшего рассмотрения и само уравнение.

Уравнения вида (5.1) обычно находятся между рядами одной и той же климатической характеристики на разных станциях. Однако, в частном случае такие регрессионные зависимости могут быть построены и между разными метеорологическими характеристиками на одной станции, например, между температурой воздуха и осадками.

В связи с тем, что априори неизвестны возможные аналоги, то общее число предполагаемых аналогов (mобщ), в соответствии с Lradкр ≤ 400–600 км может быть достаточно большим, а результате перебора всех уравнений с одним, двумя и тремя аналогами общее число уравнений станет намного больше. Так, например, если априори выбрано только 20 предполагаемых аналогов, то общее число всех уравнений будет равно (20•19•18)/(1•2•3) = 1140. Конечно, не все из этих уравнений отвечают условиям эффективности (5.2), но в итоге их все-таки будет достаточно много и по каким из них осуществлять восстановление? Именно для этой цели и разработан алгоритм поэтапного определения восстановленных значений, который состоит в следующем:

-все уравнения, удовлетворяющие условиям эффективности, располагаются в порядке убывания коэффициентов корреляции;

-прежде всего, восстанавливаются погодичные (за каждый год)

значения климатической характеристики по уравнению с наибольшим значением коэффициента корреляции за те годы, в которые есть совместная информация по всем рядам-аналогам, входящим в уравнение;

-далее рассматривается следующее по величине коэффициента корреляции уравнение регрессии и, если с его помощью, получается восстановить еще хотя бы один новый год наблюдений, то оно применяется для восстановления;

-далее рассматривается следующее по величине коэффициента корреляции уравнение и такое поэтапное восстановление погодичных значений продолжается до тех пор, пока не будут использованы возможности всех уравнений регрессии, отвечающие условиям эффективности.

244

В результате ряд восстановленных значений будет получен по разным уравнениям регрессии с разными аналогами, но все эти уравнения будут отвечать условиям эффективности, также, как и полученные по ним восстановленные значения, хотя погрешность восстановленных данных и не будет одинаковой.

Следующая особенность восстановления климатических характеристик связана с тем, что восстановленные данные необходимо корректировать, т. к. их дисперсия искусственно преуменьшена за счет применения метода наименьших квадратом (МНК) при расчете коэффициентов уравнения регрессии. Как было показано в Лекции 3, в МНК минимизируется погрешность только отклика, а факторы считается, что не имеют погрешностей. При установлении же взаимосвязей в гидрометеорологии, погрешности содержатся как отклике, так и в факторах. Поэтому фактически следует для расчета коэффициентов применять не МНК, а однозначную аппроксимацию. Однако для этого метода не разработан математический аппарат в случае многомерного регрессионного анализа. Поэтому коэффициенты уравнений множественной регрессии рассчитываются по МНК, а в расчетные значения вносится поправка с целью увеличить СКО расчетных значений.

На рис. 5.1 показаны зависимости Y = f(X) и X = f(Y) при погрешностях в Y или X соответственно и пунктиром проведена главная диагональ эллипса рассеяния, соответствующая расчету коэффициентов уравнения по методу однозначной аппроксимации. Пересечение всех трех линий находится в точке средних значений Y. Чтобы перейти к этой диагонали от зависимости Y = f(X) необходимо значения Y выше среднего увеличить, а ниже среднего уменьшить. При этом увеличится и наклон линии регрессии и разброс расчетных величин относительно среднего значения, т. е. увеличится СКО.

245

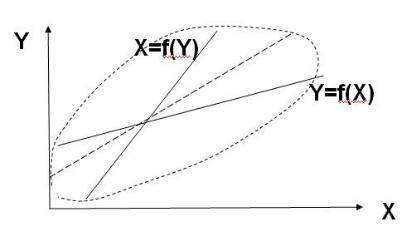
Рис. 5.1. Графическая интерпретация зависимостей, коэффициенты которых получены по МНК и по однозначной аппроксимации

Величина поправки за счет систематического уменьшения дисперсии зависит от разности между расчетным и средним значением и от коэффициента корреляции. В результате корректировка расчетных значений осуществляется по следующей формуле:

где Yip – значения климатической характеристики, полученные по уравнению (5.1) при определении коэффициентов уравнения по МНК,

Yip‘– откорректированное значение климатической характеристики,

Yср – среднее значение климатической характеристики.

Метод, основанный на пространственных моделях

Метод индивидуальных аналогов хотя и является достаточно эффективным, но он не применим, если не выполняются такие условия (5.2), как совместный период n’ > 6–10 лет или фактические коэффициенты корреляции уравнений меньше Rкр = 0,7. Обычно такие ситуации относятся или к очень непродолжитель-

246

ным наблюдениям, или к тем климатическим характеристикам, которые имеют небольшую пространственную связанность. В этом случае можно применять методологию пространственных моделей и связанности полей климатических характеристик. Конечно, такой метод будем менее эффективен, чем метод индивидуальных аналогов, т. к. он основан не на синхронности в ближайших пунктах, а на свойствах всего поля и наличия в нем градиента для рассматриваемой характеристики. При этом связывать между собой можно поля разных лет или поле конкретного года со средним многолетним или климатическим полем. Например, если на какойлибо станции имеются наблюдения только в течение одного j1-го года или даже месяца, то можно построить зависимость между метеорологическими характеристиками за данный год или месяц по многим метеостанциям в регионе и такой же метеорологической характеристикой по многим станциям, но за другой j-ый год, что выражается уравнением простой регрессии:

где Yj1m – наблюдения на всех m метеостанциях региона в j1-ый год, когда имелись наблюдения в рассматриваемом пункте k; Yjm – наблюдения на тех же m метеостанциях региона в j-ый год, в который по (5.5) будет осуществлено восстановление данных в пункте k; b1,b0 – коэффициенты уравнения регрессии.

Поэтому, если имеется даже один год наблюдений, то на основе уравнения вида (5.5) можно восстановить данные в j-ый год, а также и в другие годы, если последовательно связывать поле j1-го года с полями остальных лет, в которые имелись наблюдения на одних и тех же станциях. При этом в качестве критериев эффективности уравнения (5.5) также можно задать предельные минимальные значения числа пунктов в уравнении (m’ 6), коэффициента корреляции (R Rкр = 0,7–0,8), предельной относительной погрешности Δ’кр.< 30–40%. Тогда по зависимости вида (5.5) только на основе одного наблюдения в рассматриваемом пункте в j1-ый год можно восстановить еще столько лет

247

наблюдений, сколько будет получено эффективных уравнений связи между j1-ым годом и другими годами.

Задачу можно несколько усложнить, если в рассматриваемом пункте наблюдения имеются не за один год, а за несколько лет, например, за 2, 3, 4 года. Тогда, как показано на рис. 5.2, для восстановления данных, например, за 1900 год, будет получено не одно уравнение между полем 1900 г. и полем года наблюдений, а

несколько: Y(1900 г.) = f(Y(2009 г.)), Y(1900 г.) = f(Y(2008 г.)),

Y(1900 г.) = f(Y(2007 г.)), …, в связи с тем, что наблюдения на рассматриваемой станции имеются за несколько лет: 2009 г., 2008 г., 2007г., …, т. е. будет иметь место система уравнений для расчета значения в j-ый год:

Yj´=b1´Yj2´+b0´,

Yj´´=b1´´Yj3´´+b0´´,

………………

где Yj, Yj´, Yj´´, … – восстановленные значения в j-ый год, полученные по разным уравнениям связи с полем климатической характеристики за j1-ый, j2-ой, j3-ий и остальные годы, за которые имеют место наблюдений в рассматриваемом пункте.

В результате расчетов по системе уравнений (5.6) в j-ый год будет получено не одно, а несколько восстановленных значений для рассматриваемого пункта, например, k значений. Как выбрать одно из них или обобщить? Есть несколько путей:

248

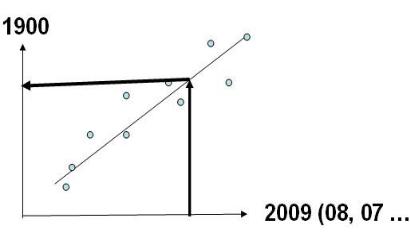
Рис. 5.2. Применение информации нескольких лет наблюдений (2009, 2008, 2007, …) для восстановления данных наблюдений в 1900 г.

методом пространственного моделирования

-выбрать восстановленное значение по наилучшему из уравнений, т. е. тому, которое имеет минимальную остаточную дисперсию

(σ2);

-найти среднее из всех восстановленных значений с учетом весовых коэффициентов, которые будут тем больше, чем меньше остаточная дисперсия, что выражается формулой определения среднего взвешенного восстановленного значения в j-ый год:

где: Yj – средневзвешенное восстановленное значение климатической характеристики в j-ый год в рассматриваемом пункте наблюдений; k – число восстановленных значений в j-ый год в рассматриваемом пункте наблюдений; Yji – восстановленное значений в j-ый год по i-ому году; σji2 – остаточная дисперсия

249