Общая_климатологияКн1

параметр λ тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.

Широкое распространение получило и логарифмически нормальное распределение, которое формируется из нормального распределения путем функционального преобразования случайной величины: x = ey, где x – случайная величина логнормального распределения, y – случайная величина нормального распределения. Поэтому, если случайная величина имеет логнормальное распределение, то ее логарифм имеет нормальное распределение. Случайная величина x при этом является непрерывной и принимает только положительные значения. Иначе логнормальное распределение называют усеченным нормальным распределением по нулевому значению. Графики плотности вероятности логнормального распределения при различных значениях µ и дисперсия σ2 приведены на рис. 3.8.

В отличие от симметричного нормального распределения, логнормальное распределение не является симметричным и имеет скошенность или асимметрию, что связано с наличием нулевого предельного значения. Логнормальное распределение удовлетворительно описывает распределение частот частиц по их размерам при случайном дроблении, например, размеров градин в граде. В климатологии скошенность распределений среднемесячных температур воздуха может иметь место из-за предела тепла или холода. Так, например, распределение температур января в г. Якутске несимметрично в связи с наличием предела самых низких температур (ниже практически некуда), тогда как относительно теплые температуры могут быть различными отдельными затоками тепла, что создает длинный правый «хвост» частотного распределения.

Наибольшее распространение в гидрометеорологии получило гамма-распределение или распределение Пирсона III типа. По определению гамма распределение – это двухпараметрическое семейство абсолютно непрерывных распределений, приведенное на рис. 3.8, где ν – параметр формы, λ – параметр масштаба. Коэффициент скошенности (асимметрии или сдвига) в нем жестко связан со стандартным отклонением (коэффициент асимметрии равен удвоенному коэффициенту вариации Cs = 2Cv), но часто использу-

160

ют и трехпараметрическое представление этого распределения. Плотность трехпараметрического гамма-распределения имеет вид:

где: a – параметр формы , b – параметр масштаба, и с – параметр сдвига, a > 0, b > 0.

Множитель 1/Γ(а) является нормировочным, он введен, что-

бы:

Частным случаем гамма-распределений при а =1 является экспоненциальные распределения (с λ=1/b). При натуральном а и с = 0 гамма-распределения называются распределениями Эрланга. Если случайная величина X имеет гамма-распределение с параметром формы а таким, что d = 2a – целое число, b = 1 и с = 0, то 2Х имеет распределение хи-квадрат с d степенями свободы. Случайная величина X с гамма-распределением имеет следующие характеристики: математическое ожидание М(Х) = ab + c, дисперсию

D(X) = σ2 = ab2, асимметрию равную 2 / 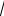a . Нормальное распределение также предельный случай гамма-распределения.

Из наиболее сложных видов аналитических распределений, учитывающих не только центр распределения, разброс относи-

161

тельно центра, асимметрию, но также и пределы изменения случайной величины в каком-либо интервале является бетараспределение (рис. 3.8). Бета-распределение на самом деле больше соответствует природе климатических характеристик, которые должны иметь пределы в существующих на планете квазиоднородных условиях. Так, минимальная зарегистрированная температура на Земле — –89,2°С на антарктической станции “Восток”, и это является практическим нижним пределом, притом для зимних специфических условий изолированного холодного континента. Максимальная же температура на Земле, зарегистрированная в тени, составляет +58°С.

Плотность бета-распределения выражается формулой:

где: α > 0 – коэффициент формы, β > 0 – коэффициент масштаба, A, B – пределы изменения случайной величины x.

Бета-распределение не нашло широкого применения в гидрометеорологии и климатологии из-за того, что для надежного вычисления всех четырех параметров требуются ряды продолжительностью многие сотни лет, которые отсутствуют.

Все рассмотренные распределения являются аналитическими, т. к. получены теоретически с помощью математических выкладок вне привязанности к конкретному объекту исследований. Известным примером физического распределения является распределение молекул по скоростям Джеймса Максвелла, полученное в 1860 г. при помощи статистической механики. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений и к множеству свойств индивидуальных молекул в газе.

В распределении рассматривается общее число n молекул, находящихся в состоянии беспорядочного теплового движения при определенной температуре. После каждого акта столкновения

162

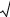
между молекулами, их скорости меняются случайным образом. В результате невообразимо большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным. Найдем в этих условиях, каково число частиц dn из общего числа n имеет скорость в интервале от ν до ν + Δν. Плотность распределения Максвелла имеет вид:

где: m – масса, характеризующая вид газа; Т – температура как параметр состояния.

Как следует из (3.15), в этом распределении статистические показатели связаны с физическими характеристиками. В показателе степени е стоит отношение кинетической энергии, соответствующей данной скорости ν (mν2), к средней энергии теплового движения молекул (2kT). При этом давление Р и объем газа V на распределение молекул не влияют. Поэтому распределение Максвелла характеризует распределение молекул по значениям кинетической энергии, то есть показывает, какова вероятность при данной температуре иметь именно такое значение кинетической энергии.

Известный математик Карл Пирсон (1857–1936) объединил большинство известных аналитических распределений, представленных первыми четырьмя моментами, в виде семейства распределений общего вида (табл. 3.1):

где: a, b0, b1, b2 – параметры.

163

8p(x) k(1 ax ) m , a x 0,0 m 1

9p(x) k(1 ax )m , a x 0, m 1

Семейство распределений Пирсона и близкое к нему семейство Джонсона уже многие десятилетия используются в задачах аппроксимации эмпирических распределений, расчета и оценки вероятностных характеристик. Спектр его применений достаточно широк: в задачах анализа изображений, в моделировании радиоло-

164

кационных сигналов, в оценке рисков, в страховом деле, в регрессионном анализе, в оценке надежности, а также во многих других прикладных задачах теории вероятностей и математической статистики. Существуют также работы и по модификации семейств распределений. Семейства распределений Пирсона и Джонсона сравнимы по своим аппроксимирующим возможностям.

Параметры распределений и их оценка

Параметры распределения – это величины, полностью описывающие какое-либо распределение и входящие в функцию распределения в явном виде. Так, например, нормальное распределение полностью описывают два параметра: среднее значение и дисперсия, распределение Пирсона III типа – три параметра: среднее значение, дисперсия, асимметрия. Значения параметров могут быть определены из теоретических соображений или оценены по выборке, что и осуществляется на практике. По данным наблюдений рассчитываются не точные значения параметров, а приближенные, выборочные. Поэтому говорят, что осуществляется оценка параметров.

Параметры распределения по степени сложности вида распределения делятся на параметры центра распределения, параметр разброса данных относительно центра распределения, параметр скошенности (несимметричности распределения) и параметр плосковершинности распределения.

К параметрам центра распределения относятся: среднее значение, мода и медиана (рис. 3.9 слева). Среднее значение вычисляется как среднее арифметическое по ряду наблюдений. Модой распределения называется наиболее вероятное значение случайной величины: точка максимума плотности распределения. Медиана (по латыни «середина») – это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент.

165

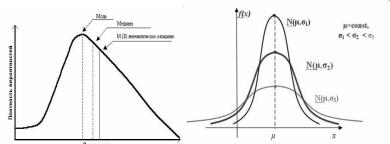
Рис. 3.9. Параметры центра распределения (слева)

иотклонения от центра (справа)

Всимметричном, например, нормальном распределении, все три параметра центра распределения совпадают. Если же распределение несимметрично, как показано на рис. 3.9, то длинный правый «хвост» распределения определяет, что по горизонтальной оси вначале имеет место мода, затем медиана и уже после них – среднее значение. В таких случаях явно асимметричных распределений медиана является более обоснованным показателем центра распределения, чем среднее значение. Наглядным примером может служить распределение доходов населения, когда незначительная часть работающих имеет очень высокие доходы, что искусственно завышает и средний доход для всех остальных. Медиана же дает более правдоподобную картину и не зависит от экстремальных значений в выборке как среднее арифметическое. Часто при статистических обобщениях используется и модальное значение, которое соответствует наиболее часто встречающейся величине в выборке.

Параметр, который характеризует теоретически ожидаемое отклонение случайной величины от ее математического ожидания, называется дисперсией, а квадратный корень из дисперсии – средним квадратическим отклонением (СКО). Как уже отмечалось для нормального распределения, чем больше СКО, тем больше разброс случайной величины и тем меньше вероятность центра распределения (рис. 3.9 справа). Часто требуется сравнивать дисперсии выборок с разными средними, для чего вводится понятие нормированного СКО – коэффициента вариации (Cv), который равен СКО, деленное на среднее значение.

166

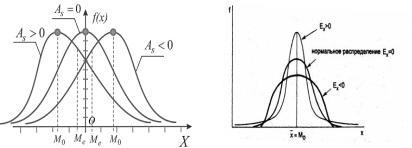
Два других параметра асимметрия и эксцесс характеризуют возможные отклонения от симметричного (нормального) распределения двух видов. В первом случае одна из спадающих ветвей распределения удлинена и распределение скошено или асимметрично. Если удлинена левая ветвь, то говорят об отрицательной или левосторонней асимметрии. Если же удлинена правая ветвь, то асимметрия является положительной и правосторонней (рис. 3.10 слева). Или, иначе: если основная часть распределения в левой стороне, то асимметрию называют положительной и наоборот. Подругому, асимметрия характеризует различие «хвостов» распределения и положительна при более тяжелом правом хвосте и отрицательна при более тяжелом левом хвосте. Для симметричных распределений асимметрия равна нулю.

Рис. 3.10. Параметры асимметрии (слева) и эксцесса (справа)

Второй вид отклонения от симметрии связан с тем, что максимум плотности вероятности расположен выше или ниже, чем у нормального распределения. Если максимум выше и кривая острее, то, эксцесс положительный, при отрицательном эксцессе максимум ниже и распределение более плоское, чем нормальное (рис. 3.10 справа). При эксцессе, равном –2, распределение распадается на два. Можно считать также, кто эксцесс характеризует тяжесть хвостов распределения: положительные значения эксцесса соответствуют распределениям с более тяжелыми хвостами, чем у нормального распределения.

Оценки параметров распределения, как и любые получаемые по выборке статистики, должны удовлетворять следующим четырем условиям.

167

1)Оценки параметров должны быть несмещенными (unbiased), т. е. при очень большом числе испытаний среднее значение оценок должно стремиться к истинному значению генеральной совокупности. Если этого нет, то оценка смещена и смещение (bias) может быть обусловлено ошибками измерений и другими причинами. Такие ошибки называются систематическими и приводят к завышению или занижению оценки.

2)Оценки должны быть состоятельными или согласованными, т. е. с ростом объема выборки они должны стремиться к соответствующему параметру генеральной совокупности.

3)Оценки должны быть эффективными (efficient), т. е. для выборок равного объема они должны иметь минимальное рассеяние и дисперсию.

4)Оценки должны быть достаточными (sufficient), т. е. не должна возникать необходимость в дополнительной информации об оцениваемом параметре и статистика должна содержать всю основную возможную информацию.

Три из этих условий (состоятельность, эффективность, достаточность) были введены Р.А. Фишером в 1925 г.

Для оценки параметров по выборочным данным разработаны многочисленные методы и среди них особое значение имеет метод максимального правдоподобия, предложенный Р. Фишером в 1912 г. Это универсальный метод оптимального оценивания неизвестных параметров, применяемый в случаях, когда вид функции распределения известен. В этом методе оценки неизвестных параметров равны значениям, при которых полученная выборка имеет максимальную вероятность появления, т. е. в качестве оценок отыскиваются значения, максимизирующие функцию максимального правдоподобия для параметров, в предположении, что эти параметры существуют. Этот метод построения точечных оценок параметров находится в тесной связи с методом наименьших квадратов. Оценки, полученные методом максимального правдоподобия, являются состоятельными, асимптотически эффективными, но их несмещенность требует проверки.

Так, например, для нормального закона распределения функция максимального (наибольшего) правдоподобия для выборки объемом n имеет следующий вид:

168