ТВ и МС 2013 экономика

3. Разбор типовых задач

Пример 3.1. Дано 5 карточек с буквами К, М, Р, О, Я. Найти вероятность того, что:

а) наугад выбранные и разложенные в ряд одна за другой три карточки образуют слово РОМ;

б) при случайном расположении в ряд всех пяти карточек получится слово МОРЯК.

Решение. а) Пусть события А – при выборе трех карточек получится слово РОМ. Различные комбинации трех букв из имеющихся пяти представляют собой размещения [1, стр. 27], так как могут отличаться как составом входящих букв, так и порядком их следования, или и тем, и

другим. Общее число таких размещений, а значит, и число исходов

классическому определению вероятности [1, стр. 16], вероятность события А будет равна:

Р A mn 601 0,017 .

б) Пусть событие В – при случайном расположении в ряд всех пяти карточек получится слово МОРЯК. Различные комбинации из имеющихся пяти букв представляют собой перестановки [1, стр. 27], так как отличаются друг от друга только порядком следования букв. Таким образом, общее число исходов этого эксперимента равно числу перестановок из пяти букв,

т.е. n P 5!=120. Число исходов, благоприятствующих событию В,

5

составляет m 1. Поэтому

Р B mn 1201 0,0083 .□

10

Пример 3.2. Дано 6 карточек с буквами. На трех из них написана буква

А, на двух – буква Н и на одной буква С. Найти вероятность того, что при расстановке всех букв в ряд получится слово АНАНАС.

Решение. Пусть событие А – получилось слово АНАНАС. В отличие от примера 1, здесь буквы в слове повторяются. Поэтому число всевозможных случаев будет определяться числом перестановок с повторениями:

Пример 3.3. В классе учатся 10 юношей и 15 девушек. Для дежурства случайным образом отобраны три школьника. Найти вероятность того, что все дежурные окажутся юношами.

Решение. По условию задачи испытание состоит в том, что для дежурства производится выбор трех учащихся из их общего количества,

равного 25. В нашем случае, когда фамилии дежурных не важны, а важен лишь их пол, все исходы такого эксперимента будут представлять собой полную группу событий, которая может быть представлена схематично

(Рис. 3.1). Суть представленной схемы следующая.

В классе всего 25 человек, среди которых 10 юношей и 15 девушек

(верхняя строка схемы). В результате испытания из 25 человек отбирают троих (в нижних строках столбец по центру). Среди этих трех человек может встретиться от 0 до 3 юношей (левый столбец нижних строк) и, наоборот, от

3 до 0 девушек (правый столбец нижних строк). Так, например, если юношей отобрано трое, то формально можно сказать, что девушек отобрано нуль (на схеме это событие выделено цветом). Рассуждая аналогично, получаем все остальные возможные исходы данного испытания.

11

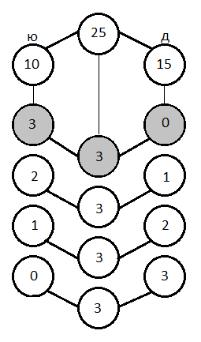
Заметим, что такие события в данном случае не являются равновозможными, но их вероятности могут быть найдены с помощью комбинаторики.

Рис. 3.1

Поскольку порядок выбора учащихся не важен, то имеем дело с сочетаниями без повторений [1, стр. 28], т.е., общее число таких равновозможных исходов данного испытания – это число сочетаний из 25

по 3:

Событие А – среди отобранных дежурных только юноши – на схеме выделено цветом и наступает тогда и только тогда, когда из 10 юношей выберут трех, а из 15 девушек - ни одной. Согласно правилу произведения [1,

стр. 25], для подсчета числа благоприятных исходов нужно перемножить число сочетаний из 10 по 3 и из 15 по 0:

12

При подсчете применили свойство числа сочетаний, а именно Cn0 1.

Далее, согласно классическому определению вероятности, искомая вероятность:

Вероятность выигрыша по одному билету составляет 0,2. Найти вероятность того, что студент выиграет:

а) по трем лотерейным билетам;

б) не менее чем по трем билетам;

в) хотя бы по одному билету.

Определить наивероятнейшее число выигрышных билетов.

Решение. Испытание состоит в проверке билета на выигрыш. По условию число таких испытаний составляет n 5 . В каждом испытании

наступает или не наступает событие А – проверяемый билет содержит выигрыш. Очевидно, что наступление события А в каждом предыдущем

испытании не изменяет его вероятности в последующих и, следовательно,

испытания являются независимыми. При этом, вероятность наступления события А в каждом испытании постоянна и равна p 0,2, и, таким образом,

вероятность того, что событие А не наступит, равна q 1 p 1 0,2 0,8 .

На основании вышесказанного можно сделать вывод о том, что мы имеем дело с повторными независимыми испытаниями, и при решении задачи можно использовать формулу Бернулли [1, стр. 50].

а) Пусть событие В – студент выиграл по трем лотерейным билетам.

Следовательно, число испытаний, в которых ожидается наступление события

А, равно m 3 . Искомую вероятность найдем по формуле Бернулли:

б) Пусть событие С – студент выиграл не менее чем по трем лотерейным билетам. Такому событию благоприятствуют три случая:

13

событие А наступает три, четыре или пять раз. Все эти события

несовместны, поэтому, согласно теореме сложения вероятностей несовместных событий, вероятность суммы несовместных событий будет равна сумме вероятностей каждого события, включенного в сумму, т.е.

имеем:

в) Пусть событие D – студент выиграл хотя бы по одному лотерейному билету. Выиграть хотя бы по одному билету означает выигрыш либо по одному, либо по двум, либо по трем, либо по четырем или, наконец,

по пяти билетам, т.е. событие D представляет сумму всех этих несовместных событий. Поэтому, здесь также можно было бы воспользоваться теоремой сложения вероятностей несовместных событий. Но достаточно большое число слагаемых делает расчет весьма громоздким, и чтобы избежать этого,

проще перейти к противоположному событию D – все билеты без выигрышей. Для такого события число испытаний, в которых ожидается наступление события А, равно m 0. На основании формулы, связывающей вероятности противоположных событий, вероятность искомого события будет равна:

P D 1 P D 1 P0,5 1 C50 p0q5 1 0,85 0,67232 .

Наиболее вероятное число успехов m0 удовлетворяет следующему двойному неравенству:

целую часть числа х.

В нашем случае наивероятнейшее число выигрышных билетов будет равно:

m0 np p 5 0,2 0,2 1,2 1 . □

14

Пример 3.5. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 200 договоров

с выплатой страховой суммы будет связано:

а) 20 договоров;

б) наивероятнейшее число договоров;

в) от 25 до 45 договоров включительно;

г) не более 40 договоров;

д) от 25 до 35 договоров.

Решение. Очевидно, что здесь имеют место повторные независимые

испытания. Каждое испытание связано с наступлением или не наступлением

q P A 1 p 1 P A 1 0,15 0,85 . Так как число испытаний n 200

достаточно велико, применять здесь формулу Бернулли нецелесообразно, и

надо воспользоваться асимптотическими формулами. В частности,

выполнены все условия применимости локальной и интегральной теорем Муавра-Лапласа [1, стр. 53], ибо число испытаний n 200 достаточно велико и npq 200 0,15 0,85 25,5 20.

а) Согласно локальной теореме Муавра-Лапласа, вероятность того, что событие А появится в n независимых испытаниях ровно m раз, приближенно

определяется по формуле:

искомого события:

15

в) Согласно локальной теореме Муавра-Лапласа, вероятность того,

что число m наступлений события А в n повторных независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе испытаний n приближенно равна

При вычислении воспользовались нечетностью функции Лапласа и таблицей значений функции Лапласа [1, Приложение II, стр. 199].

16

в) Необходимо найти P200 m 40 . Так как число договоров не может

быть отрицательным, то определение последней вероятности эквивалентно

достаточно большом числе n независимых испытаний вероятность того, что

Пример 3.6.* По статистическим данным известно, что в некоторой местности в среднем на каждые 100 семей приходится 30 автомобилей.

1. Найти вероятность того, что из 1000 семей доля имеющих автомобиль:

а) будет заключена в пределах от 0,28 до 0,33;

17

б) будет отличаться от вероятности этого события не более чем на 0,02

которому при достаточно большом числе n независимых испытаний вероятность того, что доля m/n появлений события А заключена в пределах от

до (включительно) определяется соотношением:

Тогда:

18

испытаний вероятность того, что доля m/n появлений события А отличается от ее вероятности р не более, чем на положительную величину 0 (по абсолютной величине), определяется соотношением:

Таким, образом, найдем:

Заменяя левую часть неравенства согласно следствию из интегральной теоремы Муавра-Лапласа для доли функцией Лапласа, приходим к следующему соотношению:

Воспользовавшись таблицей значений функции Лапласа, определяем ее аргумент, соответствующий значению функции, равному 0,9545. По таблице получаем, что аргумент равен 2, т.е.:

19